振動・波動の基礎-⑩2自由度系の非減衰強制振動と反共振点

2自由度の自由振動は複雑な動きするのがわかったけど、強制振動も複雑なの

苦手君

デルタ先生

厳密には複雑なんだけど、重要な現象を単純に理解するだけで大丈夫なことも多いよ。

本記事では、2自由度の非減衰の強制振動について解説します。

前回までで、2自由度の自由振動について解説しましたが、自由振動に周期的な外力が発生した場合にどのような動きをするか、イメージできるようになりましょう。

1自由度の強制振動については、下記で解説していますので、参考にしてくださいね。

参考記事

本記事をおススメする人

2自由度の強制振動を理解したい人
物理を勉強していて興味がある人、仕事で振動の知識を使う人

今回は、2つの質点にそれぞれ外力を与えたケースを考えますね。

1 質点$m_1$に外力を与えた場合
2 質点$m_2$に外力を与えた場合
3 まとめ
4 参考文献

質点$m_1$に外力を与えた場合

動画でも解説していますので、下記の動画を参考にしてください。

モデル

質点$m_1$に外力を与えた場合、これまでのモデルに外力を付け加えた形になります。

今回は質点$m_1$に外力$f_1(t)$を付け加えましょう。

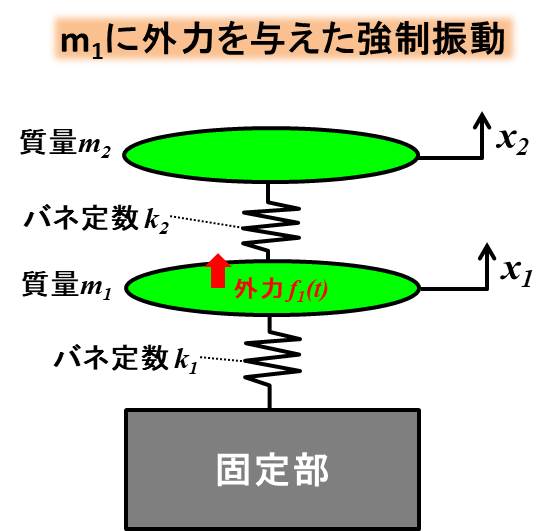
非減衰なので、減衰のダンパーはつけておりません。

バネで2つの質点がつながっている状態ですね。

運動方程式

運動方程式は自由振動に外力を加えるだけです。

過去の記事で2自由度の自由振動についての運動方程式を解いていますので、こちらを参考にしてくださいね。

参考記事

自由振動の運動方程式は下記です。

$$\left(\begin{array}{cc}m_1&0\\0&m_2\end{array}\right)\left(\begin{array}{c}\ddot{x_1}\\\ddot{x_2}\end{array}\right)+\left(\begin{array}{cc}k_1+k_2&-k_2\\-k_2&k_2\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right)=\left(\begin{array}{c}0\\0\end{array}\right)$$

質点$m_1$における方程式の右辺に、$f_1(t)=Fcosωt$を付け加えます。

連立方程式の形で書けば下記になりますね。

$$m_1\ddot{x_1}+(k_1+k_2)x_1-k_2x_2=Fcosωt・・・①$$

$$m_2\ddot{x_2}-k_2x_1+k_2x_2=0・・・②$$

以上が運動方程式になります。

1自由度系と考え方は同じで、外力を付け加えただけですね。

運動方程式の解き方

さて、それでは実際の動きを見るために、運動方程式を解いていきましょう。

$m_1$の運動方程式は、1自由度の時と同じで、非斉次の微分方程式です。

これが連立しているので、非斉次の連立微分方程式の解法を考えます。

連立方程式とはいえ、解き方としては1自由度のときと大きく変わりません。

1自由度のときの解き方の詳細は、過去記事を参考にしてください。

非斉次の微分方程式の一般解は、下記のような形で表されるのでしたね。

一般解＝斉次方程式の一般解 + 非斉次方程式の特解

斉次方程式というのは、1自由度のときと同じで、 自由振動のときの運動方程式です。

自由振動のときの一般解は、前回の記事で求めていますので、 非斉次方程式の特解を求めてしまえば、強制振動のときの一般解が求まりますね。

運動方程式を解く

特解をもとめるだけでよいので、特解を求めましょう。

強制振動の特解を仮定するのですが、2回微分した微分方程式は三角関数で置くと上手くいくことが多いのでしたね。

特解を次のように仮定します。

$$x_1=X_1cosωt、x_2=X_2cosωt$$

今回、強制振動ですので、ωは既知とします。

つまり、与える外力の周波数はすでにわかっています、ということです。

運動方程式に代入する必要があるので、先に特解を2回微分しておきます。

$$\ddot{x_1}=-ω^2X_1cosωt、\ddot{x_2}=-ω^2X_2cosωt$$

さて、下記の運動方程式に代入しましょう。

$$m_1\ddot{x_1}+(k_1+k_2)x_1-k_2x_2=Fcosωt・・・①$$

$$m_2\ddot{x_2}-k_2x_1+k_2x_2=0・・・②$$

①式に特解を代入すると、

$$-m_1ω^2X_1cosωt+(k_1+k_2)X_1cosωt-k_2X_2cosωt=Fcosωt$$

$cosωt$を消去できて、

$$-m_1ω^2X_1+(k_1+k_2)X_1-k_2X_2=F・・・③$$

次に②式に特解を代入すると

$$-m_2ω^2X_2cosωt-k_2X_1cosωt+k_2X_2cosωt=0$$

これも$cosωt$が消去できるので、

$$-m_2ω^2X_2-k_2X_1+k_2X_2=0・・・④$$

③と④の連立方程式を解くことで、$X_1$と$X_2$が求まります。

ちょっと面倒ですが、力づくで連立方程式を解いてみましょうか。

連立方程式の$X_1$、$X_2$の係数を$A、B、C、D$と置きます。

$A=-m_1ω^2+k_1+k_2、B=-k_2、C=-k_2、D=-m_2ω^2+k_2$とすると、

$$AX_1+BX_2=F$$

$$CX_1+DX_2=0$$

この連立方程式の解は、

$$X_1=\frac{F・D}{AD-BC}・・・⑤$$

$$X_2=\frac{-F・C}{AD-BC}・・・⑥$$

となります。

ここで、$AD-BC$についてですが、これは自由振動の計算の際に、計算されております。

$F=0$とすると、もとの方程式は、

$$(-ω^2m_1+k_1+k_2)X_1-k_2X_2=0$$

$$-k_2X_1+(-ω^2m_2+k_2)X_2=0$$

これらを行列表記すると、

$$\left(\begin{array}{cc}-ω^2m_1+k_1+k_2&-k_2\\-k_2&-ω^2m_2+k_2\end{array}\right)\left(\begin{array}{c}X_1\\X_2\end{array}\right)=0$$

1次従属となる条件から、

$$det\left[\begin{array}{cc}-ω^2m_1+k_1+k_2&-k_2\\-k_2&-ω^2m_2+k_2\end{array}\right]=0$$

この行列式をは、下記のようになります。

$$(-ω^2m_1+k_1+k_2)(-ω^2m_2+k_2)-k_2^2=0$$

$ω^2$の式に変形して、

$$m_1m_2ω^4-{(k_1+k_2)m_2+k_2m_1}ω^2+k_1k_2=0$$

この式は、$AD-BC=0$と一致しています。

この時の解を1次と2次の固有振動モードの振動数$ω_1$、$ω_2$として、

$$ω_{1,2}=\sqrt{\frac{1}{2}\biggl\{\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2}±\sqrt{(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2})^2-\frac{4k_1k_2}{m_1m2}}}\biggr\}$$

ただし$ω_1<ω_2$です。

$AD-BC=0$はωの4次方程式で、解が$ω_1$と$ω_2$の解なのですから、下記のように因数分解できます。

$$AD-BC=m_1m_2ω^4-{(k_1+k_2)m_2+k_2m_1}ω^2+k_1k_2=m_1m_2(ω^2-ω_1^2)(ω^2-ω^2_2)$$

⑤と⑥式の$AD-BC、C、D$に値を入れて、書き直すと、

$$X_1=\frac{(-m_2ω^2+k_2)F}{m_1m_2(ω^2-ω_1^2)(ω^2-ω^2_2)}$$

$$X_2=\frac{k_2F}{m_1m_2(ω^2-ω_1^2)(ω^2-ω^2_2)}$$

このようにスッキリとした形になります。

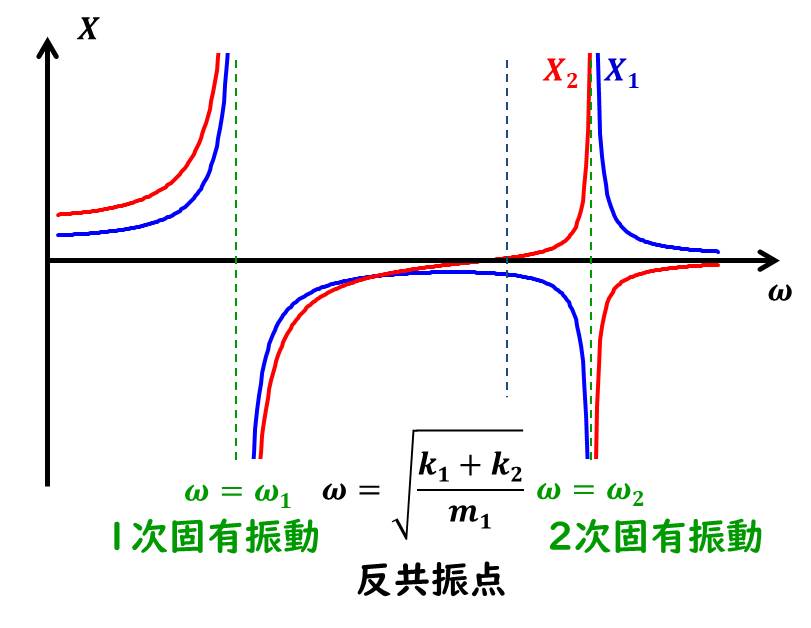
周波数に対しての挙動

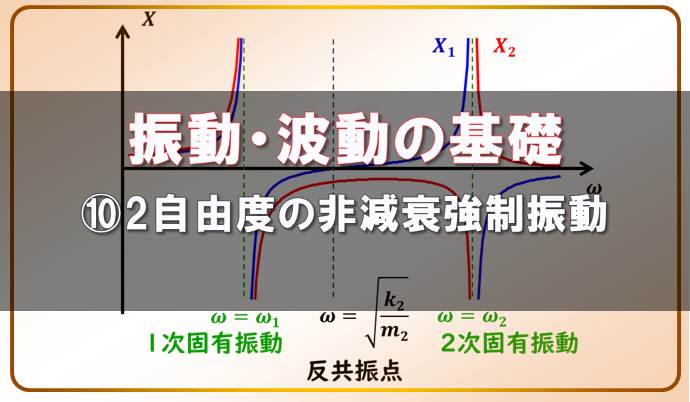
それでは、外力の周波数ωに対して、各質点の振幅はどのようになるのかについて、グラフを見てみましょう。

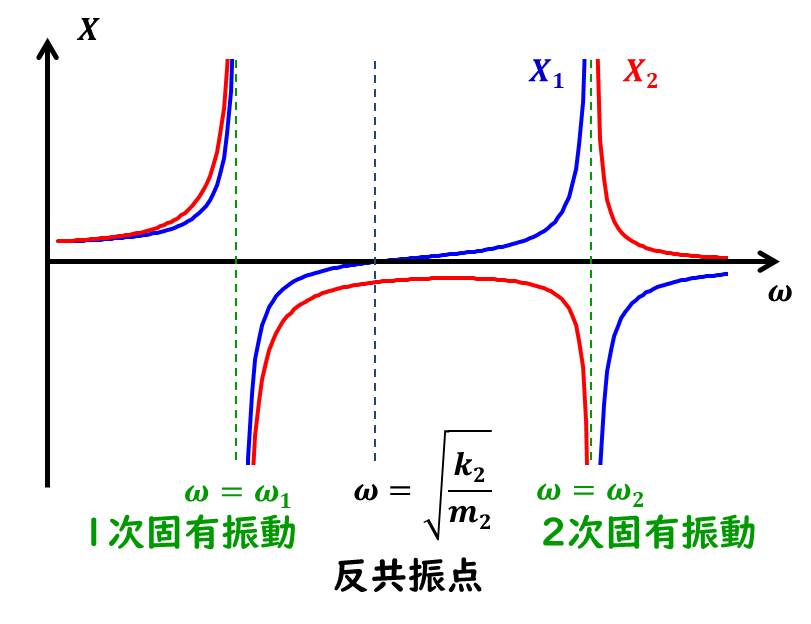
$X_1$、$X_2$ともに分母に$((ω^2-ω_1^2)(ω^2-ω^2_2)$がありますので、$ω=ω_1$や$ω=ω_2$のときに、∞になりますね。

減衰がない場合、$ω_1$や$ω_2$の振動数の外力を加えると、共振して振幅は無限大になる、というのは1自由度のときと同じです。

また、$X_1$の分子に注目すると、$ω=\sqrt{\frac{k_2}{m_2}}$のときに、ゼロになります。

この状態だと、質点$m_1$が全く振動していません。

このときの振動数を 反共振点、と呼びます。

質点$m_2$に外力を与えた場合

こちらについては下記の動画の前半で解説していますので参考にしていただければと思います。

モデル

これまでと同様に、$m_2$に外力を与えた場合を考えてみましょう。

この場合のモデルは下記です。

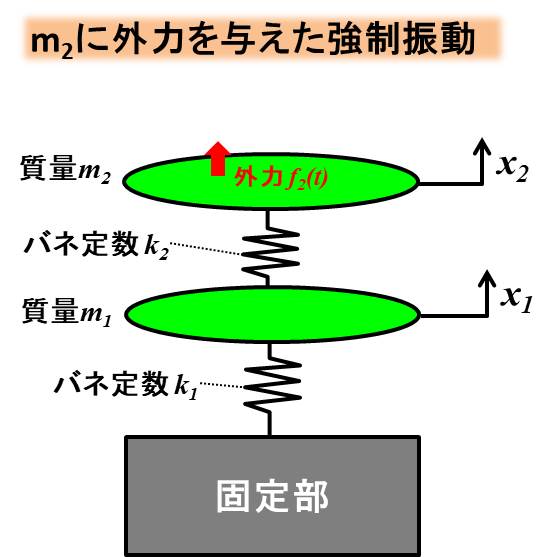
上側の質点$m_2$に外力を与えています。

運動方程式

$$m_1\ddot{x_1}+(k_1+k_2)x_1-k_2x_2=0・・・⑦$$

$$m_2\ddot{x_2}-k_2x_1+k_2x_2=Fcosωt・・・⑧$$

下側の方程式の右辺に外力の項が付け加わりました。

$x_1=X_1cosωt、x_2=X_2cosωt$と特解を仮定して、2回微分したものを計算すると、

$$\ddot{x_1}=-ω^2X_1cosωt、\ddot{x_2}=-ω^2X_2cosωt$$

これらを⑦、⑧に代入して、$cosωt$を消去すると、

$$-m_1ω^2X_1+(k_1+k_2)X_1-k_2X_2=0・・・⑨$$

$$-m_2ω^2X_2-k_2X_1+k_2X_2=F・・・⑩$$

$m_1$に外力を与えた場合と同じように、方程式の係数を$A、B、C、D$と置くと、

$$AX_1+BX_2=0$$

$$CX_1+DX_2=F$$

この連立方程式を解くと、

$$X_1=\frac{-B・F}{AD-BC}$$

$$X_2=\frac{A・F}{AD-BC}$$

$AD-BC$については、$m_1$に外力を与えた場合と同じように、1次、2次の固有振動モードの振動数を使って書き換えれるので、下記のようになります。

$m_2$に外力を与えた場合

$$X_1=\frac{k_2F}{(ω^2-ω_1^2)(ω^2-ω^2_2)}$$

$$X_2=\frac{(-m_1ω^2+k_1+k_2)F}{m_1m_2(ω^2-ω_1^2)(ω^2-ω^2_2)}$$

上の式と下記の$m_1$に外力を与えた場合の式を比較してみましょう。

$m_1$に外力を与えた場合

$$X_1=\frac{(-m_2ω^2+k_2)F}{(ω^2-ω_1^2)(ω^2-ω^2_2)}$$

$$X_2=\frac{k_2F}{m_1m_2(ω^2-ω_1^2)(ω^2-ω^2_2)}$$

$X_1$と$X_2$が入れ替わって、形はよく似ていますね。

グラフを見てみましょう。

グラフも$X_1$と$X_2$が入れ替わっただけでそっくりですね。

相違点

そっくりだけど、少し違う気がするんだけど・・・

苦手君

デルタ先生

そうだね、実は質点につながっているバネの本数の違いで、反共振点が少しずれるんだ。

縦に並べて比較して見ましょう。

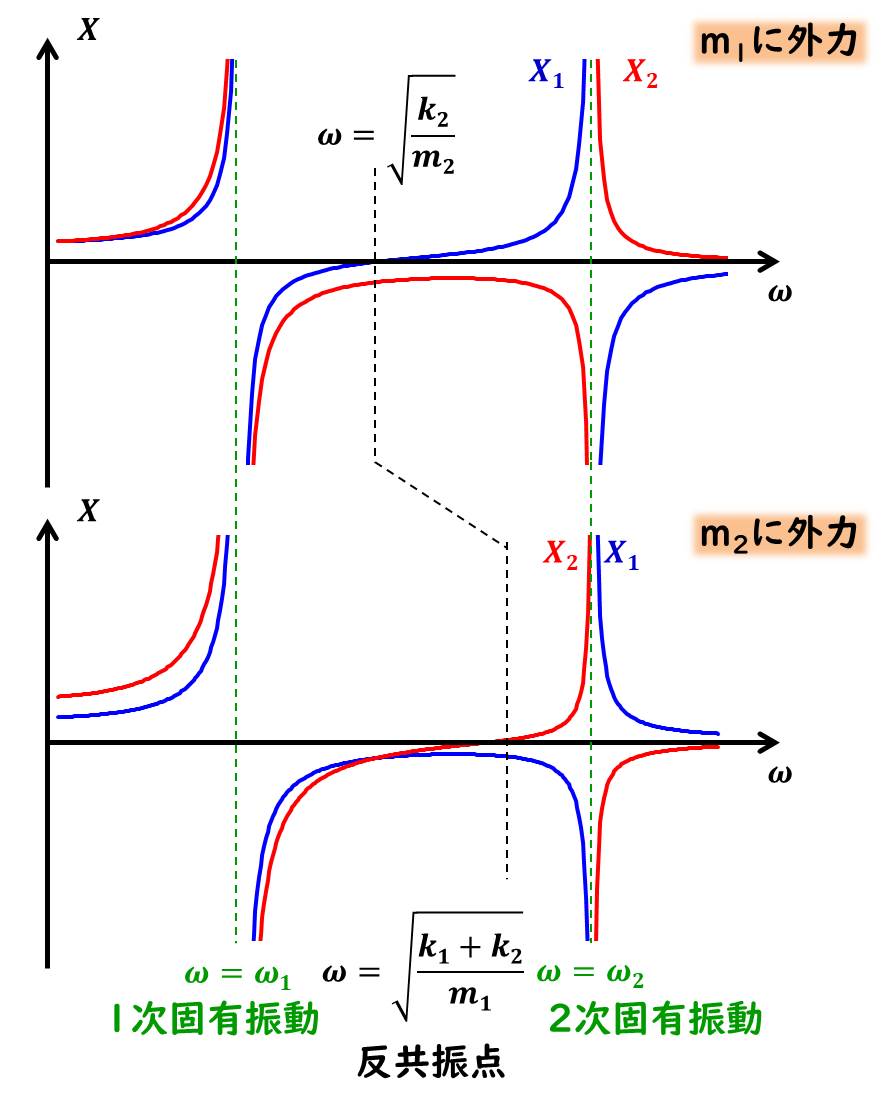
反共振点の振動数が異なっていますね。

反共振点での振動は、力をかけた質点と別の質点が動く振動であり、動く質点につながっているバネの本数で反共振点の位置が変わってしまうのです。

質点$m_1$に力をかけて質点$m_2$を動かす場合、質点$m_2$につながっているバネは$k_2$の1本ですね（下図の赤のバネが$m_2$につながっているバネで、本数は1本）

逆に質点$m_2$に力をかけて質点$m_1$を動かす場合、質点$m_1$につながっているバネは$k_1$と$k_2$の2本ですね。（下図の赤のバネが$m_1$につながっているバネで、本数は2本）

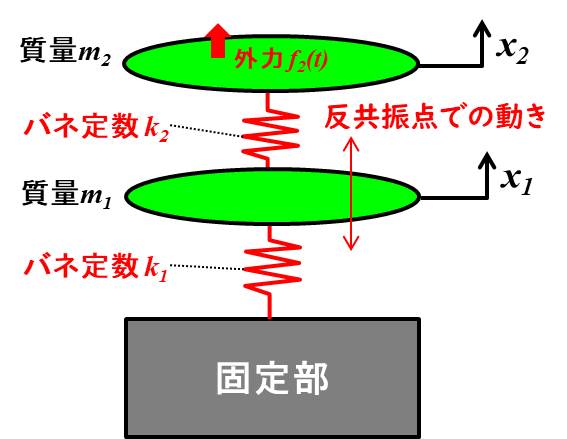
バネが2本つながっているため、$m_1$を動かすための力が増えるイメージです。

その他の特解の取り扱いについて

今回、$f=Fcosωt$と特解を設定しましたが、$sinωt$や、$cos(ωt+δ)$と置いた場合、どうなるのか、ということについてです。

結論、$cosωt$のときと同じ挙動になります。

なぜならば、運動方程式に特解を代入すると、三角関数の成分は消去されるためです。

まとめ

2自由度の非減衰強制振動について解説しました。

$m_1$に外力を与えた場合、$m_2$に外力を与えた場合の2通りを解説し、その違いについても説明しました。

共通点として、 固有振動モードの振動数で共振現象が起こり、 減衰が無いため振幅が無限大に発散することを数式とグラフで確認しました。

また、1次と2次の固有振動モードの間に反共振点という振動数が存在し、ここでは、 外力を与えた質点は動かないが、他方の質点が振動する、という現象が起こります。

外力を与える質点を変えることで、反共振点の振動数が異なりますが、これは質点に繋がれているバネの本数が異なることが理由でした。

最後に、運動方程式を解くときに、特解を$f=Fcosωt$としましたが、$sin$でも$cos(ωt+δ)$でも結果は同じ、ということを補足しております。

ここまで理解できれば、2自由度の非減衰強制振動は完璧です。

次回は減衰がある場合、どうなるかについて解説しますので、楽しみにしてください。

参考文献

振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎-⑪2自由度系の非減衰強制振動の一般解

振動・波動の基礎-⑩2自由度系の非減衰強制振動と反共振点

質点\(m_1\)に外力を与えた場合

モデル

運動方程式

運動方程式の解き方

運動方程式を解く

周波数に対しての挙動

質点\(m_2\)に外力を与えた場合

モデル

運動方程式

相違点

その他の特解の取り扱いについて

まとめ

参考文献

デルタ先生の物理と数学の部屋