[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]単振動の式を習ったんだけど、これって、ずーっと振動し続けるってこと?ありえないんじゃ?[/voice]
[voice icon="https://deltapower.site/wp-content/uploads/2020/09/にっこり右側.jpg" name="デルタ先生" type="r"]うん、ありえないよ。実際には、減衰を考えないといけないんだ。[/voice]
今回は振動に関する減衰について解説します。
この減衰というものが無いと、バネだったり振り子だったりは永遠に振動し続けてしまいます。
この記事では減衰のイメージをできるだけわかりやすく解説します。
[box class="green_box" title="本記事をおススメする人"]
- 振動の減衰についてイメージがつかめていない人
- 減衰を考慮した振動の運動方程式を解きたい人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
[/box]
動画でも解説していますので、是非そちらも参考にしてください。
振動の前提条件(モデル)
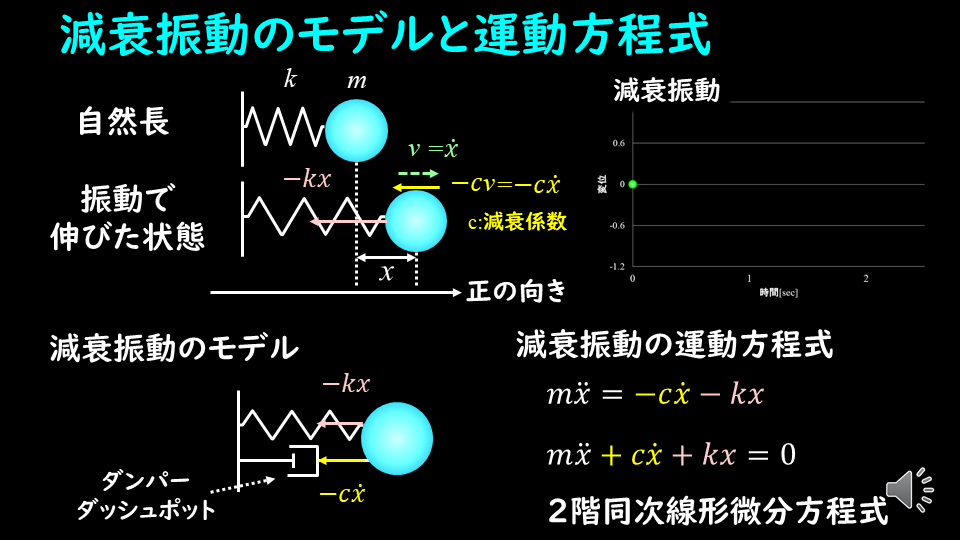
減衰のイメージというものを最初に述べます。
減衰のイメージ:振動を邪魔するもの
パラメータとしては$ζ$(ゼータ)や$c$などの減衰項で表します。
この減衰が大きいと、振動しなくなることもあります。
では、モデルの説明に入りましょう。
今回は片持ち梁の振動を例にして説明します。

片持ち梁の先端をはじいて、びよ~んと振動させると、次第に振動が収まりますよね?
これは 減衰があるために振動が徐々になくなるからです。
片持ち梁を減衰を考慮したモデルで表すと、下図のようになります。
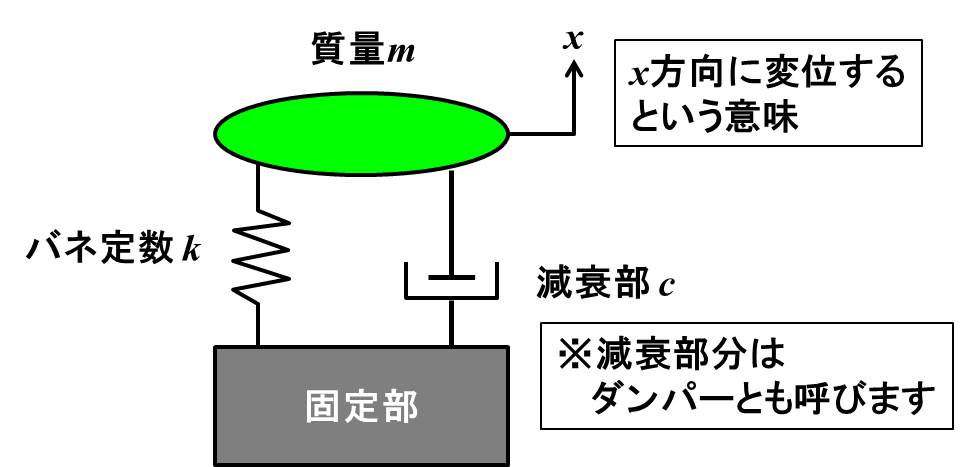
バネ定数$k$は梁の硬さと同じ意味を示します。
$c$は減衰の大きさを示す減衰係数というパラメータです。
この 減衰が物体の速度に比例して大きくなる、という前提で話を進めます。
ちなみにこのような速度に比例して大きくなる減衰を 粘性減衰と呼びます。
例としては空気抵抗とかが粘性減衰の一種ですね。
この減衰を考慮した場合の運動方程式は下記のようになります。
両辺をmで割ると
ここで、ζとωというパラメータを下のように定義します。
$$ζ = \frac{c}{2\sqrt{mk}}$$
$$ω = \sqrt{\frac{k}{m}}$$
ζは減衰比、ωは固有振動数を示します。
これらを使って運動方程式を書き換えると、下記のようになります。
この式は2階の線形微分方程式で、減衰の現象をきっちり考えるには、この方程式を解く必要があります。
この式を解いて、とある条件の解のグラフを書いてみると下記のような減衰振動のグラフが書けます。

解き方が分からない人は、結果のところまで飛ばしてください。
減衰を含んだ振動の運動方程式を解く
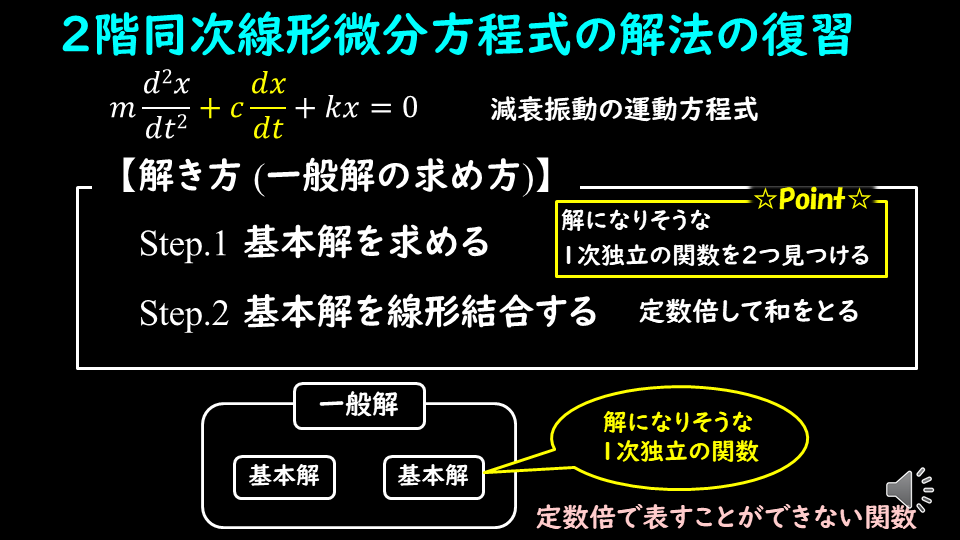
では解いていきましょう。
2階の線形微分方程式の解き方ですが、解を仮定してから、一般解を求めます。
解の仮定
まず、どのような解を仮定するか?についてです。
運動方程式をこのように変形して、左辺と右辺を見比べます。
左辺は2回、もしくは1回微分していて、右辺は微分していませんね?
左辺と右辺はイコールでつながれていますので、 解としては2回や1回の微分をしても、関数の形が変わらない式を仮定する必要があります。
微分しても変わらない関数といえば、指数関数$e^x$がありますので下記のように解を仮定します。
$$x = Ae^{λt} Aは定数$$
運動方程式に代入すると、
この式がすべての$t$に対して成立するためには
となる必要があります。
この式を特性方程式、あるいは振動数方程式といいます。
このλについての2次方程式の解は
となります。
ここで、$\sqrt{ζ^2-1}$というものがでてきて気づきましたか?
そう、 $ζ$の大きさによっては複素数になったりするので、場合分けしないといけないのです。
一般解
次に一般解です。
2階微分方程式の一般解は下記のようになります。
2階の線形微分方程式の一般解は、任意定数を含んだ2つの基本解の足し合わせ、となるのです。
2つの基本解の性質としてそれぞれが1次独立である必要があります。
$x_1 = e^{λ_1 t}$、$x_2 = e^{λ_2 t}$としますと、一般解は次のように書きかえられます。
計算が苦手な人は、上の一般解の形だけ見て、ふ~んと思って大丈夫です。
では、この一般解が、ζの値によってどうなるかについてみてみましょう。
減衰比ζによって一般解の場合分け

結論としては、下記のようになります。
[box class="pink_box" title="ζによって場合分け"]
- 過減衰:ζが1より大きい
- 臨界減衰:$ζ = 1$
- 減衰振動:ζが1より小さい
[/box]

①の過減衰が図の赤線、②の臨界減衰が図の緑線、③の減衰振動が青です。
減衰しながら振動する、という現象が起こるのはζが1より小さいとき、ということです。
振動を邪魔する減衰が大きいと振動しなくなるのはイメージしやすいと思います。
数式的にどうなっているか下記に示しますね。
$ζ>1$の場合
ζが1より大きい場合は過減衰となり、振動しません。
$$x(t) = C_1 e^{λ_1 t}+C_2 e^{λ_2 t}$$
この式の$λ_1$と$λ_2$に下記の式を入れます。
そうすると
$e^{-ωζt}$をかっこの前に出せますので、まとめると
この式から、曲線を描くと過減衰の形になります。

[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]いや、この式を見て本当に過減衰の形になるの??わかんないよ![/voice]
では別記事でもう少し詳しく計算していますので、参考にしてください。
[box class="blue_box" title="参考記事"]
[/box]
双曲線関数というものを使っていますので、そちらの解説と合わせてイメージをつかんでください。
$ζ=1$の場合
ζが1のときも振動しません。
ちょうど過減衰と減衰しながら振動するときの境目の状態です。
これは指数関数がありますので、単調に減少して$t→∞$でゼロに収束しますね。
図の緑線のようになります。

$ζ<1$の場合
ζが1より小さいとき、減衰しながら振動します。
この式の$λ_1$と$λ_2$に下記の式を入れるのですが、平方根の部分に複素数$i$を導入します。
そうすると、
$e^{-ωζt}$をかっこの前に出せますので、まとめると
この式から、勘が良い人は、三角関数が出てくることが分かると思いますが、導出します。
オイラーの公式というものがあり、下記のようになっています。
iは複素数です。オイラーの公式は非常によく使う公式ですので是非覚えておきましょう。
$ω_d = ω\sqrt{1-ζ^2}$という風において、見通し良くすると、
オイラーの公式から、
となります。
ここから実数の解を得るために、下記の計算を行います。
これらの足し合わせも一般解となりうるので、実数の一般解が下記のように書けます。
$$A,Bは定数$$
これをグラフに描くと青線のように減衰しながら振動するグラフになります。

ちなみに$ζ = 0$のときは、減衰が無い振動、すなわち単振動の時と同じ状態になります。
単振動の場合については、下記の参考記事をご覧ください。
[box class="blue_box" title="参考記事"]
[/box]
まとめ

本記事では、減衰がある場合の振動について解説しました。
減衰とは、振動を邪魔するもの、であり、減衰が大きすぎると、過減衰となり振動しなくなります。
この減衰を含んだ運動方程式を解くには2階の線形微分方程式を解く必要がありますが、
まだ習っていない高校生の方などは、結果だけをイメージとして持っていただければと思います。
減衰を考慮することで、実際の振動状態のイメージとかなり近づいたのではないでしょうか?
物理現象を理解するには、自分の頭の中でしっかりとイメージを作ることが大事です。
細かい数式を解くことも時には必要かもしれませんが、そういう時には本記事を参考にしてくださいね。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 振動・波動:小形正男、裳華房
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
