振動・波動の基礎-⑨2自由度系の非減衰自由振動具体的な振動と使い道

2自由度系では特殊解から2つのモードが出てくるってわかったけど、振幅ってどうなるの？

苦手君

デルタ先生

それじゃ、一般解からいくつかのパターンを具体的に見てみよう。

2自由度の非減衰自由振動の最終形、一般解の挙動について解説します。

前回までに、2自由度の運動方程式と、特殊解について解説していますので、運動方程式の導出について理解したい方はこちらを参考にしてください。

参考記事

本記事をおススメする人

1自由度の質点系の振動について理解したけど、多自由度系の振動について理解できていない人
2自由度の振動のイメージはついたけど、さらに深堀して理解したい人
物理を勉強していて興味がある人、仕事で振動の知識を使う人

動画でも解説していますので参考にしてください。

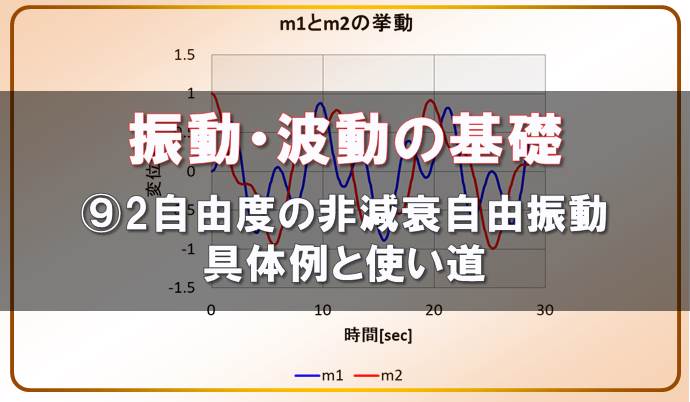
2自由度系の非減衰自由振動

モデルと運動方程式を下記に示します。

今回は非減衰の自由振動を考えますので、$c_1=c_2=0$として、下記のように書き換えます。

運動方程式は下記ですね。

$$\left(\begin{array}{cc}m_1&0\\0&m_2\end{array}\right)\left(\begin{array}{c}\ddot{x_1}\\\ddot{x_2}\end{array}\right)+\left(\begin{array}{cc}k_1+k_2&-k_2\\-k_2&k_2\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right)=0$$

見づらいので、係数を下記のように置き換えます。

$$M\ddot{X}+KX=0$$

$$M=\left(\begin{array}{cc}m_1&0\\0&m_2\end{array}\right)$$

$$K=\left(\begin{array}{cc}k_1+k_2&-k_2\\-k_2&k_2\end{array}\right)$$

$$X=\left(\begin{array}{c}x_1\\x_2\end{array}\right)$$

ここまではこの過去記事で解説しています。

これを解くと2つの振動の仕方が出てくることがわかり、下記のように2つの固有振動モードが表れます。

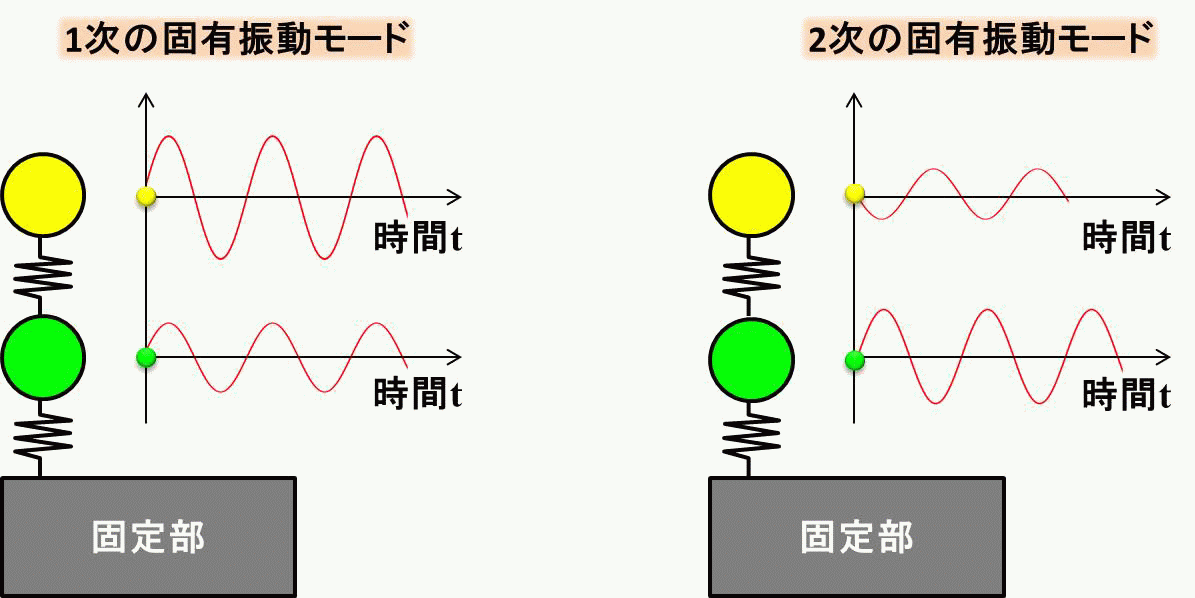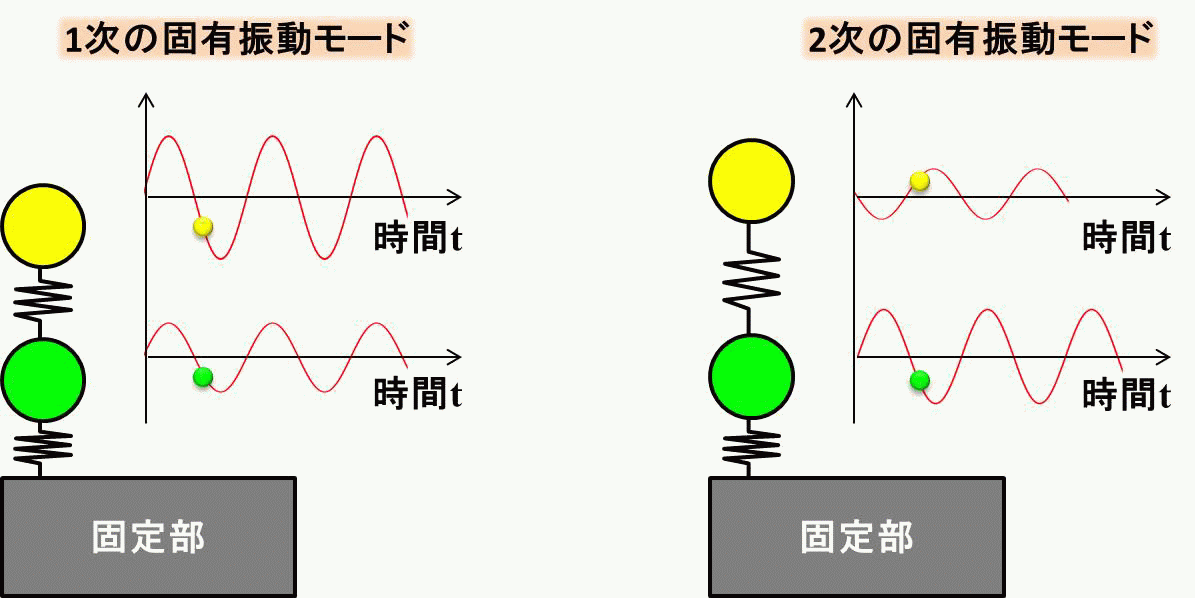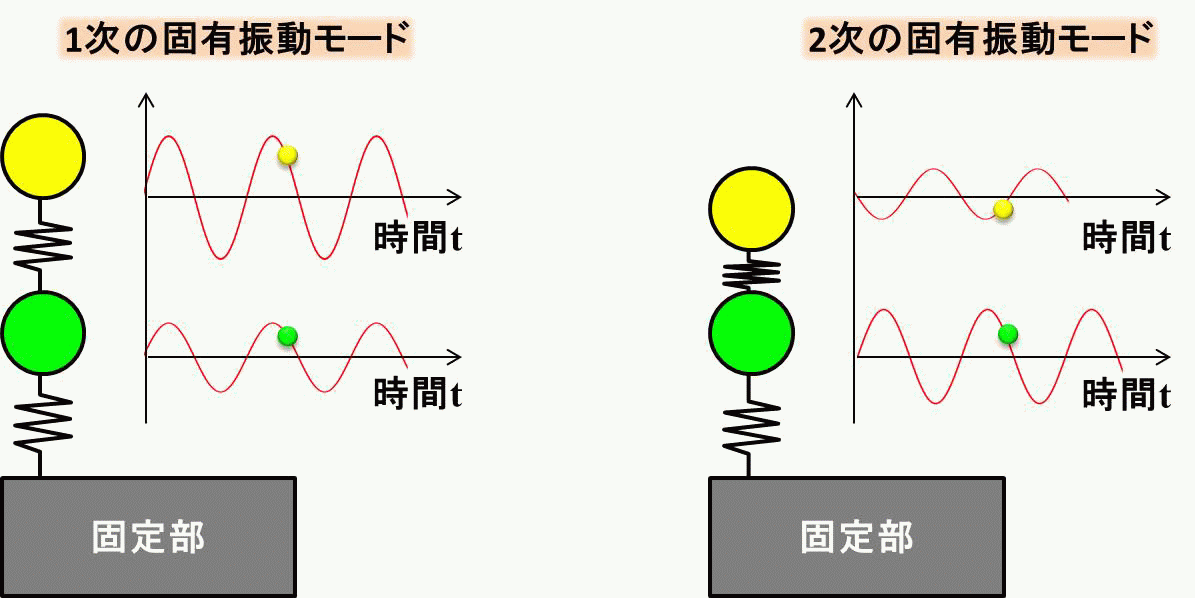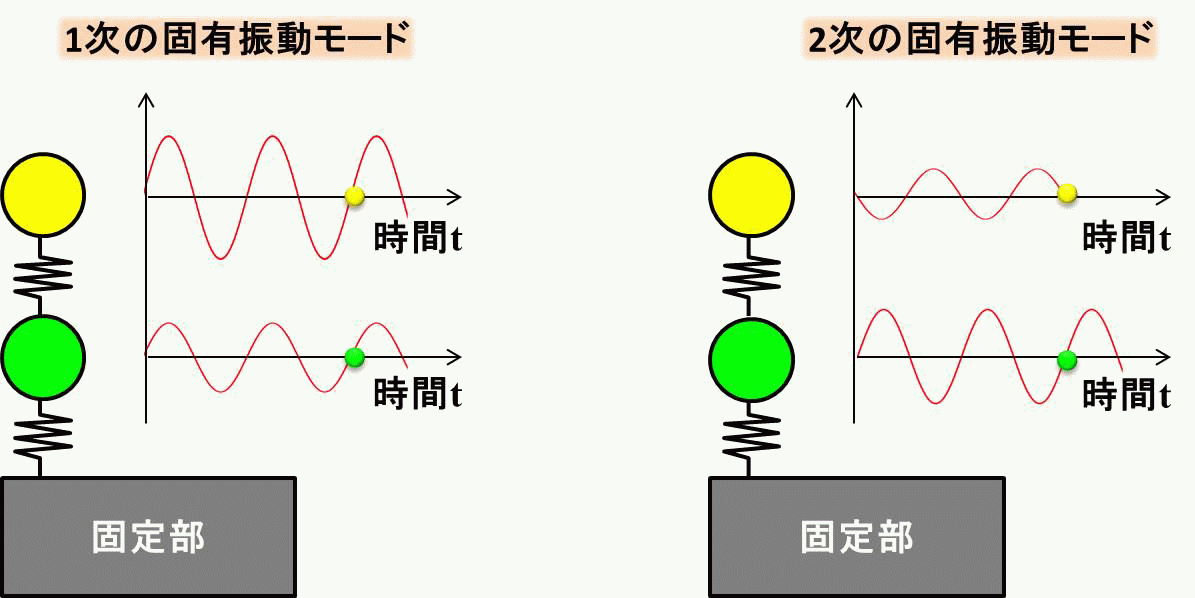
これらの振動の仕方を固有振動モード、と呼び、 左側を1次の固有振動モード、右側を2次の固有振動モードと呼びます。

それぞれの質点の振動の振幅を$u_1、u_2$と置き、$cos$型の特殊解は、

$$x_1=u_1cosωt$$

$$x_2=u_2cosωt$$

$sin$型も同じ形の特殊解になり、各モードの振幅を$u_1^1、u_2^1、u_1^2、u_2^2$とすると、

$$\left(\begin{array}{c}x_1(t)\\x_2(t)\end{array}\right)=A\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)cosω\color{red}{_1}\color{black}t+B\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)cosω\color{green}{_2}\color{black}t+C\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)sinω\color{red}{_1}\color{black}t+D\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)sinω\color{green}{_2}\color{black}t・・・①$$

ここまではこの過去記事を参考にしてください。

初期条件から振幅を計算

①式を解くわけですが、各振幅の前の係数4つが未知数になります。

A、B、C、Dですね。

ちなみに、運動方程式を解く過程で、$u_1\color{red}{^1}、u_2\color{red}{^1}$の比や、$u_1\color{green}{^2}、u_2\color{green}{^2}$の比は分かっていますので、片方が分かれば、自動的にもう片方もわかります。

未知数4つに対して、①式は2つの方程式なので、あと2つ方程式が必要です。

ということで、速度に関する式を生み出すために、変位の式を微分します。

$$\left(\begin{array}{c}\dot{x_1}(t)\\\dot{x_2}(t)\end{array}\right)=-Aω\color{red}{_1}\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)sinω\color{red}{_1}\color{black}t-Bω\color{green}{_2}\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)sinω\color{green}{_2}\color{black}t+Cω\color{red}{_1}\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)cosω\color{red}{_1}\color{black}t+Dω\color{green}{_2}\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)cosω\color{green}{_2}\color{black}t・・・②$$

ここで、初期条件$t=0$で、各質点の初期位置を$x_{10}$、$x_{20}$、各質点の初期位置を$v_{10}、v_{20}$とします。

$t=0$とすることで、①、②の$sin$の項は全て消えてくれますので、①式は

$$\left(\begin{array}{c}x_{10}\\x_{20}\end{array}\right)=A\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)+B\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)・・・③$$

②式は

$$\left(\begin{array}{c}v_{10}\\v_{20}\end{array}\right)=Cω\color{red}{_1}\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)+Dω\color{green}{_2}\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)・・・④$$

$u$に関する文字を簡単にするために、前回同様、下記のように振幅比$A_1$と$A_2$を使います。

$\color{red}{ω_1}$の時の$u_1、u_2$を$u_1\color{red}{^1}、u_2\color{red}{^1}$とし、$\frac{u_2\color{red}{^1}}{\color{black}{u_1}\color{red}{^1}}\color{black}{=}\color{red}{A_1}$、

$\color{green}{ω_2}$の時の$u_1、u_2$を$u_1\color{green}{^2}、u_2\color{green}{^2}$とし、$\frac{u_2\color{green}{^2}}{\color{black}{u_1}\color{green}{^2}}\color{black}{=}\color{green}{A_2}$とします。

$$\left(\begin{array}{c}x_{10}\\x_{20}\end{array}\right)=A'\left(\begin{array}{c}1\\A_1\end{array}\right)+B'\left(\begin{array}{c}1\\A_2\end{array}\right)・・・③'$$

$$\left(\begin{array}{c}v_{10}\\v_{20}\end{array}\right)=C'ω\color{red}{_1}\left(\begin{array}{c}1\\A_1\end{array}\right)+D'ω\color{green}{_2}\left(\begin{array}{c}1\\A_2\end{array}\right)・・・④'$$

各係数を、A'、B'、C'、D'と置いており、下記のようにしております。

$$A'=Au_1\color{red}{^1}$$

$$B'=Bu_2\color{green}{^2}$$

$$C'=Cu_1\color{red}{^1}$$

$$D'=Du_2\color{green}{^2}$$

ここまで来たら連立方程式の書き方の方がわかりやすいですね。

$$x_{10}=A'+B'・・・⑤$$

$$x_{20}=A'A_1+B'A_2・・・⑥$$

$$v_{10}=C'ω\color{red}{_1}\color{black}+D'ω\color{green}{_2}\color{black}・・・⑦$$

$$v_{20}=Cω\color{red}{_1}\color{black}A_1+Dω\color{green}{_2}\color{black}A_2・・・⑧$$

A'とB'については⑤と⑥式から、C'とD'については⑦と⑧から求まりますね。

連立方程式を解くと、下記のようになります。

$$A'=\frac{-A_2x_{10}+x_{20}}{A_1-A_2}$$

$$B'=\frac{A_1x_{10}-x_{20}}{A_1-A_2}$$

$$C'=\frac{-A_2v_{10}+v_{20}}{(A_1-A_2)ω_1}$$

$$D'=\frac{A_1v_{10}-v_{20}}{(A_1-A_2)ω_2}$$

次に振幅比$A_1$と$A_2$についての計算についてですが、これは過去の記事で詳細を計算していますので、計算過程はそちらをさんこうにしてください。

結果を記載しておくと、

$$A_1=\frac{m_1}{2k_2}\biggl\{\frac{k_1+k_2}{m_1}-\frac{k_2}{m_2}+\sqrt{(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2})^2-\frac{4k_1k_2}{m_1m_2}}\biggr\}$$

$$A_2=\frac{m_1}{2k_2}\biggl\{\frac{k_1+k_2}{m_1}-\frac{k_2}{m_2}-\sqrt{(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2})^2-\frac{4k_1k_2}{m_1m_2}}\biggr\}$$

ここまで求まりましたので、あとは具体的に初期の値を入れて、グラフを見てみましょう。

実際の2自由度系の自由振動

簡単のため、質量もバネ定数も1として計算します。。

まず、初期条件として、$x_{10}=0、x_{20}=1、v_{10}=v_{20}=0$とします。

$m_2$の質点だけ上に伸ばした状態ですね。

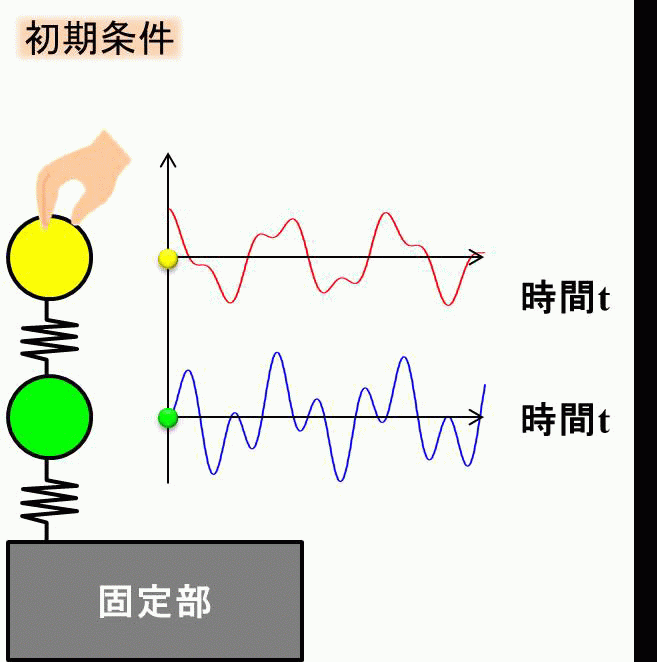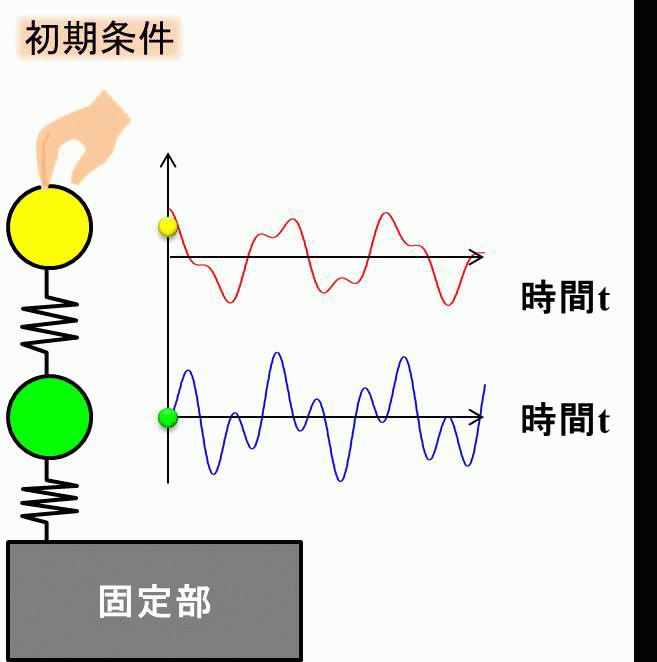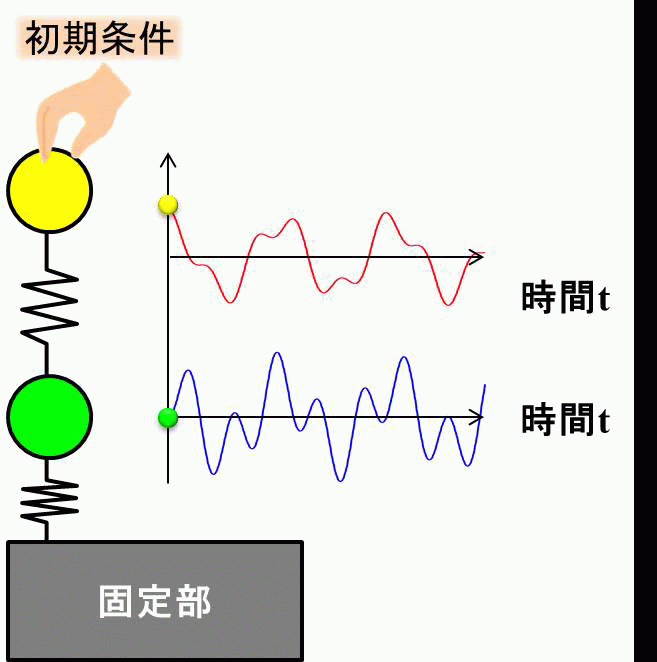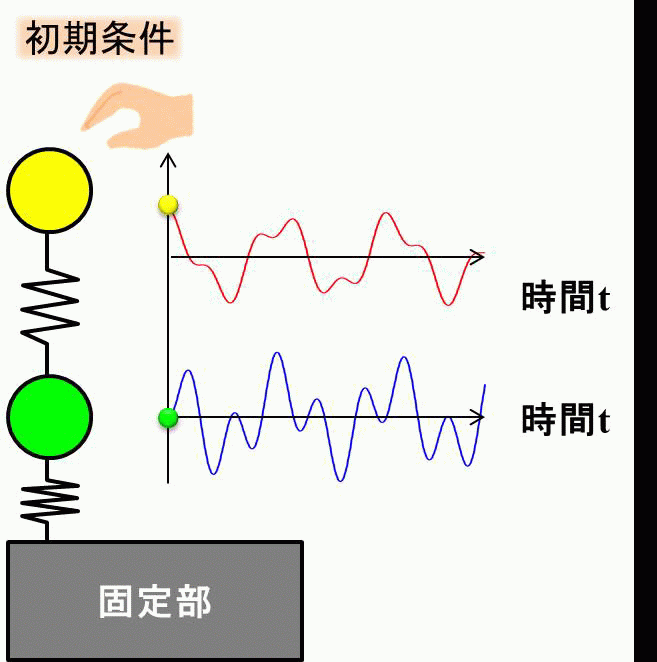
それでは、$m_1$の動きを見てみましょう。

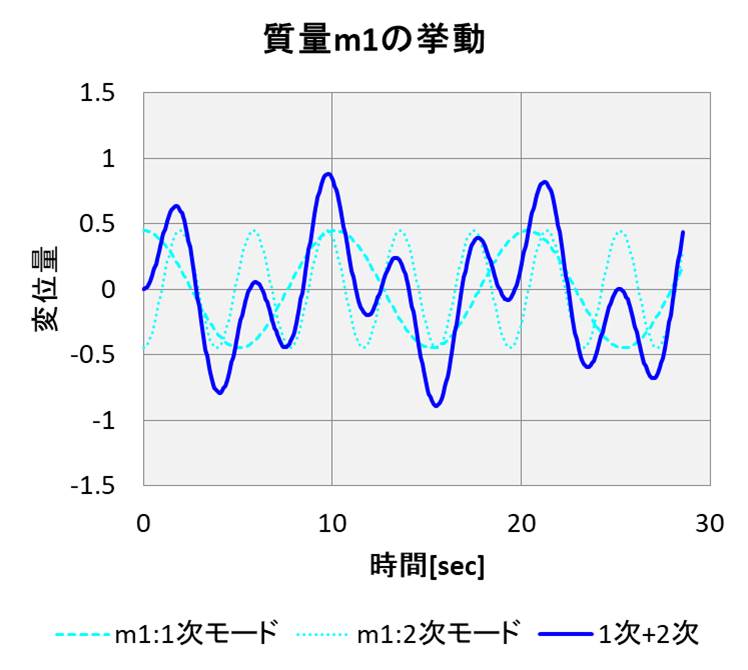
実線で挙動を示しており、2自由度系の動きは、1次モードと2次モードの足し合わせになりますので、それぞれのモードの動きを点線で示しています。

次に$m_2$の動きについても同様に見てみましょう。

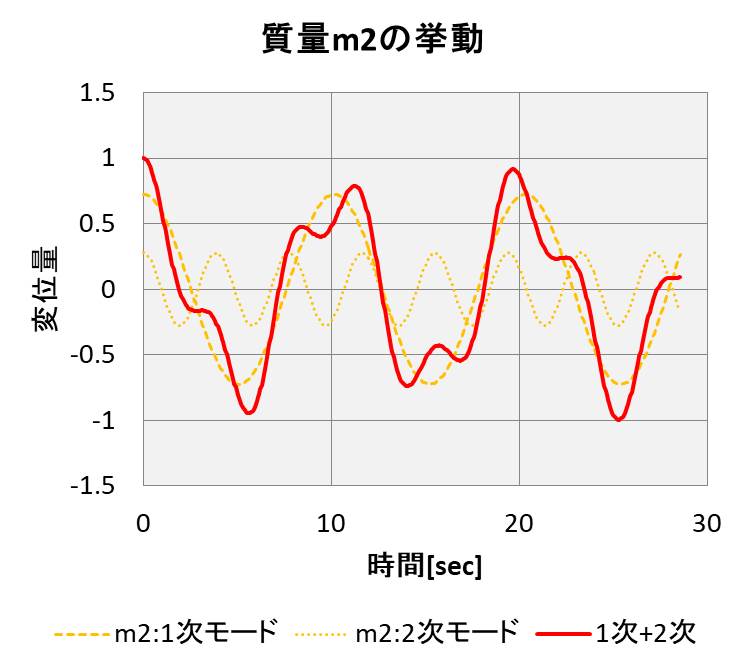
こちらも実線が実際の挙動で、点線で1次と2次のモードを示しています。

最終的には$m_1$と$m_2$は下記のようなグラフの挙動を示します。

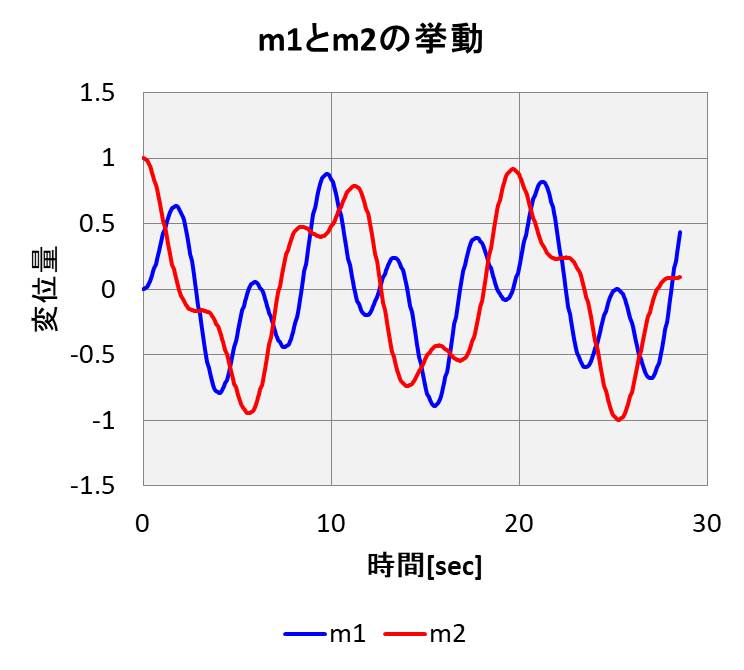
なんとも複雑な挙動ですね。

アニメーションを見ても、複雑さがイメージできると思います。

実際にこういうグラフを載せた教科書は少ないです笑。

自由振動の波形からわかること

うーん、理解できたけど、これって何かに使うの？

苦手君

デルタ先生

この波形から、固有振動モードの周波数がわかるんだ。

自由振動させると、物体は固有振動モードの周波数で振動します。

例えば、モノにガーンっと衝撃を与えて、放置すると、しばらく振動していますが、その周波数が固有振動モードの周波数で振動する、ということを意味しています。

この固有振動モードの周波数は、モノが周期的な外力と共振する周波数と一致しますので、実際のモノの共振周波数を求めるときに非常に重要になるのです。

求め方ですが、この波形をフーリエ変換することで、周波数成分の$ω_1$と$ω_2$を求めることができます。

具体的な計算は、また別途記事で説明させていただきますね。

ポイントは、 自由振動の波形をフーリエ変換することで、固有振動モードの周波数がわかる、ということです。

まとめ

本記事では、2自由度系の自由振動の計算の詳細と、実際の自由振動の使い道を説明しました。

固有振動モードが2つあるので、その重ね合わせで運動する。

その結果、複雑な振動をします。

しかし、 自由振動をフーリエ変換すると、固有振動モードの周波数がわかることがポイントでした。

振動に関わる仕事をしている人は、このことは絶対に覚えておきましょうね。

参考文献

振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎-⑩2自由度系の非減衰強制振動と反共振点

振動・波動の基礎-⑨2自由度系の非減衰自由振動 具体的な振動と使い道