振動・波動の基礎-⑧2自由度の非減衰自由振動-固有振動モード

2自由度の運動方程式はわかったけど、本当に1自由度と同じ考え方でいいの？

苦手君

デルタ先生

基本的には微分方程式を解くから同じだよ。ただ、多自由度だからこその現象もあるから、しっかり理解しようね。

本日は、2自由度の非減衰自由振動について解説します。

前回、2自由度の運動方程式について解説していますので、運動方程式の導出について理解したい方はこちらを参考にしてください。

本記事をおススメする人

1自由度の質点系の振動について理解したけど、多自由度系の振動について理解できていない人
物理を勉強していて興味がある人、仕事で振動の知識を使う人

下記動画でも解説していますので参考にしてください。

モデルと運動方程式（復習）

簡単に復習しておきます。

2自由度のモデルは下記のようになります。

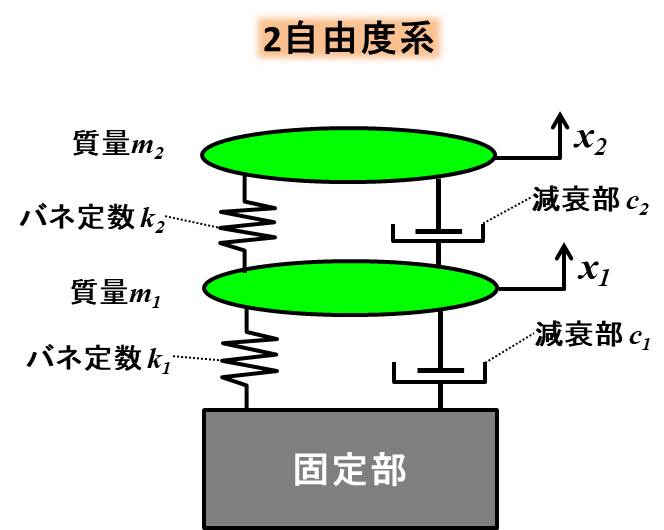
質量を$m_1、m_2$、バネ定数を$k_1、k_2$、減衰定数$c_1、c_2$と書きます。

今回は非減衰の自由振動を考えますので、$c_1=c_2=0$として、下記のように書き換えます。

運動方程式は下記ですね。

$$\left(\begin{array}{cc}m_1&0\\0&m_2\end{array}\right)\left(\begin{array}{c}\ddot{x_1}\\\ddot{x_2}\end{array}\right)+\left(\begin{array}{cc}k_1+k_2&-k_2\\-k_2&k_2\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right)=0$$

見づらいので、係数を下記のように置き換えます。

$$M\ddot{X}+KX=0$$

$$M=\left(\begin{array}{cc}m_1&0\\0&m_2\end{array}\right)$$

$$K=\left(\begin{array}{cc}k_1+k_2&-k_2\\-k_2&k_2\end{array}\right)$$

$$X=\left(\begin{array}{c}x_1\\x_2\end{array}\right)$$

いきなり行列出てきてパニックな方や、全然わけわからなくなった方はこちらの過去記事をどうぞ。

行列表記になっているだけで、基本的には1自由度系の自由振動と同じですね。

どのような振動になるか

まずは、2自由度のモデルを振動させた場合、どのような振動になるかを示しておきます。

大切なのは、 2自由度の振動には、2種類の振動の仕方がある、ということです。

具体的には下記のような振動です。

これらの振動の仕方を固有振動モード、と呼び、 左側を1次の固有振動モード、右側を2次の固有振動モードと呼びます。

さらに、左側は$m_1$も$m_2$も同じ方向に振動しているので、同位相の振動、

右側は$m_1$と$m_2$が逆方向に振動しているので、逆位相の振動と呼びます。

運動方程式を解く

アニメーションでイメージを持っていただいたところで、運動方程式を解いていきましょう。

運動方程式を解くことで、本当にこんな振動になるのかということが理解できます。

運動方程式は微分方程式を解くことですので、まずは特殊解を設定します。

2階の微分方程式の特殊解は、三角関数で置くとうまくいくことが多いので、まずは、$cos$を使ってみましょう。

$$x_1=u_1cosωt$$

$$x_2=u_2cosωt$$

ここでωは未知のパラメータとした振動周波数です。

2回微分したものは下記ですね。

$$\ddot{x_1}=-u_1ω^2cosωt$$

$$\ddot{x_2}=-u_2ω^2cosωt$$

これらを下記の運動方程式に代入しましょう。

$$m_1\ddot{x_1}+(k_1+k_2)x_1-c_2\dot{x_2}-k_2x_2=0・・・①$$

$$m_2\ddot{x_2}+k_2x_2-k_2x_1=0・・・②$$

①式は

$$m_1(-ω^2u_1cosωt)+(k_1+k_2)u_1cosωt-k_2u_2cosωt=0$$

②式は

$$m_2(-ω^2u_2cosωt)-k_2u_1cosωt+k_2u_2cosωt=0$$

これらは$cosωt$を消去できるので、消去して、$u_1$と$u_2$で整理すると、

$$(-ω^2m_1+k_1+k_2)u_1-k_2u_2=0・・・③$$

$$-k_2u_1+(-ω^2m_2+k_2)u_2=0・・・④$$

これらを行列表記すると、

$$\left(\begin{array}{cc}-ω^2m_1+k_1+k_2&-k_2\\-k_2&-ω^2m_2+k_2\end{array}\right)\left(\begin{array}{c}u_1\\u_2\end{array}\right)=0$$

この式を満たすωを考えるのですが、ここで少し線形代数学の知識をつかいます。

$u_1、u_2$の組み合わせとして、$u_1=u_2=0$の場合、ωは何でもよくなってしまいますので、 $u_1$も$u_2$もゼロでないことを条件とします。

このことを線形代数学では、$u_1$と$u_2$は1次従属の関係にあると言います。

1次従属の場合、 $u_1$と$u_2$は比しか求まりません。

③から$\frac{u_2}{u_1}$の式に直すと、

$$\frac{u_2}{u_1}=\frac{-ω^2m_1+k_1+k_2}{k_2}・・・⑤$$

1次従属となるような連立方程式（行列）の係数の条件は、 $det=0$で求まりますね。

$$det\left[\begin{array}{cc}-ω^2m_1+k_1+k_2&-k_2\\-k_2&-ω^2m_2+k_2\end{array}\right]=0$$

行列式の計算なので、下記のようになります。

$$(-ω^2m_1+k_1+k_2)(-ω^2m_2+k_2)-k_2^2=0$$

これをωの式に変形すると、

$$m_1m_2ω^4-\{(k_1+k_2)m_2+k_2m_1\}ω^2+k_1k_2=0$$

$ω^2$の2次方程式とみなすことができ、これを 振動数方程式（特性方程式）と呼びます。

2次方程式の解の公式から、

$$ω^2=\frac{1}{2}\biggl\{\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2}±\sqrt{(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2})^2-\frac{4k_1k_2}{m_1m_2}}\biggr\}$$

ωは正の値なので、$ω>0$となる解は

$$ω=\sqrt{\frac{1}{2}\biggl\{\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2}±\sqrt{(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2})^2-\frac{4k_1k_2}{m_1m_2}}}\biggr\}$$

ルートの中に±が存在するので、解が2つあることになります。

解を$ω_1、ω_2$とおき、$ω_1<ω_2$とすると、$ω_1$が1次の固有振動モード、$ω_2$が2次の固有振動モードと呼びます。

$\color{red}{ω_1}$の時の$u_1、u_2$を$u_1\color{red}{^1}$、$u_2\color{red}{^1}$とし、$\frac{u_2\color{red}{^1}}{\color{black}{u_1}\color{red}{^1}}\color{black}{=}\color{red}{A_1}$、

$\color{green}{ω_2}$の時の$u_1、u_2$$u_1\color{green}{^2}$、$u_2\color{green}{^2}$とし、$\frac{u_2\color{green}{^2}}{\color{black}{u_1}\color{green}{^2}}\color{black}{=}\color{green}{A_2}$とします。

さらに、$ω_1、ω_2$を⑤の式に代入して、各モードの振幅比Aを求めます。

$$A_1=-\frac{m_1}{k_2}・\frac{1}{2}\biggl\{\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2}-\sqrt{(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2})^2-\frac{4k_1k_2}{m_1m_2}}\biggr\}+\frac{k_1+k_2}{k_2}$$

整理すると、

$$A_1=\frac{m_1}{2k_2}\biggl\{\frac{k_1+k_2}{m_1}-\frac{k_2}{m_2}+\sqrt{(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2})^2-\frac{4k_1k_2}{m_1m_2}}\biggr\}$$

同様に、$A_2$を求めます。ルートの前の符号が異なるだけですから、

$$A_2=\frac{m_1}{2k_2}\biggl\{\frac{k_1+k_2}{m_1}-\frac{k_2}{m_2}-\sqrt{(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2})^2-\frac{4k_1k_2}{m_1m_2}}\biggr\}$$

と計算できます。

ここで、$A_1$と$A_2$のルートの前の部分とルートの中身の大小関係を見てみましょう。

ルートの中身は

$$(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2})^2-\frac{4k_1k_2}{m_1m_2}=(\frac{k_1+k_2}{m_1})^2+(\frac{k_2}{m_2})^2+2(\frac{k_1+k_2}{m_1m_2})k_2-\frac{4k_1k_2}{m_1m_2}・・・⑥$$

これとルートの前の部分との大小関係を見たいので、ルートの前の部分を2乗します。

$$(\frac{k_1+k_2}{m_1}-\frac{k_2}{m_2})^2=(\frac{k_1+k_2}{m_1})^2+(\frac{k_2}{m_2})^2-\frac{2k_1k_2}{m_1m2}・・・⑦$$

⑦+⑥が1次の固有振動モードなので、計算してみると、

$$2((\frac{k_1+k_2}{m_1})^2+(\frac{k_2}{m_2})^2-\frac{2k_1k_2}{m_1m_2})=2(\frac{k_1}{m_1}-\frac{k_2}{m_2})^2+\frac{2k_1k_2}{m_1}+(\frac{k_2}{m_1})^2>0$$

⑦-⑥は2次の固有振動モードなので、こちらも計算すると

$$-2\frac{k_1k_2}{m_1m2}-2(\frac{k_1+k_2}{m_1m_2})k_2+\frac{4k_1k_2}{m_1m_2}=-\frac{2k_2^2}{m_1m_2}<0$$

となり、1次の場合、振幅の比は$A_1>0$、2次の場合、振幅の比は$A_2<0$となります。

つまり、1次の時は、同じ方向に振幅するが、2次の場合、逆方向に振動する、ということです。

これを示したのが、冒頭のアニメーションになります。

さて、一般解の形まで導出しましょう。

特殊解を、1次の場合$x_1\color{red}{^1}$、$x_2\color{red}{^1}$、2次の場合$x_1\color{green}{^2}、x_2\color{green}{^2}$、と書き直します。

そうすると、

$$\left(\begin{array}{c}x_1\color{red}{^1}\\x_2\color{red}{^1}\end{array}\right)=\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)cosω\color{red}{_1}\color{black}t$$

$$\left(\begin{array}{c}x_1\color{green}{^2}\\x_2\color{green}{^2}\end{array}\right)=\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)cosω\color{green}{_2}\color{black}t$$

以上で、$cos$と置いた時の特殊解が求まりました。

$cos$でもOKなのであれば・・・そう、$sin$でも同じです。

2回微分した形も$sin$に置き換わるだけですし、連立方程式のところで$sin$は消去しますので、 特殊解の形は同じになります。

よって、$sin$と置いた時の特殊解は、

$$\left(\begin{array}{c}x_1\color{red}{^1}\\x_2\color{red}{^1}\end{array}\right)=\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)sinω\color{red}{_1}\color{black}t$$

このようになります。

一般解はこれらの線形結合で表されますので、

$$\left(\begin{array}{c}x_1(t)\\x_2(t)\end{array}\right)=A\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)cosω\color{red}{_1}\color{black}t+B\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)cosω\color{green}{_2}\color{black}t+C\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)sinω\color{red}{_1}\color{black}t+D\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)sinω\color{green}{_2}\color{black}t$$

あとは、初期条件が与えられたときに、未知数を求めればよいです。

係数を別の記事で求めますので、参考にしてください。

まとめ

2自由度の非減衰自由振動の固有振動モードについて解説しました。

行列を取り扱うので、苦手な人は計算が、難しいかもしれませんが、下記を抑えましょう。

ポイント

2自由度の振動では、運動方程式の解き方は1自由度と同じ微分方程式を解く
多自由度の振動では固有振動モードが存在
2自由度の振動では同位相と逆位相の2つの固有振動モードがある

あとは、アニメーションをじっくり見て、こういう2つの振動モードがある、というイメージをもちましょう。

複数の振動モードがある、という認識ができれば、質点が増えても応用がきいてきますので、覚えておいてくださいね。

記事内容で理解できない方は下記の動画でも解説していますので参考にしてください。

参考文献

振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎-⑨2自由度系の非減衰自由振動具体的な振動と使い道