振動・波動の基礎-⑦2自由度系の運動方程式行列表現を使って見やすくしよう

[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]これまでは1つの質点の振動だったけど、2つとか出てきて意味わかんなくなってきたよ…[/voice]

[voice icon="https://deltapower.site/wp-content/uploads/2020/09/にっこり右側.jpg" name="デルタ先生" type="r"]多自由度系の振動についてだね。行列とかが出てくるから、計算が面倒になるけど、考え方は大きく変わらないよ。[/voice]

本記事から多自由度系の振動について解説します。

これまでは1つの質点についての振動を考えましたが、実際の物体は質点ではないですよね？

多自由度系で考えることで、より現実に近い、リアルな表現ができます。

今回は、多自由度系で一番簡単な2自由度系について解説します。

質点の振動について最初から知りたい方は下記の記事を参考にしてください。

[box class="blue_box" title="参考記事"]

振動・波動の基礎①-古典的な調和振動子（単振動）

[/box]

[box class="green_box" title="本記事をおススメする人"]

1自由度の質点系の振動について理解したけど、多自由度系について理解できていない人
物理を勉強していて興味がある人、仕事で振動の知識を使う人

[/box]

2自由度系とは

まずはこれまでの1自由度の時との比較として、どのようなものを2自由度系と呼ぶのかを見てみましょう。

モデル

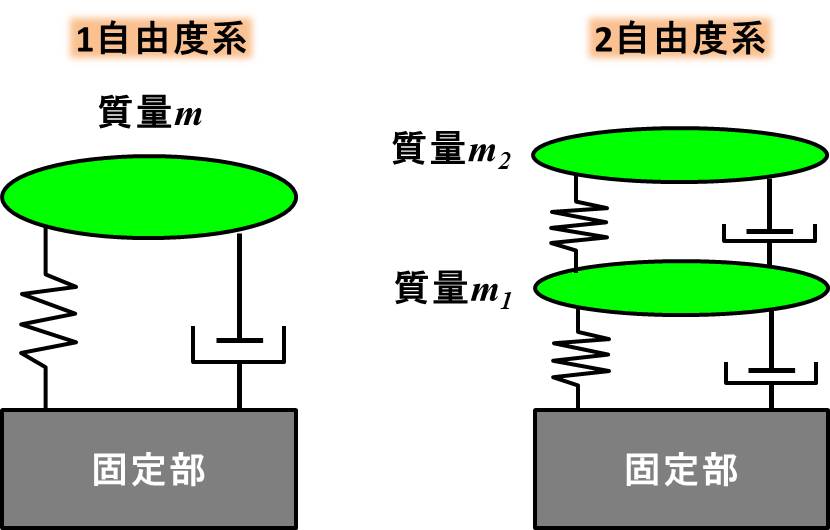
左側がこれまでの1自由度のモデル、右側が2自由度のモデルです。

錘が2つ、バネが2つ、減衰のダンパーが2つ、ということですべてが2つになっています。

ではこのときの運動方程式を考えてみましょう。

運動方程式

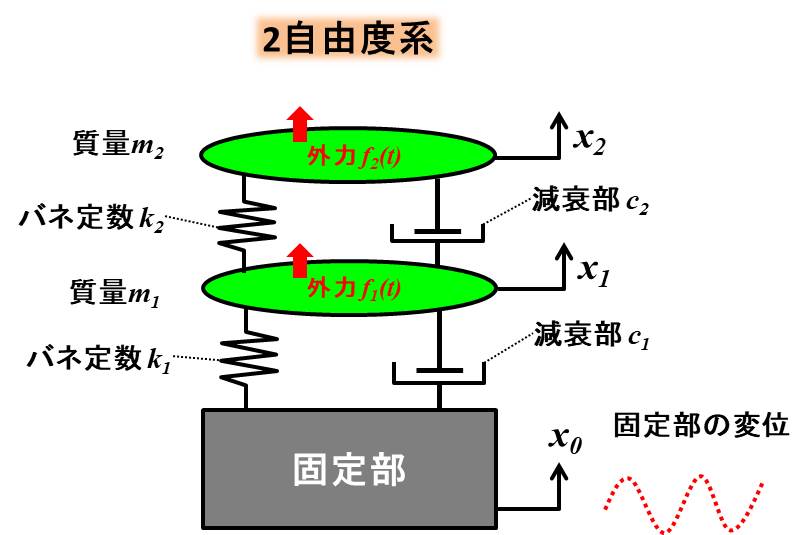
上記の２自由度系のモデルのパラメータを設定しましょう。

2つの質量を$m_1$、$m_2$、バネ定数を$k_1$、$k_2$、減衰定数を$c_1$、$c_2$とします。

つながっている土台が動くような振動、つまり変位振動を考えると、固定部の変位を$x_0$、$m_1$、$m_2$の質量の錘の変位をそれぞれ$x_1$、$x_2$とします。

最後に$m_1$、$m_2$の質量の錘に与える外力をそれぞれ$f_1(t)$、$f_2(t)$と置きます。

いろいろ設定しましたが、まとめると下図のような感じです。

さて、運動方程式を考えるのですが、動くものが$m_1$、$m_2$と2つあるので、運動方程式は2つ用意できます。

$m_1$についての運動方程式を考えるために、どのような力が$m_1$に働いているか整理しましょう。

働いている力をまとめると、下記の5つです。

バネ$k_1$からの力：$\color{red}{-k_1(x_1-x_0)}$
バネ$k_2$からの力：$\color{blue}{-k_2(x_1-x_2)}$
減衰力$c_1$の力：$\color{green}{-c_1(\dot{x_1}-\dot{x_0})}$
減衰力$c_2$の力：$\color{magenta}{-c_2(\dot{x_1}-\dot{x_2})}$
外力：$f_1(t)$

運動方程式は以上の力が右辺に書かれるので、色分けして書くと、下記のようになります。

$$m_1\ddot{x_1}=\color{red}{-k_1(x_1-x_0)}\color{blue}{-k_2(x_1-x_2)}\color{green}{-c_1(\dot{x_1}-\dot{x_0})}\color{magenta}{-c_2(\dot{x_1}-\dot{x_2})}\color{black}{+f_1(t)}$$

もう少しこれまでの数式の形に近づけたいので、未知のパラメータと既知のパラメータで分けましょう。

既知のパラメータとは、問題設定や事前に測定するなどで、解く前から値が与えられるパラメータ 、ということです。

この式の未知のパラメータは$x_1$と$x_2$、さらにはその微分形の$\dot{x_1}$、$\dot{x_2}$、$\ddot{x_1}$で、他のパラメータは全て既知の値です。

未知のパラメータを左辺に、既知のパラメータを右辺に持っていくように整理します。

$$m_1\ddot{x_1}+(c_1+c_2)\dot{x_1}+(k_1+k_2)x_1-c_2\dot{x_2}-k_2x_2=c_1\dot{x_0}+k_1x_0+f_1(t)・・・①$$

次に$m_2$についての運動方程式を考えましょう。

$m_2$に働いている力をまとめると、こちらは下記の3つです。

バネ$k_2$からの力：$\color{blue}{-k_2(x_2-x_1)}$
減衰力$c_2$の力：$\color{magenta}{-c_2(\dot{x_2}-\dot{x_1})}$
外力：$f_2(t)$

運動方程式は下記のようになります。

$$m_2\ddot{x_2}=\color{blue}{-k_2(x_2-x_1)}\color{magenta}{-c_2(\dot{x_2}-\dot{x_1})}\color{black}={f_2(t)}$$

これも$m_1$の時と同じように、左辺に未知のパラメータ、右辺に既知のパラメータと式変形します。

$$m_2\ddot{x_2}+c_2\dot{x_2}+k_2x_2-c_2\dot{x_1}-k_2x_1=f_2(t)・・・②$$

これがそれぞれの運動方程式の形になります。

連成項

①と②式を並べてみましょう。

$$m_1\ddot{x_1}+(c_1+c_2)\dot{x_1}+(k_1+k_2)x_1\color{red}{-c_2\dot{x_2}-k_2x_2}\color{black}=c_1\dot{x_0}+k_1x_0+f_1(t)・・・①$$

$$m_2\ddot{x_2}+c_2\dot{x_2}+k_2x_2\color{red}{-c_2\dot{x_1}-k_2x_1}\color{black}=f_2(t)・・・②$$

赤字で示す部分ですが、①式には$x_2$による項が、②式には$x_1$による項が入っていますね？

これらは他の質点からの交互作用を示す項として、連成項(Coupling Term）と呼ばれています。

連成項があるからイメージがつきにくかったり、方程式も解くのが面倒だったりします。

しかし、このような連成項をうま～く記述できる方法があります。

それが 行列表記なんですね。

多自由度系では行列を避けて通ることはできませんので、この行列表記に慣れていきましょう。

行列表記に変換

[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]ヤダヤダ！行列キライ！！[/voice]

[voice icon="https://deltapower.site/wp-content/uploads/2020/09/にっこり右側.jpg" name="デルタ先生" type="r"]じっくり読んでいけば理解できるので、時間をかけてでもここは理解していこうね。[/voice]

もう一度、①式と②式を並べましょう。

$$m_1\ddot{x_1}+(c_1+c_2)\dot{x_1}+(k_1+k_2)x_1\color{red}{-c_2\dot{x_2}-k_2x_2}\color{black}=c_1\dot{x_0}+k_1x_0+f_1(t)・・・①$$

$$m_2\ddot{x_2}+c_2\dot{x_2}+k_2x_2\color{red}{-c_2\dot{x_1}-k_2x_1}\color{black}=f_2(t)・・・②$$

これらを行列表記します。

$$\left(\begin{array}{cc}m_1&0\\0&m_2\end{array}\right)\left(\begin{array}{c}\ddot{x_1}\\\ddot{x_2}\end{array}\right)+\left(\begin{array}{cc}c_1+c_2&-c_2\\-c_2&c_2\end{array}\right)\left(\begin{array}{c}\dot{x_1}\\\dot{x_2}\end{array}\right)+\left(\begin{array}{cc}k_1+k_2&-k_2\\-k_2&k_2\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right)=\left(\begin{array}{c}k1x_0+c_1\dot{x_0}+f_1(t)\\f_2(t)\end{array}\right)$$

質量マトリックスをM、減衰マトリックスをC、剛性マトリックスをK、外力ベクトルをF、位置を表すベクトルをXとして、下記のように置きます。

$$M=\left(\begin{array}{cc}m_1&0\\0&m_2\end{array}\right)$$

$$C=\left(\begin{array}{cc}c_1+c_2&-c_2\\-c_2&c_2\end{array}\right)$$

$$K=\left(\begin{array}{cc}k_1+k_2&-k_2\\-k_2&k_2\end{array}\right)$$

$$F=\left(\begin{array}{c}k1x_0+c_1\dot{x_0}+f_1(t)\\f_2(t)\end{array}\right)$$

$$X=\left(\begin{array}{c}x_1\\x_2\end{array}\right)$$

これらのように置くと、運動方程式は

$$M\ddot{X}+C\dot{X}+KX=F$$

このように、1自由度系の運動方程式に非常に近い形で表すことができます。

ただし、これらは行列表記になっていることに注意しましょう。

係数となる行列の性質

MとかCとかKとかいろいろマトリックスが出てきましたが、これらは 対称行列になっています。

例えば剛性マトリックスKの非対角項ですが、ともに$-k_2$となっていますね？

下記のように剛性マトリックスを書くと、

$$K=\left(\begin{array}{cc}k_{11}&k_{12}\\k_{21}&k_{22}\end{array}\right)$$

$k_{12}$は質量$m_1$が$x_2$の変位によって受ける力なので、①式から$-k_2$、

$k_{21}$は質量$m_2$が$x_1$の変位によって受ける力なので、②式から$-k_2$となって、一致します。

Cなどのマトリックスも同様なので、対称行列になります。

まとめ

本記事では2自由度系の運動方程式について解説しました。

2自由度系の運動方程式は行列で表現すると、1自由度で表現できます。

またそれぞれの係数のマトリックスは対称行列になっています。

このことさえ理解できれば、あとは1自由度系と考え方はほとんど同じです。

ちょっと行列の計算が面倒だったりしますが、まずは現象を理解して、イメージをつけましょう。

参考文献

振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

本サイトの振動工学のページはこちら。

振動・波動の基礎-⑦2自由度系の運動方程式 行列表現を使って見やすくしよう