1次元の強制振動における共振の計算減衰がある場合の挙動について

強制振動における共振の計算について詳細を示します。

本記事では減衰項ありで計算します。

本記事をおススメする人

減衰が入った共振の運動方程式が解けない人
仕事で構造物の設計をする人、大学で振動の研究をしはじめた人

強制振動の共振と、減衰が無い場合については下記の過去記事を参考にしてください。

参考記事

振動・波動の基礎　③強制振動と共振について

強制振動における共振の計算（減衰無し）

減衰が無い場合と同じく、微分方程式を解く必要があります。

式も少し複雑ですが、できるだけ簡潔にわかりやすく解説します。

動画での解説もありますので、下記動画も参考にしてください。

動画では周期的外力を$sin$として計算しています。

減衰のある振動の運動方程式を解く

減衰のある自由振動の運動方程式

強制振動の話をする前に、質量に周期的な外力が無い場合を考えます。

詳細は下記の記事で解説していますので、まず外力が無い場合を理解してから読んでください。

参考記事

振動・波動の基礎②-振動の減衰

減衰振動の計算-過減衰の形と双曲線関数

減衰のある振動は、下記のようなモデルで表すことができます。

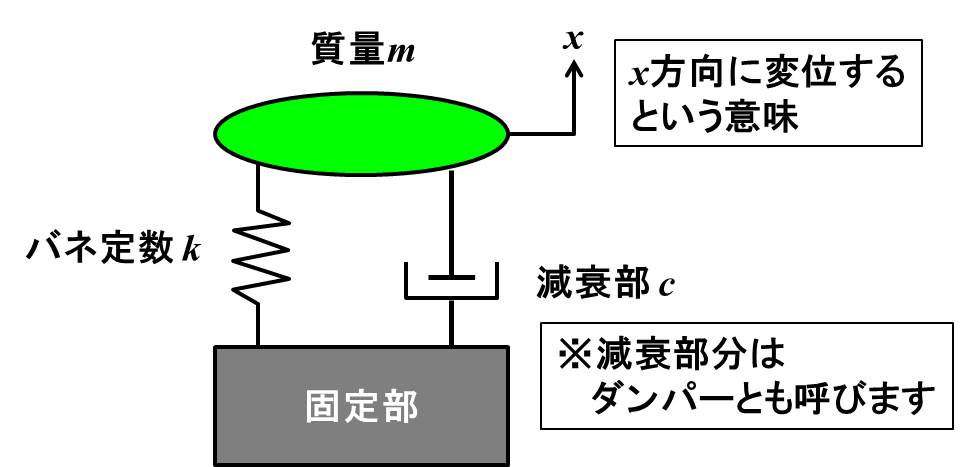
減衰は速度に比例する粘性減衰を仮定しています。

この運動方程式は下記のようになります。

$$m\ddot{x}+c\dot{x}+kx = 0$$

これが『減衰のある自由振動の運動方程式』です。

減衰のある強制振動の運動方程式

では、強制的に振動するように、質量の部分に周期的な外力を付け加えてみましょう。

角振動数$ω$で周期的に変化する外力を、$Fcosωt$としますと、

$$m\ddot{x}+c\dot{x}+kx = Fcosωt$$

となります。右辺に$Fcosωt$がくっつきました。

整理するために、両辺を$m$で割ると

$$\ddot{x}+\frac{c}{m}\dot{x}+\frac{k}{m}x = \frac{F}{m}cosωt$$

ここで、$ζ、ω_0、f$の3つのパラメータを下のように定義します。

$$ζ = \frac{c}{2\sqrt{mk}}$$

$$ω_0 = \sqrt{\frac{k}{m}}$$

$$f =\frac{F}{m}$$

ζは減衰比、$ω_0$は固有振動数を示します。

これらを使って運動方程式を書き換えると、下記のようになります。

$$\ddot{x}+2ζω_0\dot{x}+ω^2_0x - fcosωt =0$$

教科書とかでもよく出てくる形ですね。

$ζω_0 = γ$としている参考書などもありますが、本質的には同じです。

微分方程式を解く

ここから運動方程式を解いて、一般解を求めていきます。

$$\ddot{x}+2ζω_0\dot{x}+ω_0^2x - fcosωt =0$$

解き方ですが、この微分方程式の解は

同次方程式の一般解 + 非同次微分方程式の特殊解

となります。同次方程式の一般解というのは、外力が無い場合の一般解です。

同次方程式の一般解

下記の記事で詳細を計算していますので、結果だけお見せします。

参考記事

振動・波動の基礎②-振動の減衰

減衰振動の計算-過減衰の形と双曲線関数

一般解は、下記です。

$$x(t) = C_1 e^{λ_1 t}+C_2 e^{λ_2 t}$$

$$λ = -ζω±ω\sqrt{ζ^2-1}$$

減衰比ζの値で場合分けしてグラフを書きます。

ζが1より小さいときにはじめて振動します。

ここで大事なのは、 ζの値に関わらず、この一般解はt→∞で0に収束する、ということです。

同次方程式の一般解としては上記を理解しておけば大丈夫です。

特殊解を求める

それでは特殊解を仮定します。

$x=Acosωt + Bsinωt$と特解を仮定すると、微分したものは下記のようになります。

$$\ddot{x} = -Aω^2cosωt -Bω^2sinωt$$

$$\dot{x} = -Aωsinωt +Bωcosωt$$

これらを運動方程式に代入します。

$$-Aω^2cosωt-Bω^2sinωt+2ζω_0(-Aωsinωt +Bωcosωt)+ω_0^2(Acosωt + Bsinωt)-fcosωt=0$$

見通し良くするためにcosとsinの項で分けます。

$$cosωt(-Aω^2+2Bζω_0ω+Aω_0^2-f)$$

$$+sinωt(-Bω^2-2Aζω_0ω+Bω_0^2)=0$$

ここで、$cos、sin$の係数がそれぞれゼロになるようにして、$A$と$B$を求めます。

$$-Aω^2+2Bζω_0ω+Aω_0^2-f=0$$

$$-Bω^2-2Aζω_0ω+Bω_0^2=0$$

となります。$A$と$B$を求めたいので、これらの式を$A$と$B$で整理すると

$$A(ω_0^2-ω^2)+2Bζω_0ω=f・・・①$$

$$-2Aζω_0ω+B(ω_0^2-ω^2)=0・・・②$$

この連立方程式を解けばよいので、解きましょう、つべこべ言わずに笑

$B$を消去するために$B$の係数で①式、②式の両辺をそれぞれ割ります。

$$A\frac{(ω_0^2-ω^2)}{2ζω_0ω}+B=\frac{f}{2ζω_0ω}・・・①'$$

$$\frac{-2Aζω_0ω}{(ω_0^2-ω^2)}+B=0・・・②'$$

①'-②'より

$$A{\frac{(ω_0^2-ω^2)}{2ζω_0ω}+\frac{2ζω_0ω}{(ω_0^2-ω^2)}}=\frac{f}{2ζω_0ω}$$

左辺を通分して、

$$A{\frac{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}{2ζω_0ω(ω_0^2-ω^2)}}=\frac{f}{2ζω_0ω}$$

$A$の係数で両辺を割って$A$を求めると

$$A=\frac{f(ω_0^2-ω^2)}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}$$

この$A$を今度は②'式に入れて、$B$を求めます。

$$B = A\frac{2ζω_0ω}{ω_0^2-ω^2} =\frac{f(ω_0^2-ω^2)}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}・\frac{2ζω_0ω}{ω_0^2-ω^2}$$

整理すると

$$B=\frac{2fζω_0ω}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}$$

これで$A$と$B$が求まりました。

$x=Acosωt + Bsinωt$と特解を仮定していましたので、ここに代入します。

$$x = \frac{f(ω_0^2-ω^2)}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}cosωt+\frac{2fζω_0ω}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}sinωt$$

分母と分子の$f$が$cos$と$sin$の項で共通なので、かっこでくくります。

$$x=\frac{f}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}\{(ω_0^2-ω^2)cosωt+2ζω_0ωsinωt\}$$

さて、ここからさらに変形するのですが、三角関数の以下の公式は覚えていますか？

三角関数の合成公式

$$Csinx+Dcosx = \sqrt{C^2+D^2}sin(x-δ)$$

$$tanδ = \frac{C}{D}$$

この公式を使います。

$$x=\frac{f}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}sin(ωt-δ)$$

$$tanδ =\frac{2ζω_0ω}{ω_0^2-ω^2}$$

$x$の式を整理しますと、

$$x=\frac{f}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}sin(ωt-δ)$$

このようになります。三角関数が$sin$一つだけになりましたね。

これで特解が求まりました。

一般解から振動の様子を見る

$$\ddot{x}+2ζω_0\dot{x}+ω_0^2x - fcosωt =0$$

この微分方程式の解は

同次方程式の一般解 + 非同次方程式の特解

となります。下記に同次方程式の一般解を示します。

$$x(t) = C_1 e^{λ_1 t}+C_2 e^{λ_2 t}・・・③$$

$$λ = -ζω±ω\sqrt{ζ^2-1}$$

特解は先ほど求めましたね。

$$x(t)=\frac{f}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}sin(ωt-δ)・・・④$$

$$tanδ = \frac{2ζω_0ω}{ω_0^2-ω^2}$$

③と④を足し合わせたものが解になりますね。

$$x(t) = C_1 e^{λ_1 t}+C_2 e^{λ_2 t}+\frac{f}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}sin(ωt-δ)・・・⑤$$

というわけで一般解が求まりました。

ここから振動の様子を見ていきます。

$t→∞$としたとき、⑤はどうなるか？についてです。

最初の2項の指数関数の部分は、外力が無い場合の減衰振動を示していますので、$t→∞$とすると、0に収束します。

つまり、 十分な時間が経つと特解の部分だけが残り、sinの項で振動するわけですね。

$sin$の係数が振幅になりますので、振幅を$X$と置きますと、

$$X=\frac{f}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}・・・⑥$$

この振幅が角振動数ωによってどのように変化するかを見ていきます。

上式の分母が最小値になるωがピークの値になりますので、このときのωを求めます。

分母のルートの中身だけ取り出して整理しましょう。$ω_0^4$でくくります。

$$(ω_0^2-ω^2)^2+(2ζω_0ω)^2=ω_0^4\{(1-\frac{ω^2}{ω_0^2})^2+4ζ^2\frac{ω^2}{ω^2_0}\}$$

最小値となるωを議論したいので、係数の$ω_0^4$は無視できます。

さらに$\frac{ω^2}{ω_0^2} = Ω$と置きますと、

$$(1-Ω^2)^2+4ζ^2Ω^2 = Ω^2-2(1-2ζ^2)Ω+1$$

と整理できますので、Ωの２次方程式の最小値を求める問題になります。

このときの最小値を求めるために式変形しますと、

$$Ω^2-2(1-2ζ^2)Ω+1 = (Ω-(1-2ζ^2)^2+1 -(1-2ζ^2)^2・・・⑦$$

となります。よって$Ω=1-2ζ^2$が最小値となるΩです。$\frac{ω^2}{ω_0^2} = Ω$なので、

$$ω = \sqrt{1-2ζ^2}ω_0$$

が最小値となるωになりますね。

このときのピーク値は、⑦式の定数項の部分を計算すると、

$$1-(1-2ζ^2)^2 = 4ζ^2-4ζ^4 = 4ζ^2(1-ζ^2)$$

⑥式の分母のルートの中身が上式になるわけなので、

ピークの値を$X_{max}$とすると

$$X_{max}=\frac{f}{2ζω_0^2\sqrt{1-ζ^2}}$$

ζについて分母にあるので、 ζが小さいほどピークは鋭くなりますね。

ということで、共振状態の振幅と角振動数ωの関係は下図のように書けます。

簡単のために$ω_0=50、f=1$で計算しています。

ω=50の近くに共振ピークがありますが、実は少し低周波数側へピークシフトしています。

ピーク周波数は$ω = \sqrt{1-2ζ^2}ω_0$となるので、減衰の効果で低周波数側へシフトするのですね。

この式からわかるように、$ζ>\frac{1}{\sqrt{2}}$となると、解がなくなり、共振しなくなります。

計算結果から、ちゃんと共振のピークが導出できました。

まとめ

本記事では計算がメインなのでここで終わりです。

一度計算すると、理解が深まると思いますので、参考にして計算してみてください。

それではまた。

参考文献

振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎④-変位加振・地動加振・調和地動について強制振動との違いも解説

1次元の強制振動における共振の計算 減衰がある場合の挙動について

減衰のある振動の運動方程式を解く

減衰のある自由振動の運動方程式

減衰のある強制振動の運動方程式

微分方程式を解く

同次方程式の一般解

特殊解を求める

一般解から振動の様子を見る

まとめ

参考文献

1次元の強制振動における共振の計算減衰がある場合の挙動について