振動・波動の基礎 強制振動おける共振の計算 減衰無し

大学物理 振動工学

1次元の強制振動における共振の計算 減衰が無い場合は無限大に発散する

Google ad

強制振動における共振の計算について詳細です。

本記事をおススメする人

  • 共振のイメージはついたけど、数式的にもっと深く知りたい人
  • 運動方程式が解けず、共振の式が導出できない人
  • 仕事で構造物の設計をする人、大学で振動の研究をしはじめた人

強制振動の共振については下記の過去記事を参考にしてください。

参考記事

振動・波動の基礎　③強制振動と共振について

なお、微分方程式を解く必要がありますので、最低限の大学数学の知識を必要としますが、できるだけ簡潔にわかりやすく解決します。

動画でも解説していますので、是非参考にしてください。

強制振動の運動方程式を解く

単振動の式

まずは外力が働いていない場合、バネにつながれたモデルの単振動の式です。

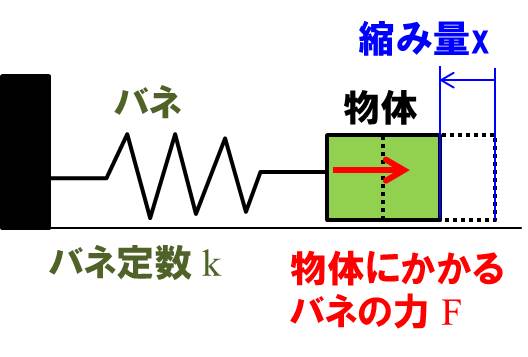
下記のようになりますね。

$$m\ddot{x}=-kx$$

この式については過去の記事で解説していますので、参考にしてください。

参考記事

振動・波動の基礎①-古典的な調和振動子（単振動）

強制振動の運動方程式

この式に強制振動を加えます。

外から周期的な力、\(Fcosωt\)というものを付け加えます。

ちなみに周期的外力は\(Fsinωt\)でも、解き方は同じです。

イメージとしては、手でバネにずーっと力を与え続けるようなイメージです。

$$m\ddot{x}=-kx + Fcosωt$$

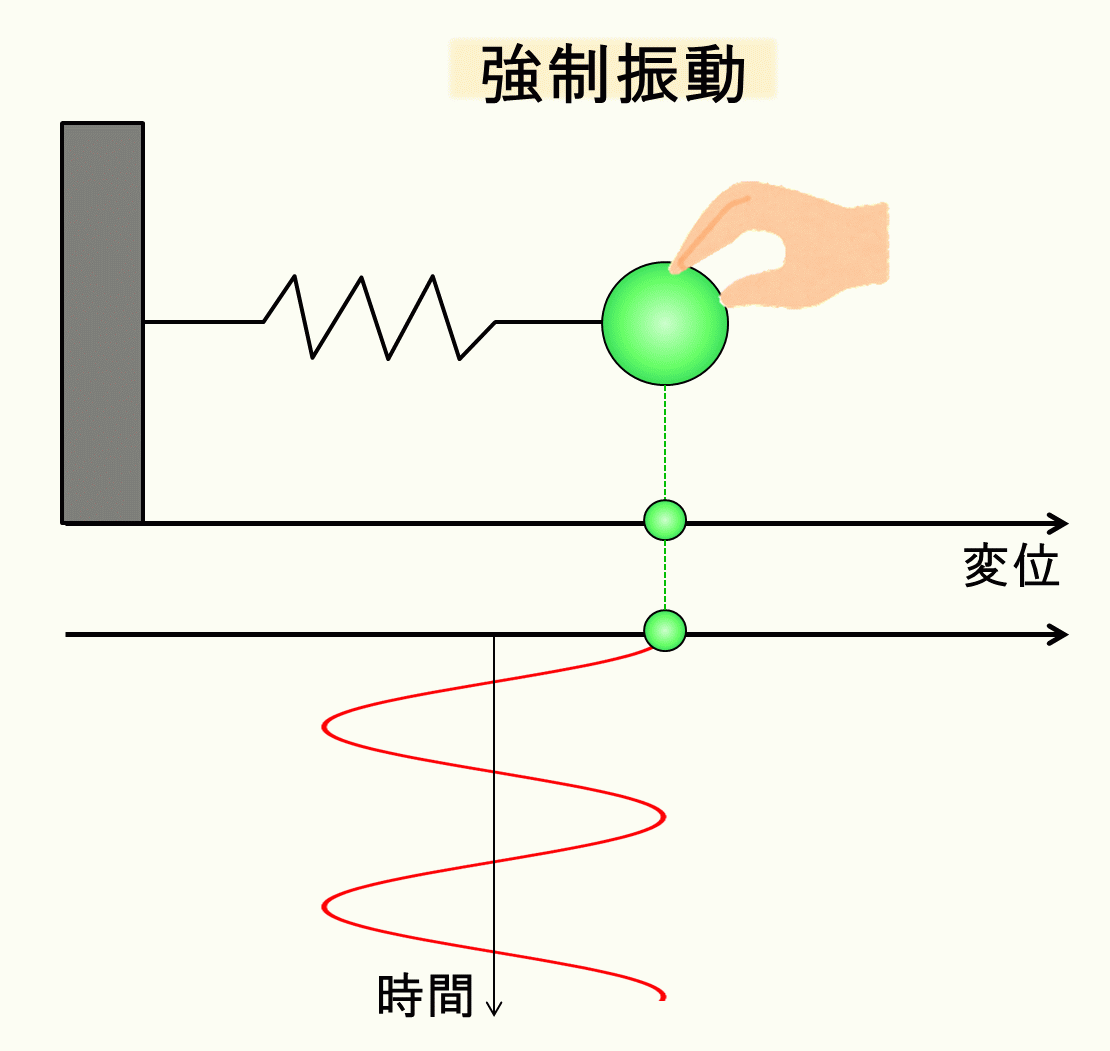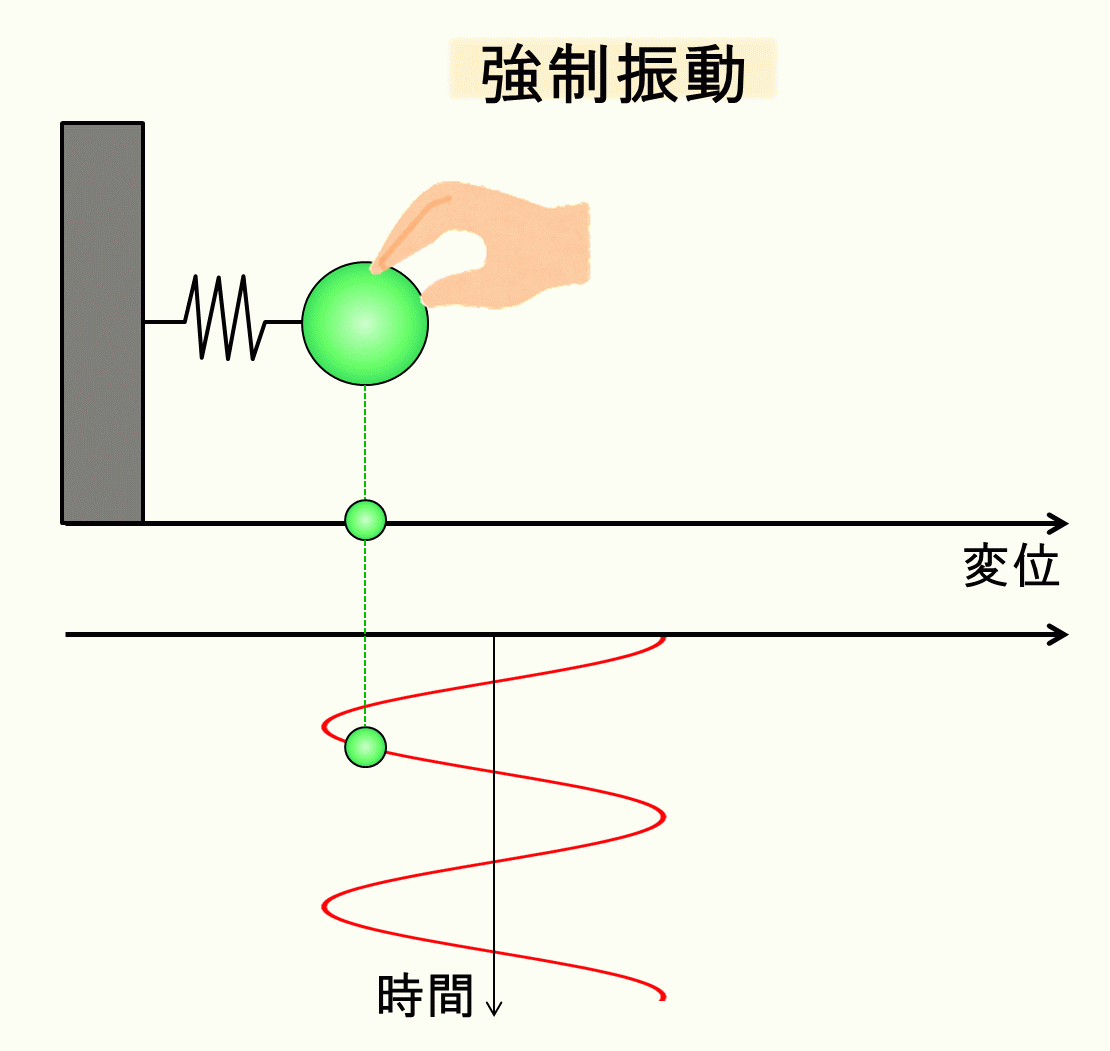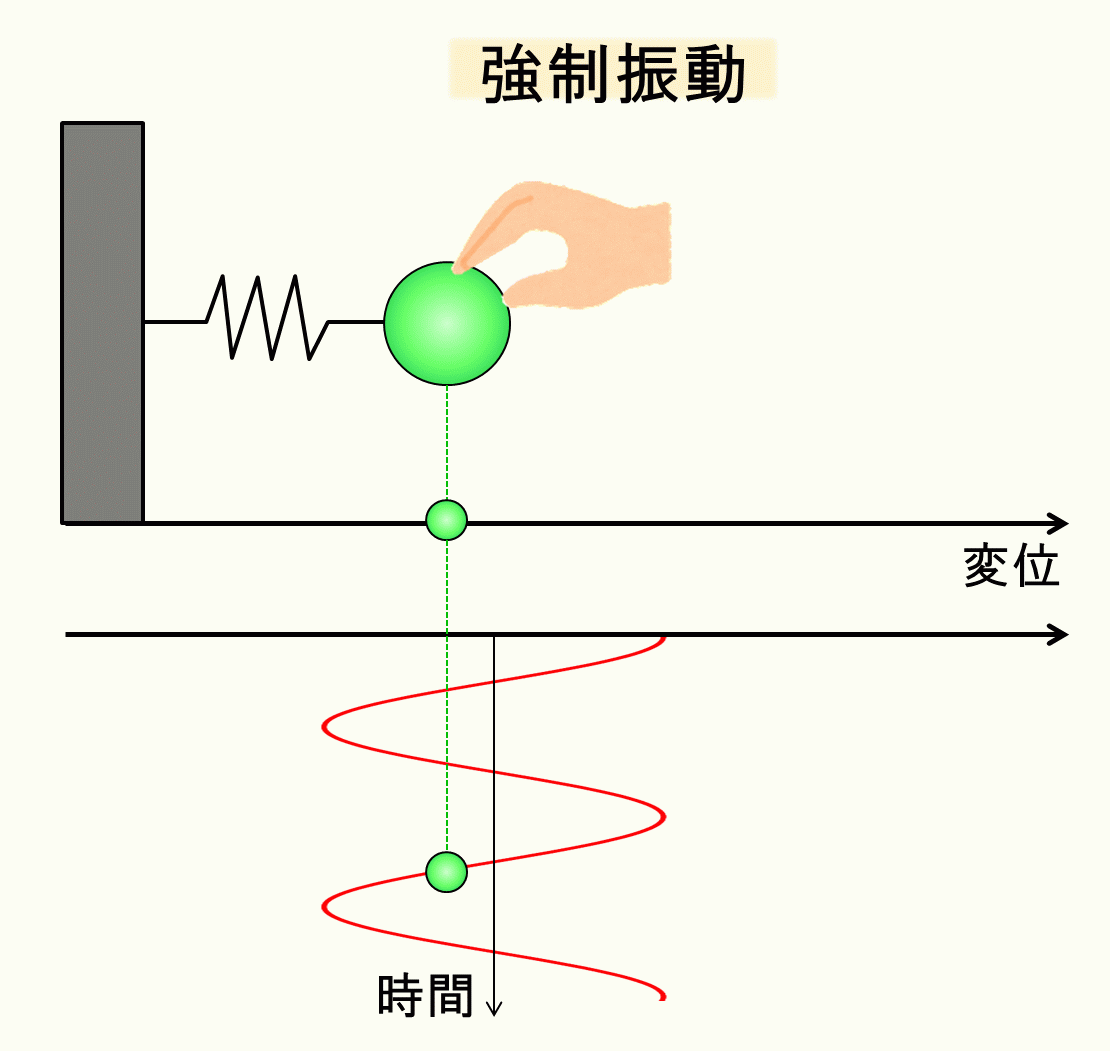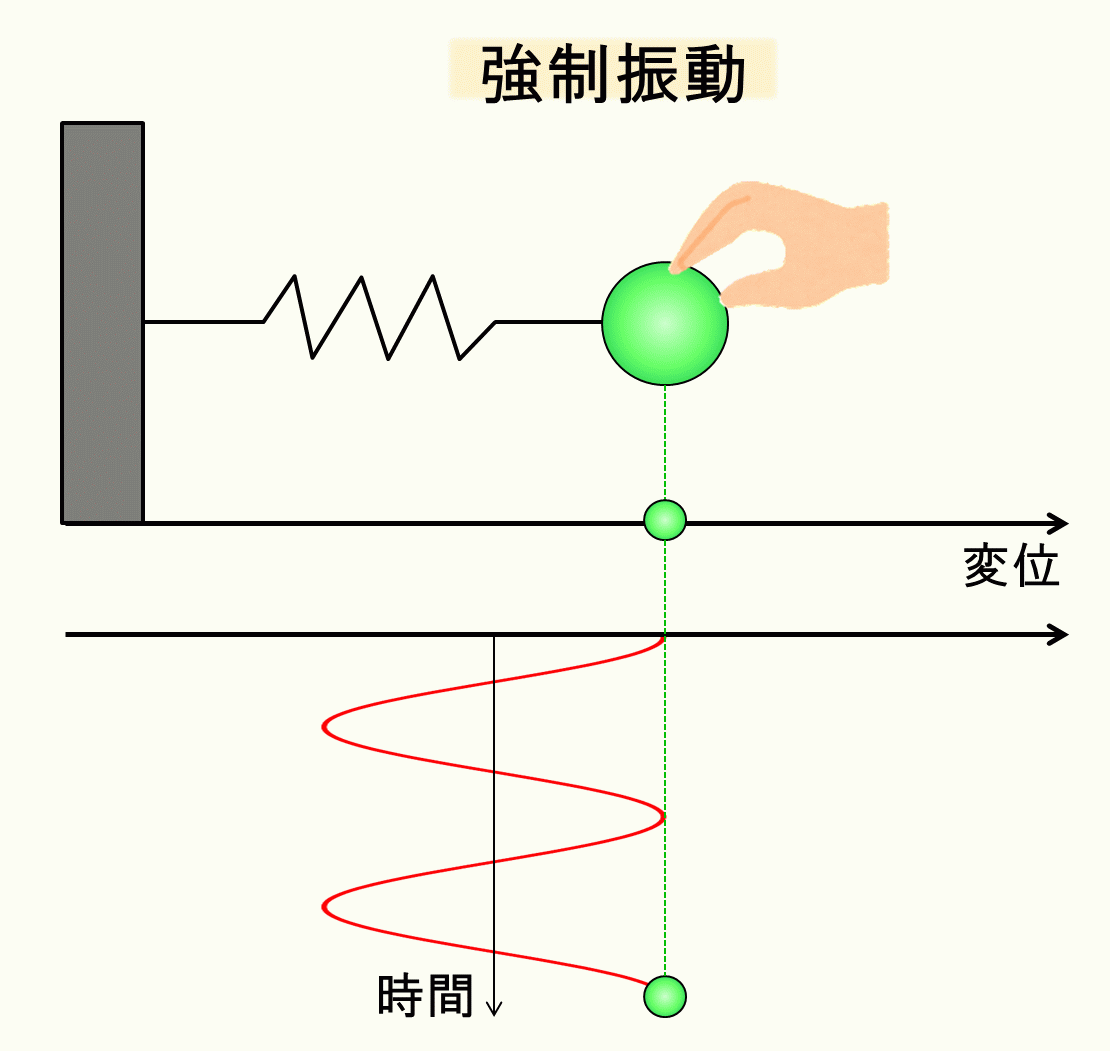
これを両辺\(m\)で割って整理します。

$$\ddot{x}=-ω^2_0x+fcosωt$$

$$ただし、ω_0=\sqrt{\frac{k}{m}}、f=\frac{F}{m}$$

この微分方程式を解きましょう。

非同次方程式の一般解

強制振動の運動方程式は２階非同次線形方程式ですので、下記のような形が一般解となります。

一般解 = 同次方程式の一般解 + 非同次方程式の特解

同次方程式は斉次方程式とも呼びます。

右辺＝ゼロの微分方程式が同次方程式なので、同次方程式の一般解というのは、自由振動の場合の解になります。

今回の場合、減衰もない状態ですので、外力が働いていない単振動の一般解になります。

つまり、\(m\ddot{x}=-kx\)の一般解ですので、\(Asinω_0t+Bcosω_0t\)ですね。

もしくは三角関数の合成を使用して\(Asin(ωt+φ)\)となります。

これは過去の記事で解いていますので参考にしてください。

自由振動

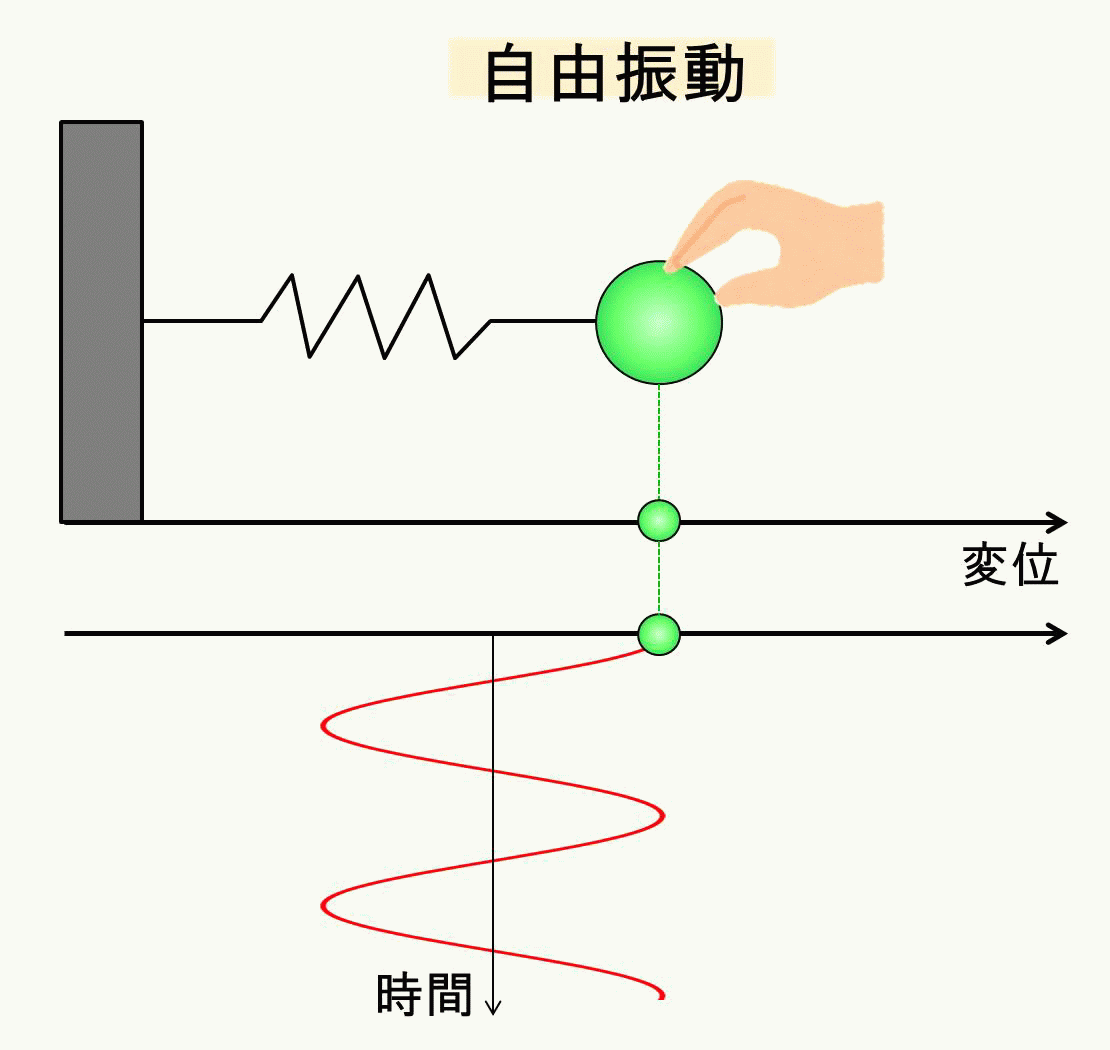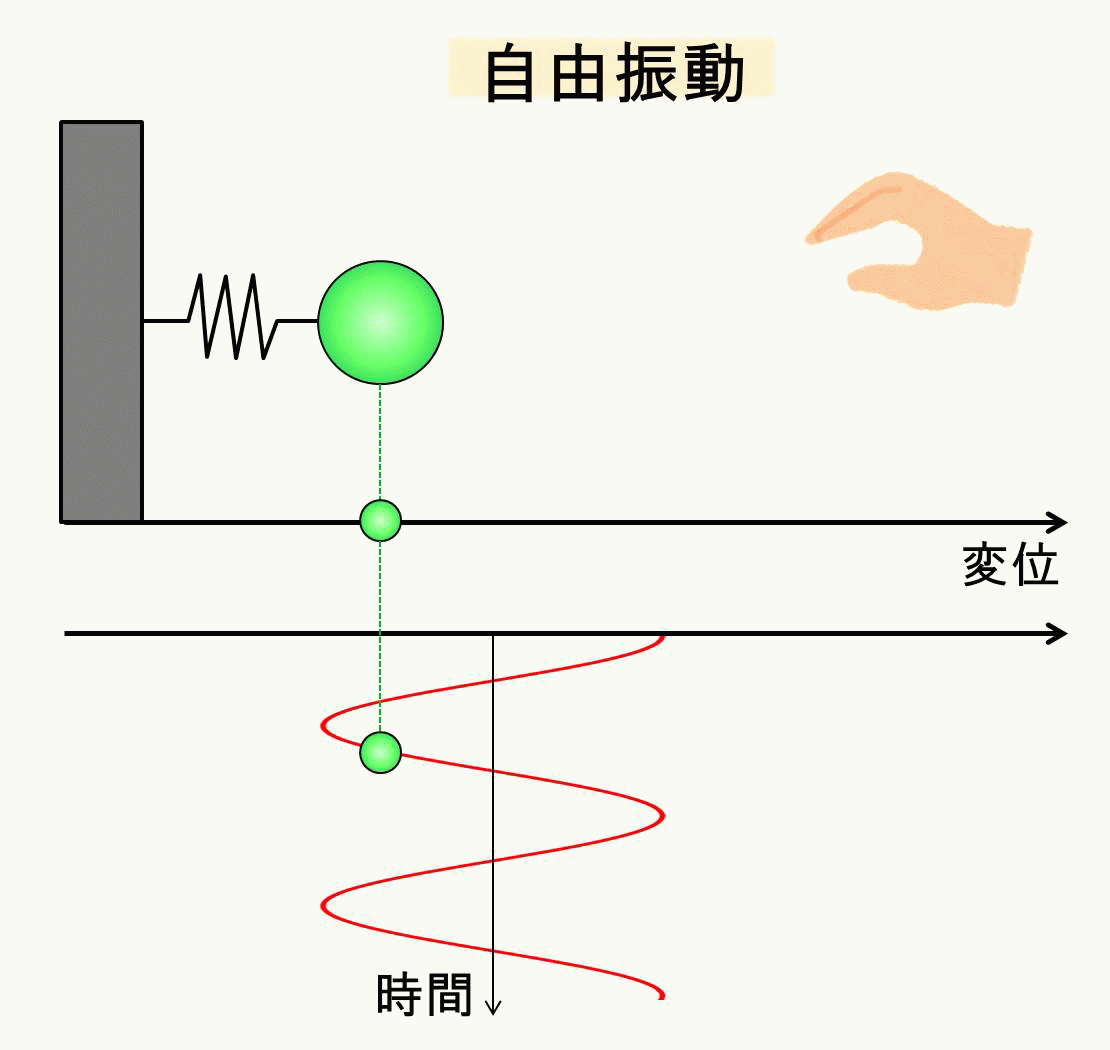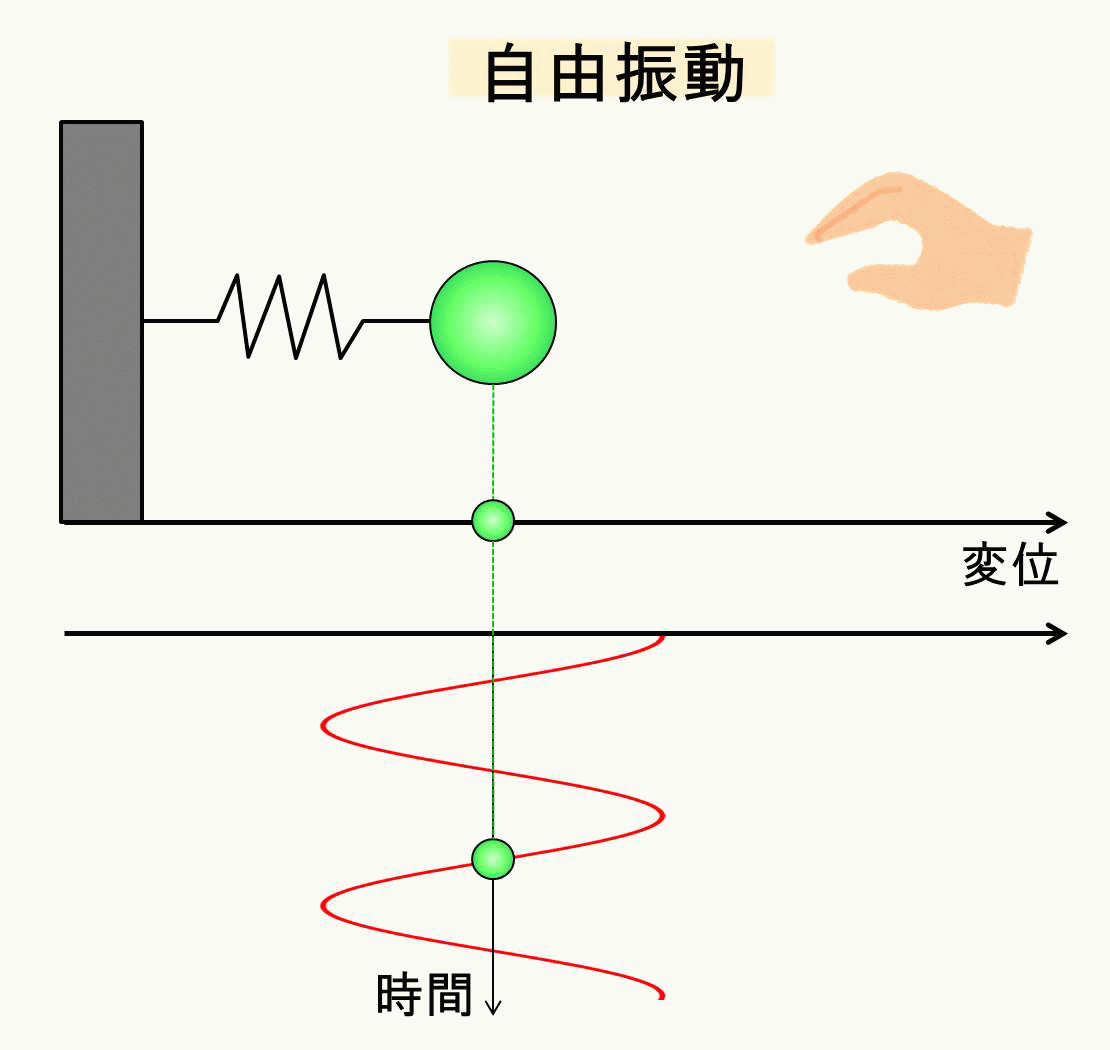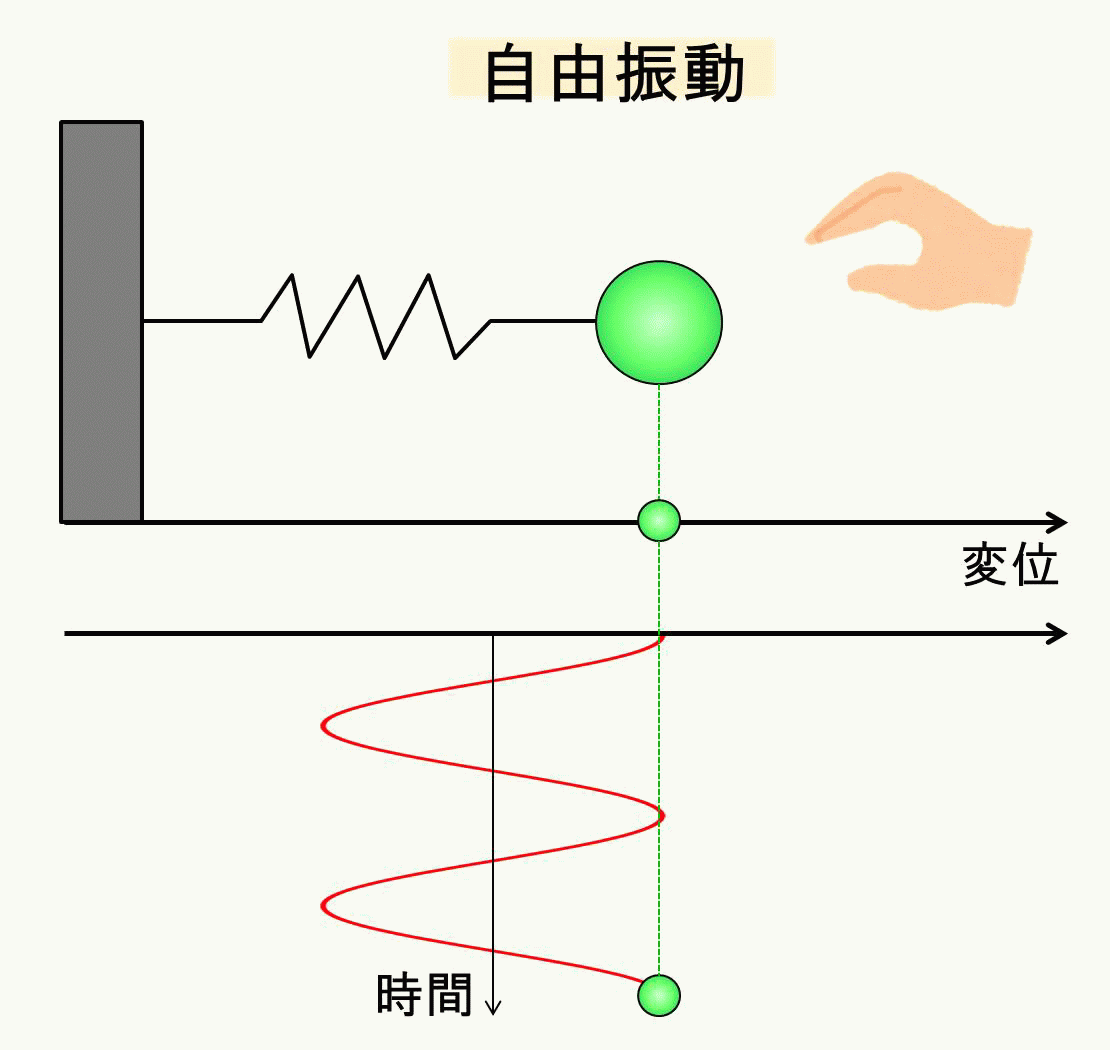
自由振動のイメージはこのような図になりますね。

非同次方程式の特解

では、次に非同次方程式の特殊解です。

$$\ddot{x}=-ω^2_0x+fcosωt$$

左辺と右辺を見比べて、2回微分したものが微分する前の形と同じものなので、三角関数を特殊解として仮定できそうですね。

さらに、\(fcosωt\)がついていますので、三角関数の中でもcosを使う方が簡単そうです。

ということで、特解を\(x=acosωt\)として、微分方程式に代入します。

$$-aω^2cosωt = -aω^2_0cosωt+fcosωt$$

\(cosωt\)を両辺から消去して、

$$-aω^2=-aω^2_0+f$$

となるので、

$$a=-\frac{f}{ω^2-ω^2_0}$$

特解\(x\)は

$$x=\frac{f}{ω^2_0-ω^2}cosωt$$

となります。

非同次方程式の一般解に初期値を与えて変形

これでめでたく同次方程式の一般解と、非同次方程式の特解がわかりましたので、非同次方程式の一般解は下記となりますね。

一般解 = 同次方程式の一般解 + 非同次方程式の特解

$$x(t) = \color{magenta}{Asinω_0t+Bcosω_0t }\color{red}{+\frac{f}{ω^2_0-ω^2}cosωt}$$
 
もしくは単振動の一般解部分を三角関数の合成をして、
 
$$x(t) = \color{magenta}{Asin(ω_0t+φ) }\color{red}{+\frac{f}{ω^2_0-ω^2}cosωt}$$
 

一般解はわかったけど、三角関数がたくさんあったら全然イメージつかないよ～！

苦手君
デルタ先生

じゃあ、もう少し具体的にしてみて、式を簡単にしてみよう。

確かにこのままだと、\(A\)とか\(B\)とかわけのわからない定数が存在して、イメージがつきにくいですね。

\(A、B\)を求めるために、\(t=0\)のときの初期状態を仮定してあげましょう。

物体の初期の位置と速度をゼロとします。

式的には、\(x(0) =0、\dot{x}(0)=0\)です。

イメージとしては、『強制振動を与える前は、ぜ～んぜん動いてません』、っていう状態です。

さて、この場合、一般解はどうなるかを計算すると、

$$x(0) = B +\frac{f}{ω^2_0-ω^2} = 0$$
$$\dot{x}(0) = A =0$$

です。\(t=0\)なので、\(x(0)\)は\(cos\)の項が、\(\dot{x}(0)\)は\(sin\)の項が残りますね。\(B\)については

$$B=-\frac{f}{ω^2_0-ω^2}$$

となりますので、\(A=0\)と共に一般解に代入しましょう。

$$x=-\frac{f}{ω^2_0-ω^2}cosω_0t+\frac{f}{ω^2_0-ω^2}cosωt$$

\(cos\)の係数が同じなので整理すると、下記となります。

$$x=\frac{f}{ω^2_0-ω^2}(cosωt-cosω_0t)$$

共振現象

さてここで、共振現象を考えます。

共振とは モノの固有振動数と外力の振動数が一致することを指しますので、 \(ω→ω_0\)と極限をとった場合を考えます。

少し見通しが悪いので、三角関数部分を和積の公式で変換します。

$$x = \frac{2f}{(ω+ω_0)(ω-ω_0)}sin\frac{ω+ω_0}{2}t・sin\frac{ω-ω_0}{2}t$$

\(ω-ω_0=Δω\)として、\(\frac{Δω}{2}\)で整理すると、

$$x = \frac{f}{(ω+ω_0)}sin\frac{ω+ω_0}{2}t・\frac{sin\frac{Δω}{2}}{\frac{Δω}{2}}t$$

\(ω-ω_0=Δω\)なので、\(ω→ω_0\)と極限をとったとき、\(Δω→0\)となります。

ここで、上式の中にある、

$$\frac{sin\frac{Δω}{2}}{\frac{Δω}{2}}t$$

の部分は、\(Δω→0\)の極限をとると、ロピタルの定理で\(t\)となります。

(これは\(x→0\)のとき、\(\frac{sinx}{x}→1\)となるからです。)

よって、\(ω→ω_0\)と極限をとったとき、

$$x = \frac{ft}{2ω_0}sinω_0t$$

となります。

この式を見てみると、振幅部分が\(ft\)となっていますので、時間が経てば経つほど、振幅が大きくなることを示しています。

時間を無限大にしてしまうと、振幅も無限大、つまり、とてつもなく大きな振動に発達する、ということです。

これが共振現象です。グラフを書くと下記のようになります。

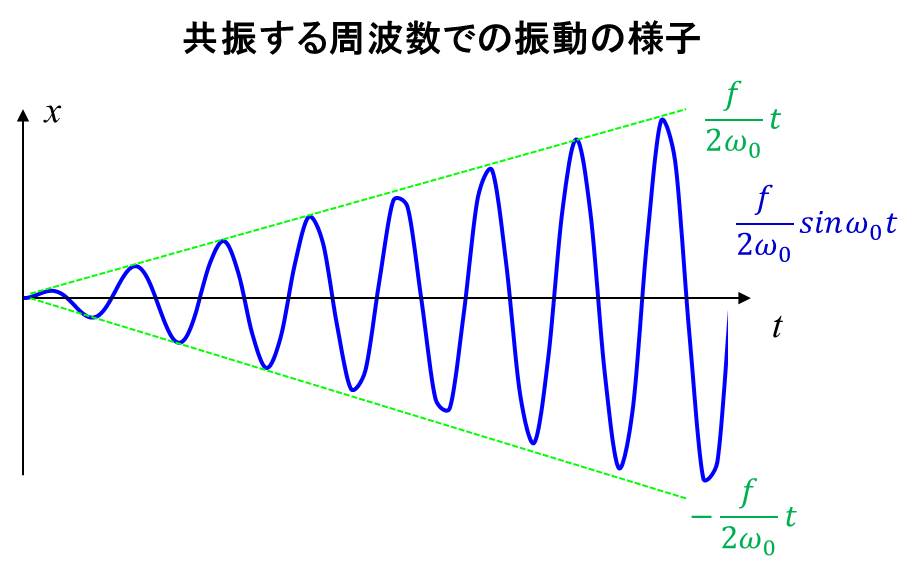
これは外力の周波数ωが、振動するモノの固有振動数\(ω_0\)と一致するときのグラフです。

tが増加すると、だんだん変位量xが大きくなっていますね。

\(x=±\frac{f}{2ω_0}t\)の間の領域で振動します。

まとめ

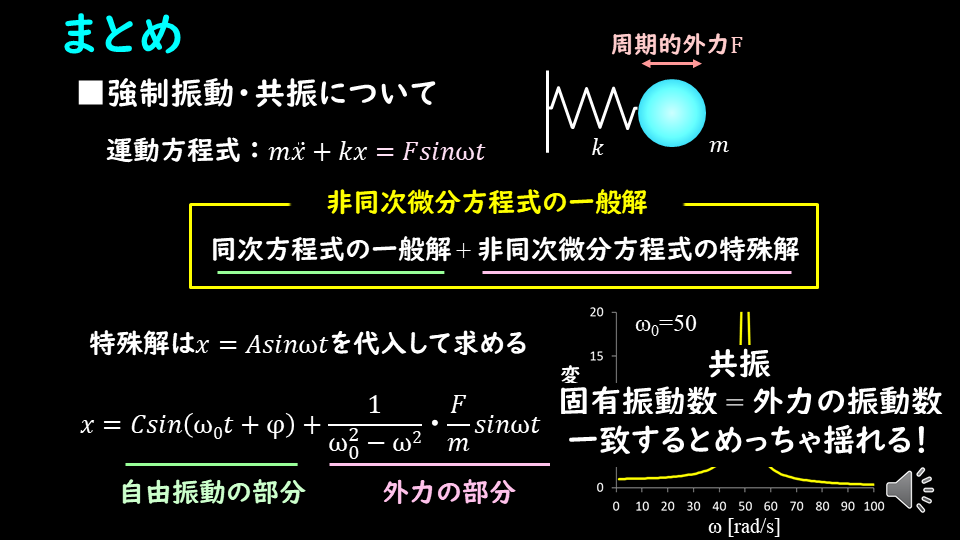
※上記スライドでは、周期的外力が\(sin\)なので、特殊解を求める際にも\(x=Asinωt\)となっています。

計算についてかなり詳しく書きましたが、大学生レベルの数学知識が必要となります。

微分方程式の解き方の基礎は下記の記事を参考にしていただければと思います。

微分方程式の基礎　超初心者向け-①微分方程式についてやさしく解説

参考文献

  • 振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
  • 機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎④-変位加振・地動加振・調和地動について 強制振動との違いも解説

-大学物理, 振動工学
-, , ,