[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]浮力って水の中で浮かぶ力だよね？なんで物によって浮いたり沈んだりするの？[/voice]
[voice icon="https://deltapower.site/wp-content/uploads/2020/09/にっこり右側.jpg" name="デルタ先生" type="r"]浮力や水圧が関係しているんだけど、浮くかどうかに焦点を当てて解説するね？[/voice]
『どれが浮いてどれが沈みますか？』
教育番組とかクイズ番組とかでも定番ですね。
浮力で押さえておくポイントは下記です0。
[box class="pink_box" title="浮力のポイント"]
①物体の下側に流体があったときに浮力は発生する（浮力は水圧の仲間）
②浮力は押しのけた流体の重さで決まる
③浮くか沈むかは、浮力と下向きの力とのケンカで決まる。
[/box]
これらをしっかり理解しておけば、浮力に対する理解がぐっと深まります。
[box class="green_box" title="本記事をおススメする人"]
- 力学を学び始めた方で、浮力・水圧がよくわかっていない人
- 何が浮いて何が沈むかがよくわからない人
- 授業の予習でどんな感じかをつかみたい人
[/box]
目次
浮力の発生原因
浮力の発生原因 = 水圧の上下の差
まずは浮力がなぜ発生するかについて解説しましょう。
これには水圧について理解する必要がありますので水圧の解説をします。
水圧
水圧とはその名の通り、水から受ける圧力というイメージです。
では、下記のように箱を水の中に沈めたとき、どのような水圧がかかっているでしょうか？
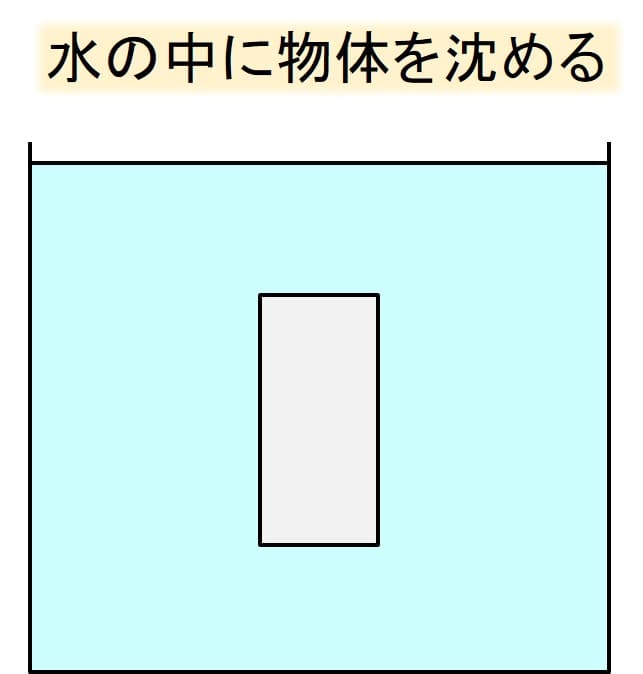
水圧は物体全面に発生しており、潜っている部分が深くなればなるほど大きくなります。
言葉では知っている人が多いかもしれませんが、どういう原理か、下記のアニメーションで理解してみましょう。
まず、水を〇がいっぱい敷き詰められたモデルに書き換えます。
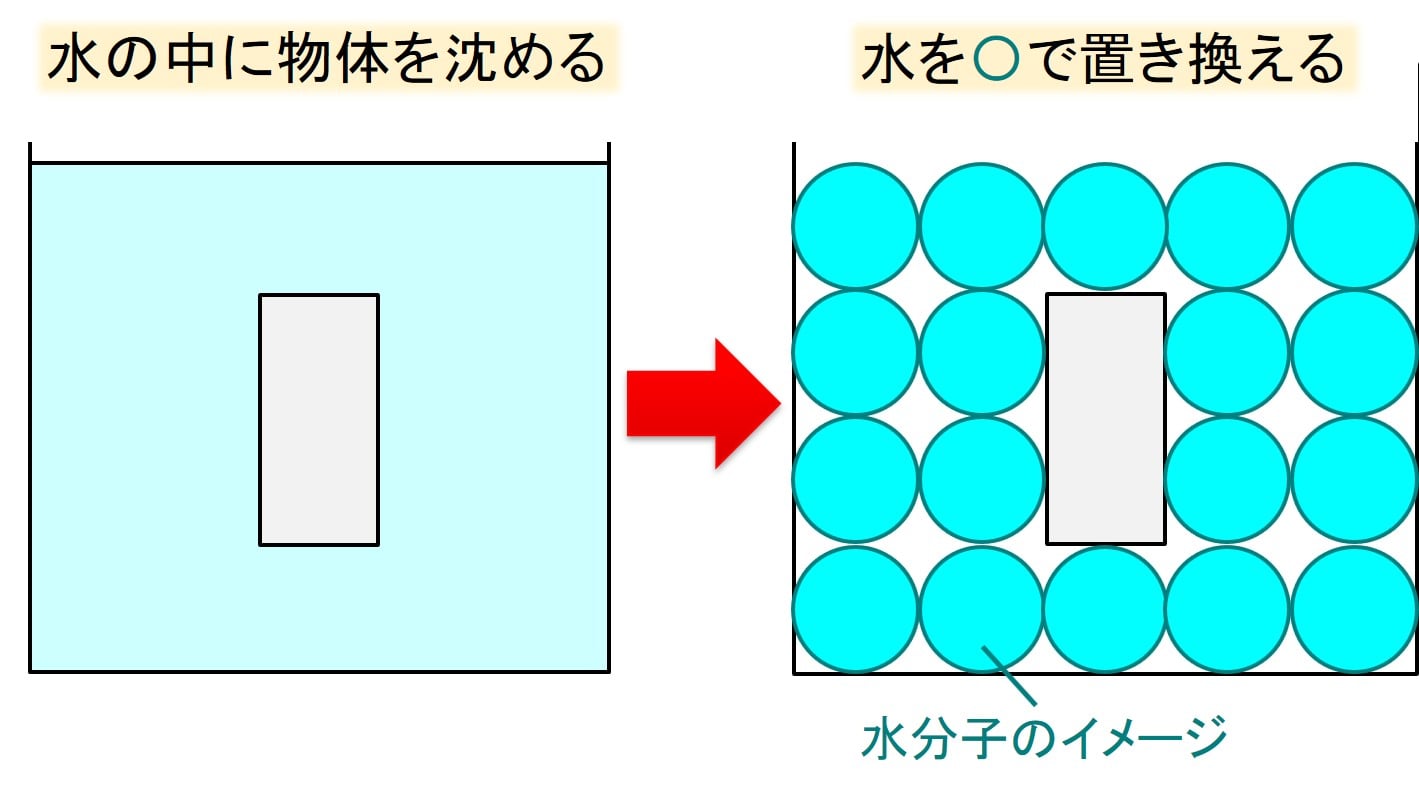
水分子なので、重力で下方向に力がかかるわけですが、水分子は横に水分子がいないとぐにゃっと変形してしまいます。
しかし、実際は水分子の横には同じ水分子や壁があるわけで、横向きに変形できません。
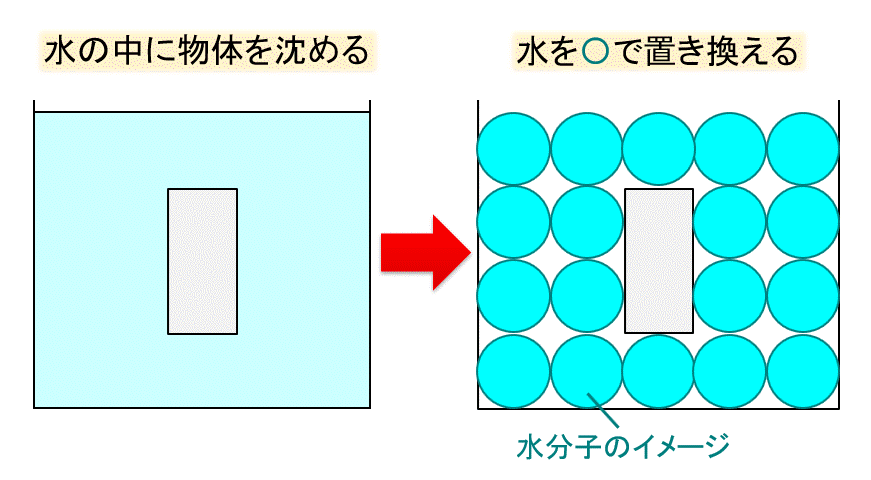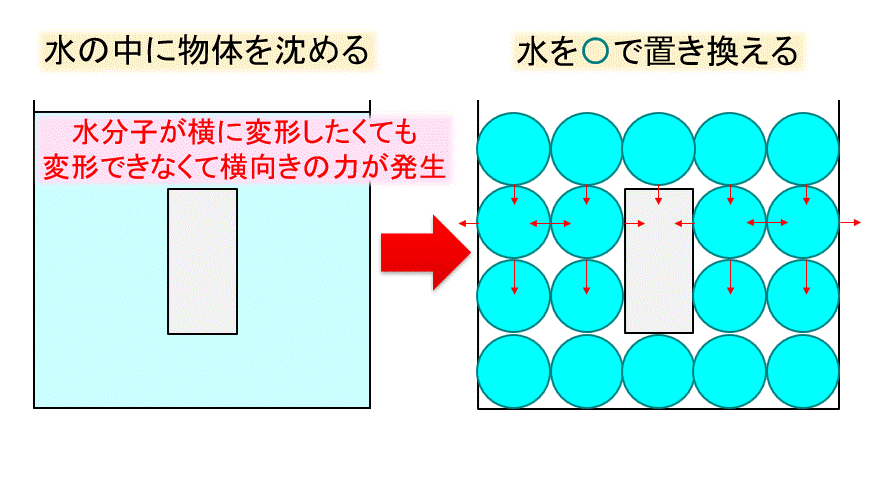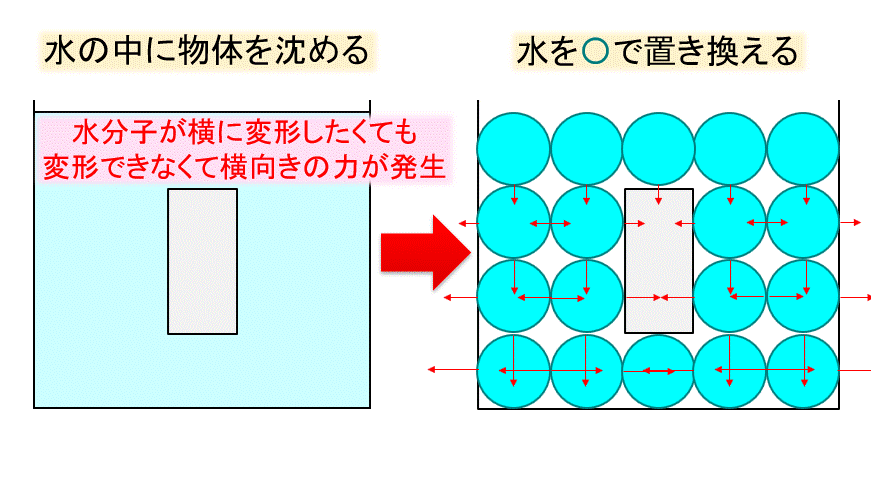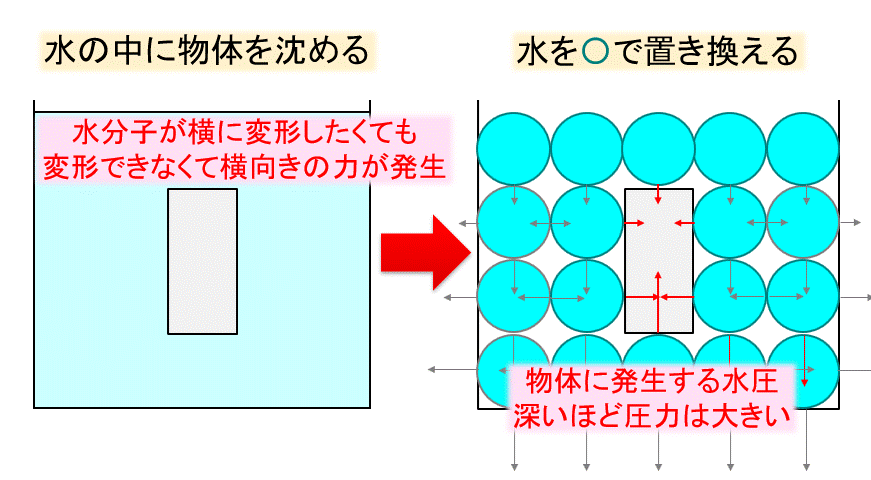
ですので、変形しようと隣の水分子や壁と押し合う力が発生し、左右上下の力がつりあいます。
一番下の物体の真下にある水分子は、左右から押されて、上下に伸びようとしますが、上に物体、下に底があるので、これも変形できません。
ここでも上下の力が発生し、物体の真下にある水分子は物体を押し上げる方向の力を生みます。
よって水圧は深くなればなるほど大きくなるわけです。
しかも、物体に対して全方向から押されます。
浮力と水圧の関係
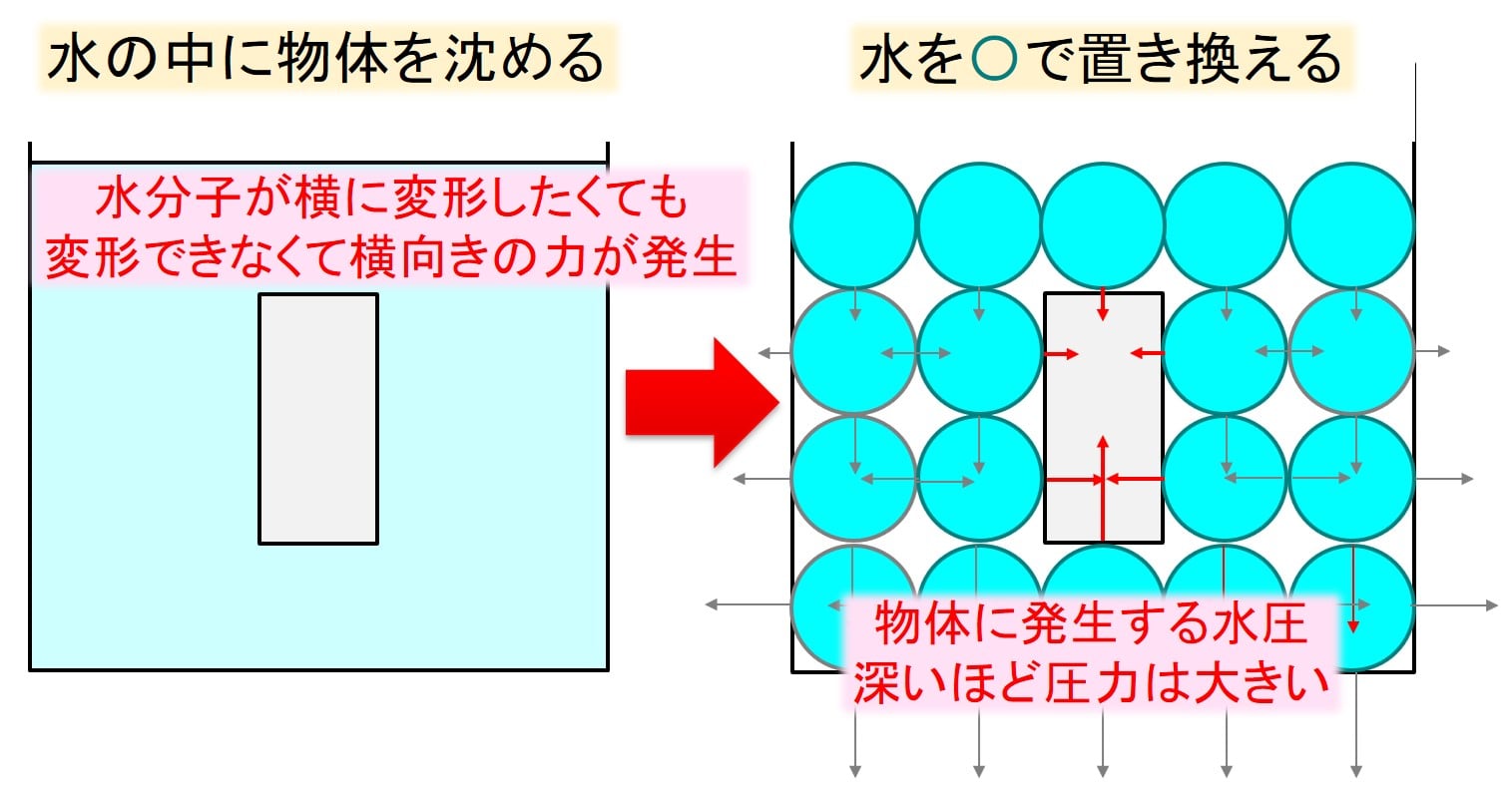
先ほどの図をもう一度見てみましょう。
縦方向の力の関係に注目します。
物体を下に押す圧力と、上に押し上げる力を比べてみると、上に押し上げる力の方が大きいですね。
これは深くなればなるほど水圧が大きくなるからです。
つまり、水の中に物体を入れると必ず上向きに力が発生します。
以上、浮力の定義から『上から下向きにかかる水圧による力』-「下から押し上げる水圧による力』で浮力が求まります。
浮力が発生しないケース
浮力が発生しないケースがあります。
例えば図のような状態です。
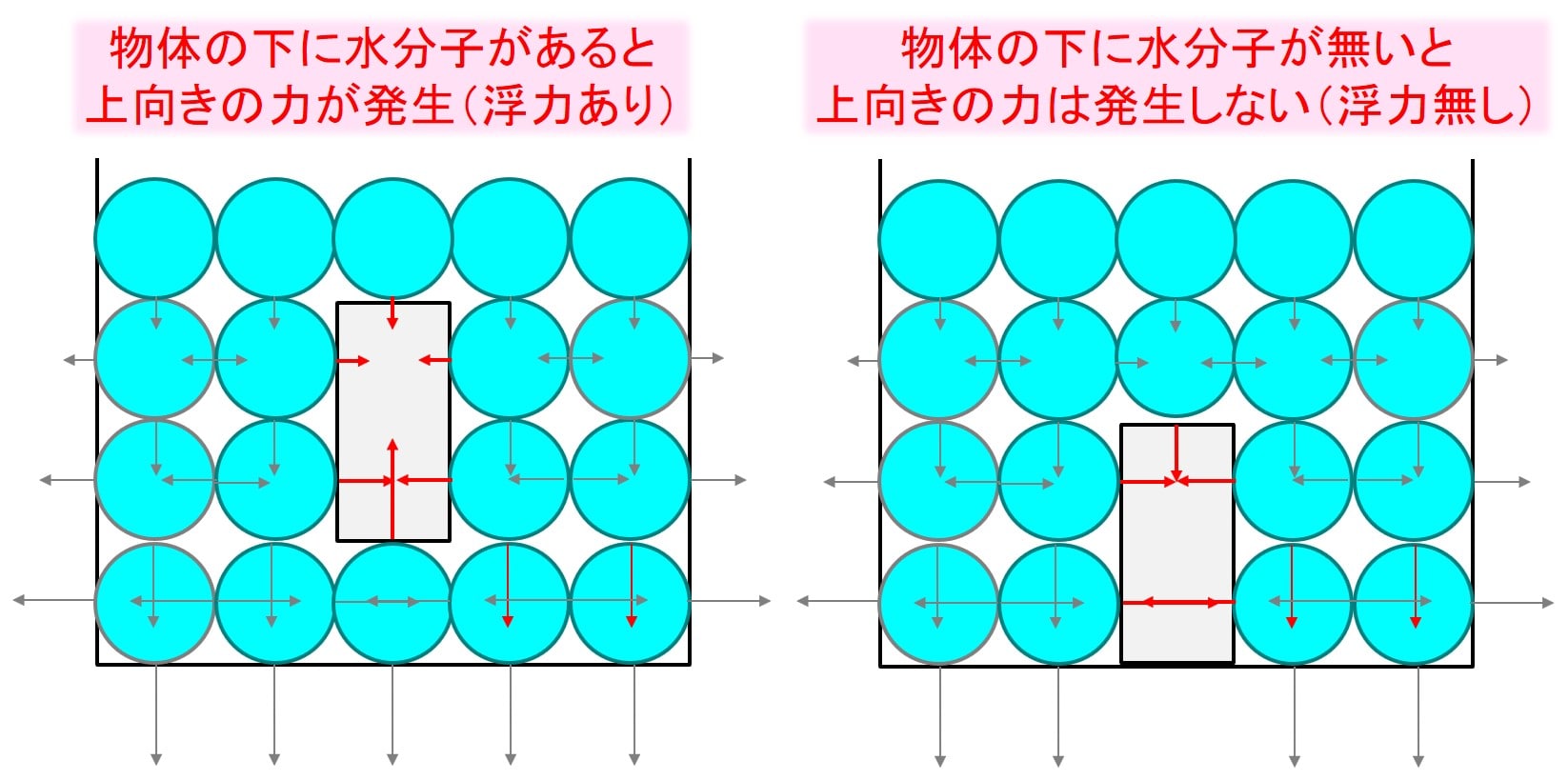
箱と床の間に水が入り込んでいない状態では、箱に浮力が発生しません。
浮力は『上から下向きにかかる水圧による力』-「下から押し上げる水圧による力』なので、
箱の下に水が無ければ浮力は発生しません。
浮力の式の導出
浮力の式は下記で求まります。
$$F=ρVg$$
Fが浮力、ρが水の密度、Vが押しのけられた水の体積、gは重力加速度です。
アルキメデスの原理とも言います。
それでは浮力を導出する前に水圧の式を導出します。
水圧の式
下の図のように、水の中にとある面を作って、そこに発生する水圧を考えます。
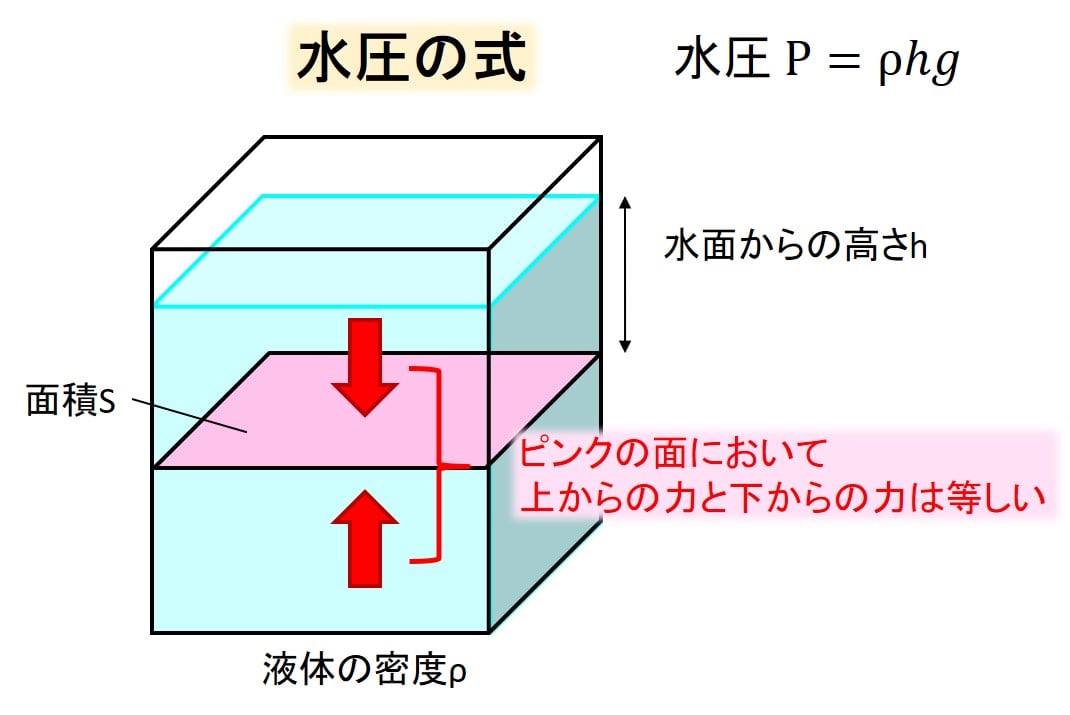
ここの面積をSとして、上からの圧力と下からの圧力が等しい状態を作ります。
（厚みをめっっちゃ薄くすると、上からの力と下からの力が同じになる、というイメージです）
上からの圧力は、先ほどのモデルを考えると、水が重力によって上から押す力ですね。
面の上にある水の密度をρ、沈めた面と水面との距離をhとすると、体積はh×Sで求まります。
密度と体積を掛け合わせると質量となるので、上から押す力Fは
$$F=ρ×h×S×g$$
この力が下からの力と等しいので、下からの力もFとなります。
水圧Pは力Fを面積Sで割ればよいので、
$$P=ρ×h×g$$
水圧は水面からの距離hに比例することが分かりますね。
浮力の式
さて、次に浮力を導出しましょう。
水の中に物体を入れて、浮力とつりあっている状態を作ります。
物体は直方体で、上面の面積をSとします。
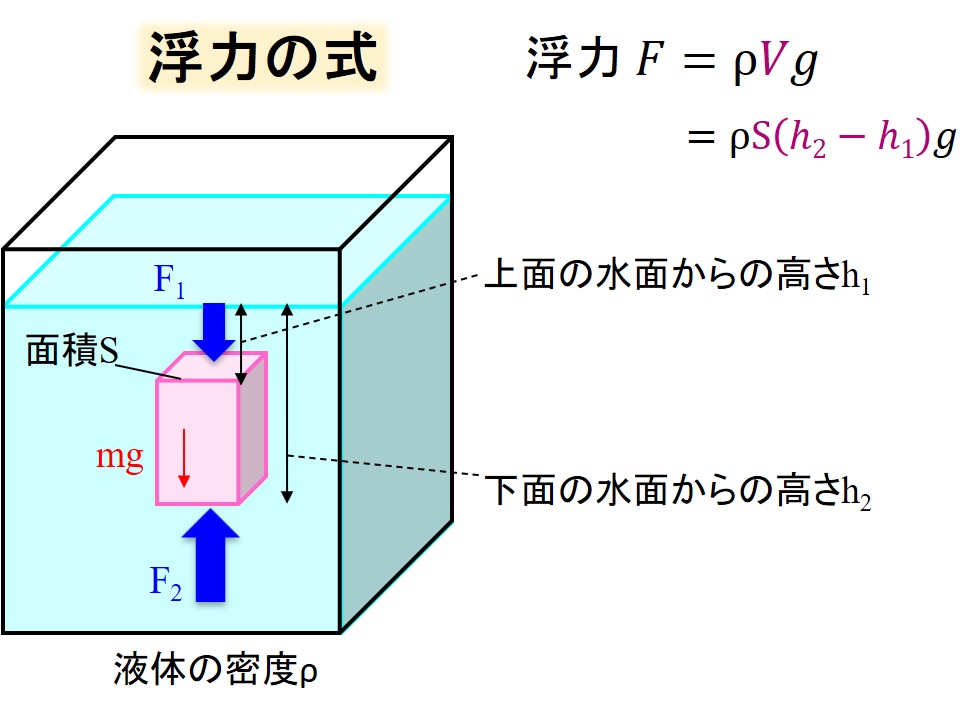
物体の質量をmとすると、物体には重力mgと上からの水圧$P_1$、下からの水圧$P_2$が発生しています。
$P_1$は物体の上面と水面の距離を$h_1$とすると、$P_1=ρh_1g$で、
$P_2$は物体の下面と水面の距離を$h_2$とすると、$P_2=ρh_2g$となります。
これら$P_1$と$P_2$は圧力なので、両辺に面積Sをかけることでそれぞれの力が求まります。
上からの水の力を$F_1$、下からの水の力を$F_2$とすると、
$$F_1=ρSh_1g$$
$$F_2=ρSh_2g$$
浮力は『上から下向きにかかる水圧による力』-「下から押し上げる水圧による力』でした。
つまり$F_2-F_1$で求まりますので、浮力Fは、
$$F = ρSh_2g-ρSh_1g = ρS(h_2-h_1)g$$
となります。
ここでS(h_2-h_1)は物体の体積Vと等しいので、
$$F=ρVg$$
と、浮力の公式が求まりました。
浮力と高さの関係
あれ？浮力って深さによって変わらないの？
そうだよ、沈んだ体積で決まっちゃうから、一度全体が沈んで浮かんでこなかったら底まで沈んでしまうんだ。
浮力の式を見ると、水の中に入った体積Vが入っているだけで、全体を沈めてしまえば、水面からの距離は関係ないことがわかります。
浮力の具体例
[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]じゃあ途中まで沈めるとどうなるの？[/voice]
[voice icon="https://deltapower.site/wp-content/uploads/2020/09/にっこり右側.jpg" name="デルタ先生" type="r"]それはいくつかのケースをグラフ化して見てみようか。[/voice]
最終的には浮力と重力のケンカで、浮力が勝つと浮きます。
逆に重力が勝つと沈みます。それでは具体例を見てみましょう。
ケース① 平らな板
平な板を水の上に浮かべます。
まずは軽い板を入れてみましょう
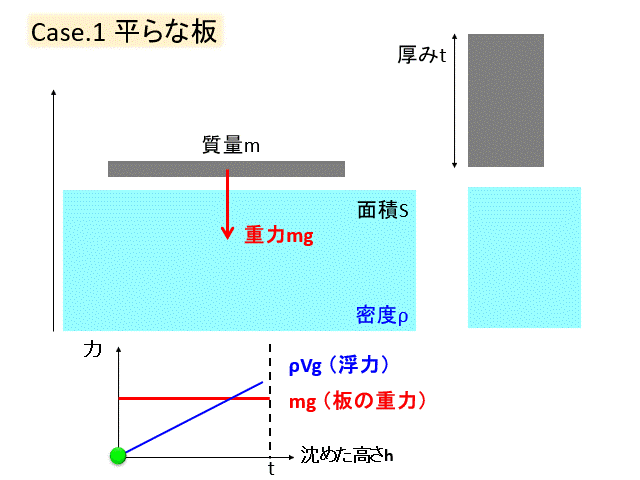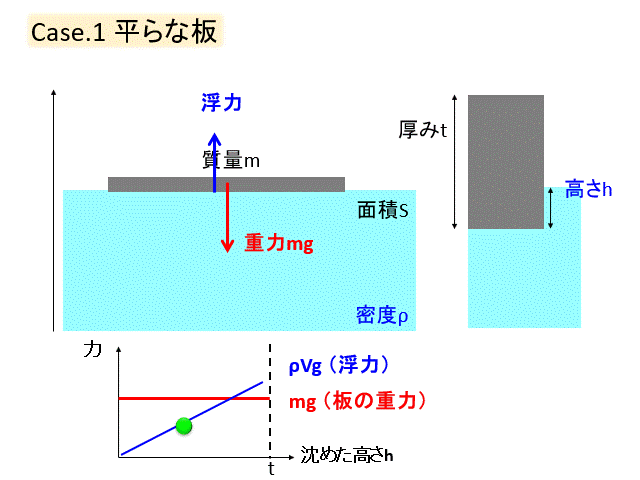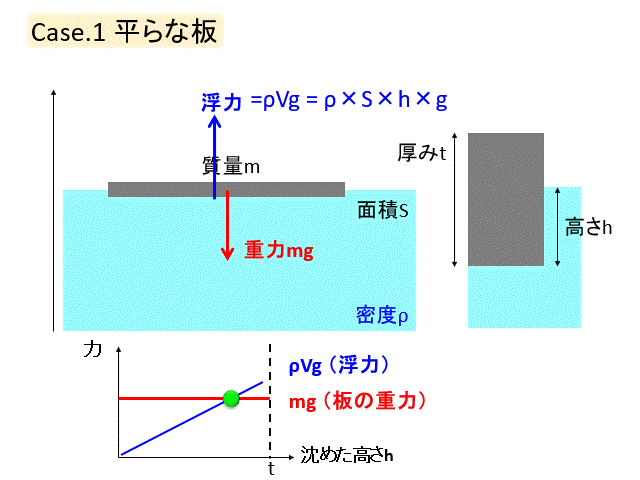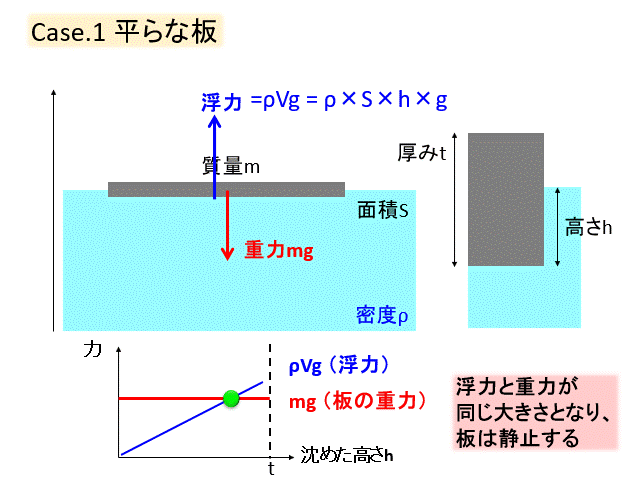
徐々に沈めていくのですが、沈めていくと水に入っている体積が増えるので、浮力は増加します。
やがて浮力と重力がつりあって、板は静止します。
次に板を少し重くしてみましょう。
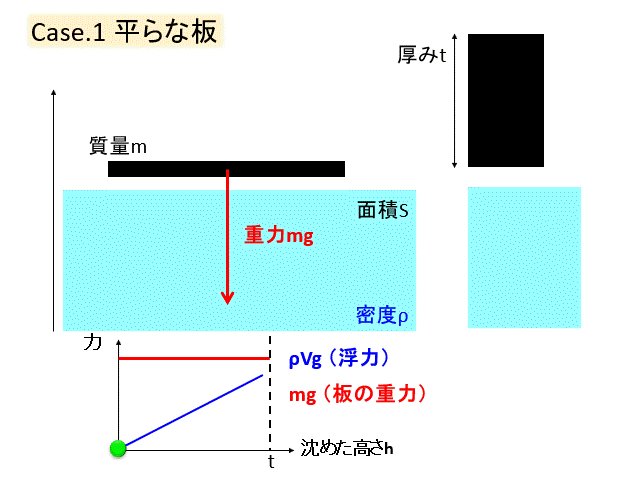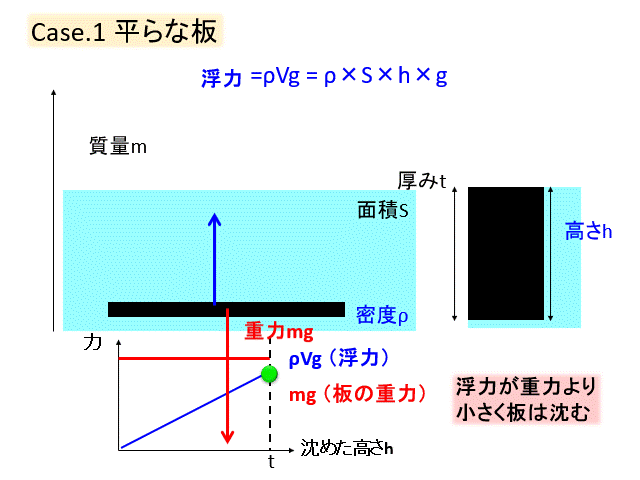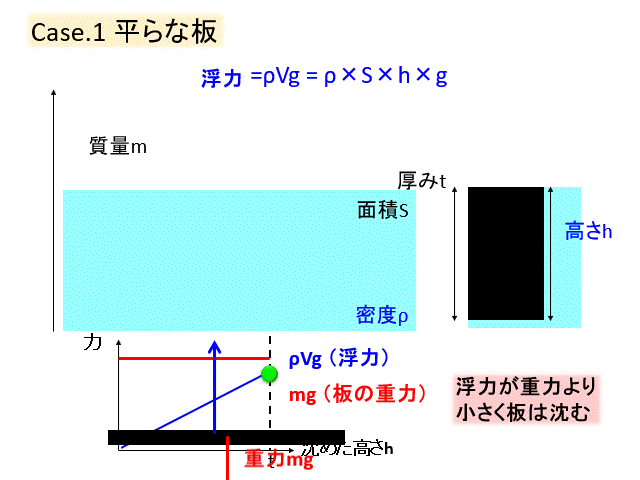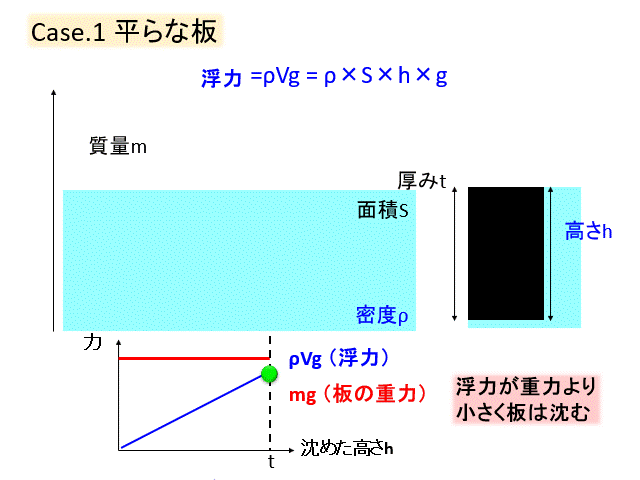
先ほどと同様、沈む体積が増えるほど浮力が増えるのですが、浮力が最大になっても板の重力とつりあうことはできず、沈んでいきます。
底を貫通して沈んでいくのはご愛敬(;^^)
ケース② 船に穴が空いた！
次のケースとして船に穴が空いて、水が入ってくるとどうなるかを考えてみましょう。
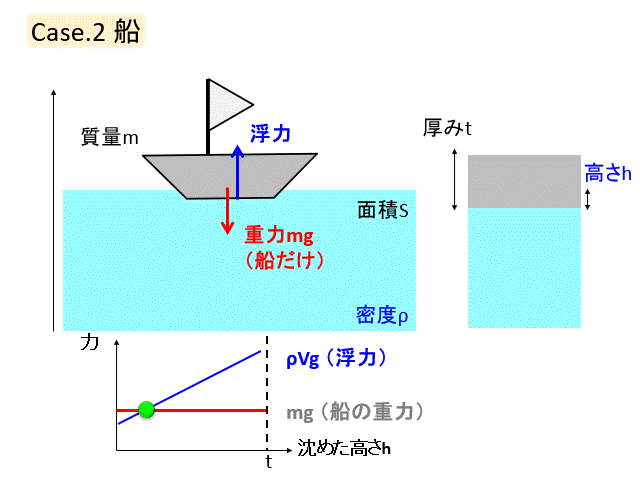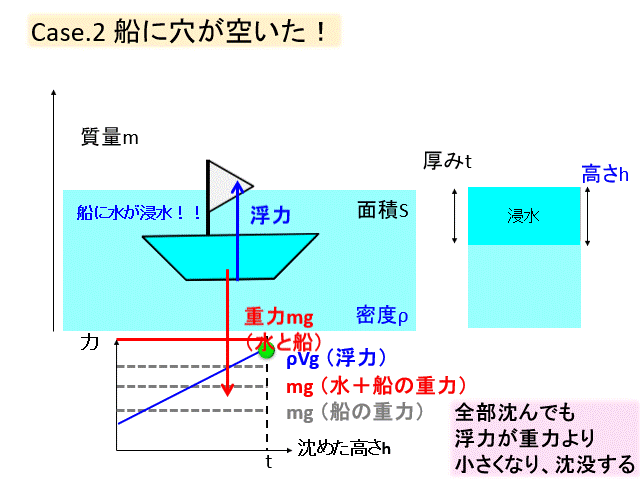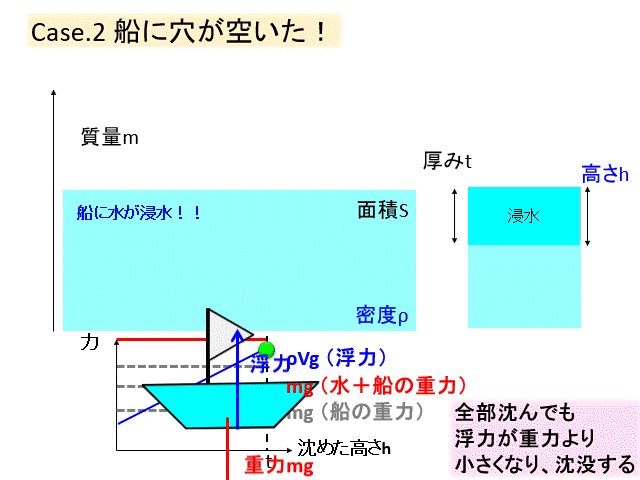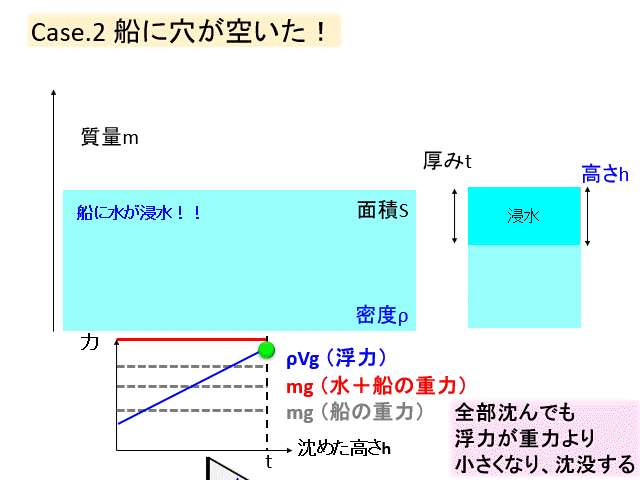
船の中は空気として、重力と浮力がつりあっている状態を考えます。
ここで船底に穴をあけて水が入ってきます。
すると水が入ってきた分、重力は増加し、船は沈みます。
沈んで浮力は増加するのですが、沈んだ分、また水が入ってくるので、また沈む、そしてまた水が入る、
沈む→水が入る→沈む→水が入る→沈む→沈む→沈む・・・
そう、水が入り込むと沈むのです。
船に穴が空いたら、真っ先に水が入ってこないように穴をふさぐなどの処置をしないと、沈没します。
タイタニック号も船底に穴が空いて沈没しましたね。
何が浮いて何が沈むのか？
浮力の式はF=ρVgで、浮くか浮かないかを沈めるのは
物体の重力と浮力のケンカ でしたね。
物体の質量をmとすると重力mgと浮力ρVgのどちらが大きいかです。
ではどんな要素で決まるかをもっと詳しく調べてみましょう。
浮かぶことを決めるパラメータ
力のつり合いから考えましょう。
重力と浮力が等しいとすると、
$$mg=ρVg$$
となって、両辺から重力加速度gを消去しますと、
$$m=ρV$$
この条件のとき、重力と浮力がつりあいます。
左辺の物体の質量mは物体の体積を$V_1$、密度を$ρ_1$とすると、
$$m=ρ_1V_1$$
となります。書き換えると、
$$ρ_1V_1=ρV$$
左辺は物体、右辺は水の質量を表しています。
ここで、物体を沈めるとき、浮力が最大となるのは、$V=V_1$なので、このときを考えると、体積Vの項も両辺から消去できて、
$$ρ_1=ρ$$
となり、物体と水の密度が等しいとき、重力と浮力がつりあうことになります。
水の密度は$1g/cm^3$なので、物体の密度が$1g/cm^3$より高ければ沈みますし、低ければ浮力が勝ってぷかぷか浮かぶことになります。
具体例 人間も浮かぶ海
密度が低い物、軽いものが浮きやすいというのはイメージが付きやすいので、例は割愛します。
具体例として、プールと海水の違いがあります。
海水には多くの塩分が含まれており、実質的に水の密度が$1g/cm^3$より高くなります。
ヨーロッパには死海という塩分濃度が非常に高い湖があり、ここでは人が浮き輪なしで浮かぶことができます。
浮くか浮かないかは、物体の密度が液体の密度より大きいか小さいかで決まる、水の場合は密度は$1g/cm^3$ということを押さえておきましょう。
まとめ
浮力と水圧について解説しました。
[box class="pink_box" title="浮力のポイント"]
①物体の下側に流体があったときに浮力は発生する（浮力は水圧の仲間）
②浮力は押しのけた流体の重さで決まる
③浮くか沈むかは、浮力と下向きの力とのケンカで決まる。
[/box]
浮力の公式はアルキメデスの原理とも呼ばれ、下記で表されます。
$$F=ρVg$$
ρは液体の密度、Vは液体の体積、gは重力加速度です。
浮力は上下にかかる水圧の差で決まる力なので、物体の下側に液体が入り込まないとき、浮力が発生しないことに注意してください。
また、物体が浮かぶかどうかは、物体と液体の密度を比べることで決まります。
よく出てくる水の密度は$1g/cm^3$ですので、$1g/cm^3$より大きい密度の物体は沈みます。
以上、盛だくさんでしたが、しっかり理解して水圧、浮力のイメージを身に付けてくださいね。