あれ?フックの法則ってバネの式だよね?材料力学で出てきた式ってなんか文字が違うんだけど・・・


本質的には同じなんだけど、高校で習ったフックの法則をもっと広い範囲で使えるようにしたのが、材料力学で学ぶフックの法則なんだ。
材料力学で習うフックの法則について解説します。
高校物理でもバネの式でフックの法則が出てきましたが、それをもっと一般的に拡張するイメージです。
難しそう・・・と思った方もいらっしゃるかもしれませんが、高校生でも理解できるように解説します。
高校生で習うフックの法則は、過去記事で解説していますので、参考にしてくださいね。
本記事ではこんな人におススメです。
本記事をおススメする人
- 材料力学を学び始めた方で、フックの法則が分からない人
- 高校物理で学んだフックの法則と材料力学のフックの法則の区別がつかない人
- 材料力学の予習でどんな感じかをつかみたい人
フックの法則で出てくる応力については下記の動画で解説していますので、参考にしていただければと思います。
フックの法則について
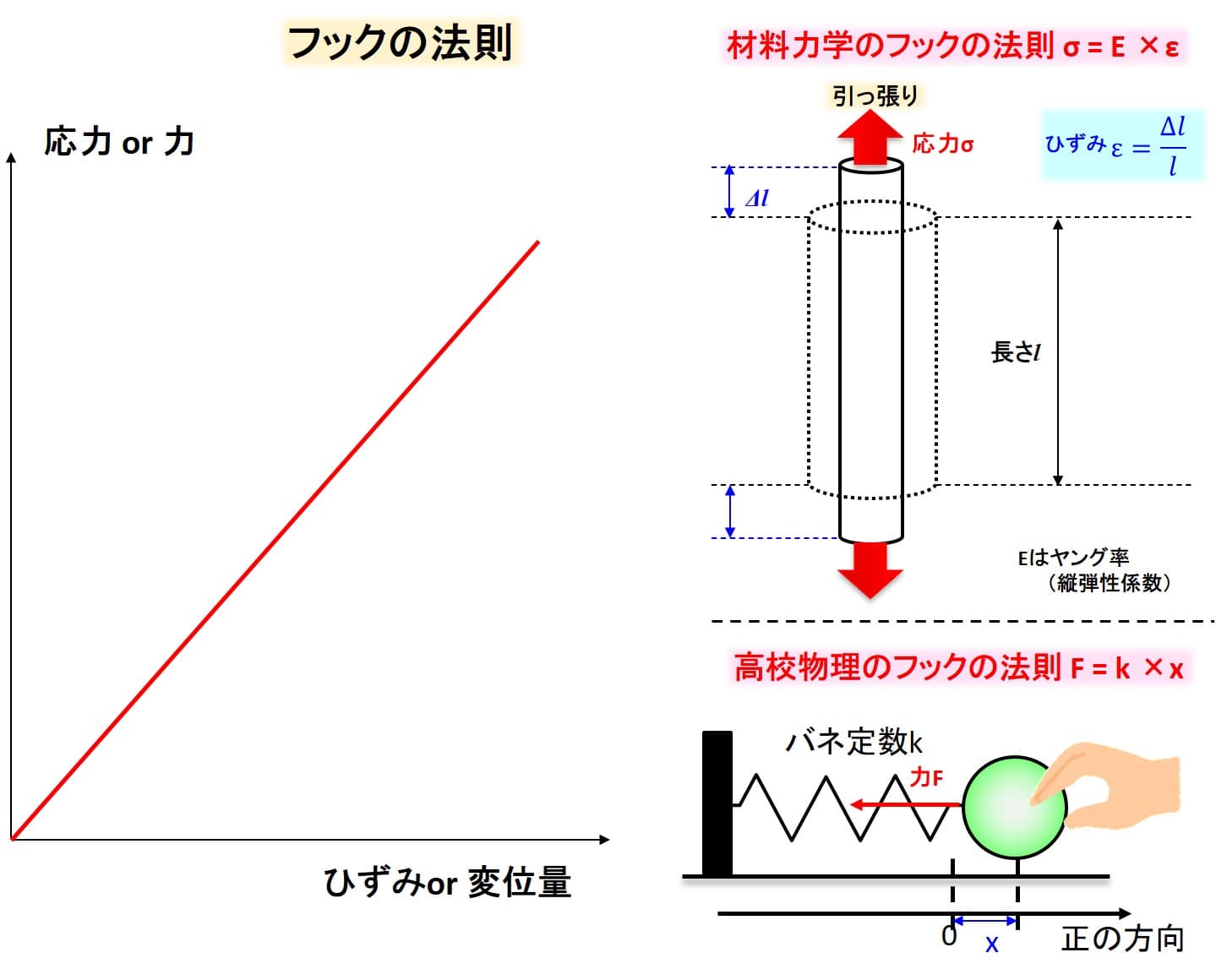
フックの法則は、 物体にかかった力に比例して変形する 、という経験則です。
高校物理では力と変位についての式で書かれていましたが、材料力学では、応力とひずみの関係式で表します。
表し方が違うだけで、本質的には同じことを指しています。
詳細を説明していきますね。
材料力学でのフックの法則
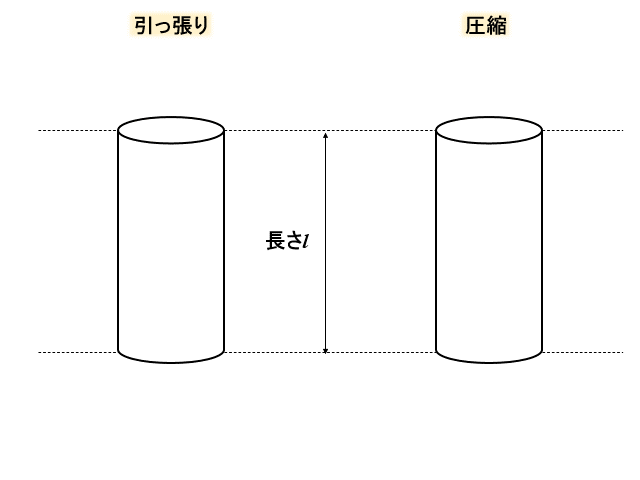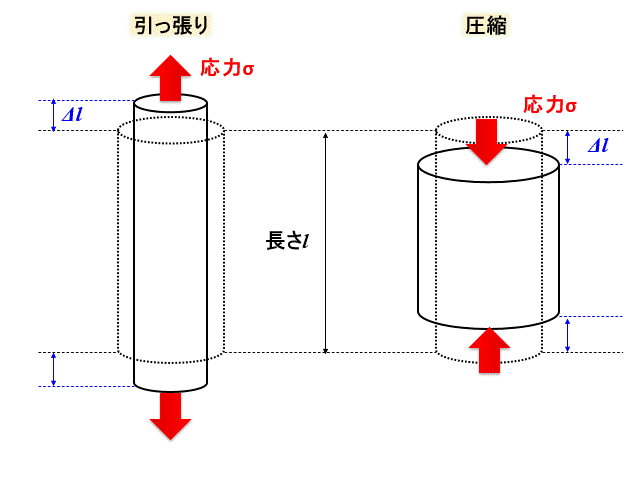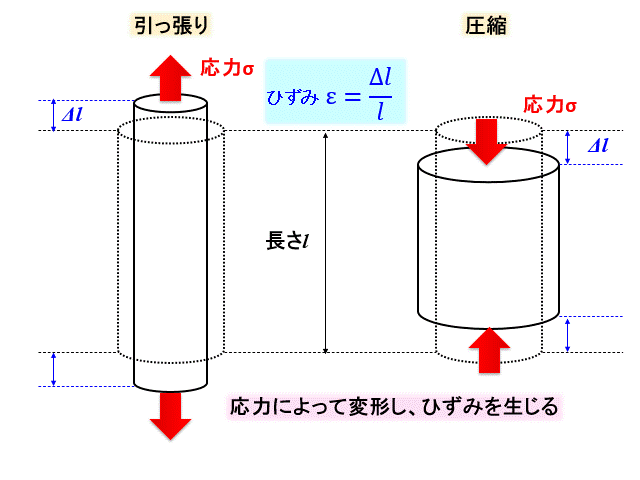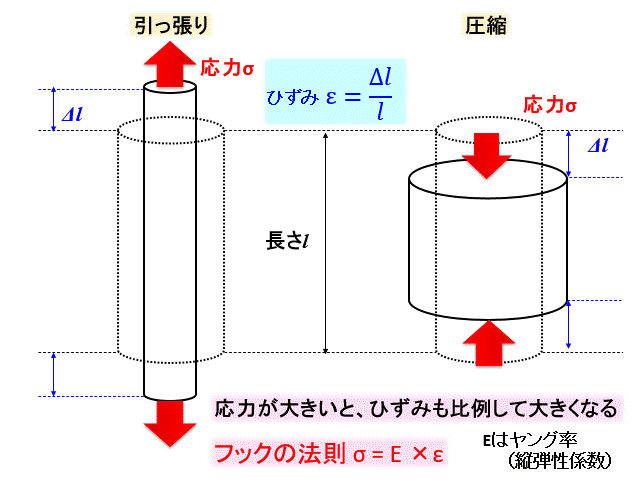
フックの法則は、引っ張り、圧縮の場合、応力を\(σ\)、ヤング率(縦弾性係数)を\(E\)、ひずみを\(ε\)とすると、
$$σ=Eε$$
となるような法則です。
" 応力は変形量に比例する"ということを示しています。
応力は単位面積あたりにかかる力で、ヤング率(縦弾性係数)は物体の材質の硬さを示す係数です。
詳細は過去記事で解説していますので、参考にしてください。
やっぱり高校で習ったフックの法則とちょっと違うような・・・


扱っている文字とかは違うね。高校で習ったフックの法則を見てみようか。
高校で習ったフックの法則
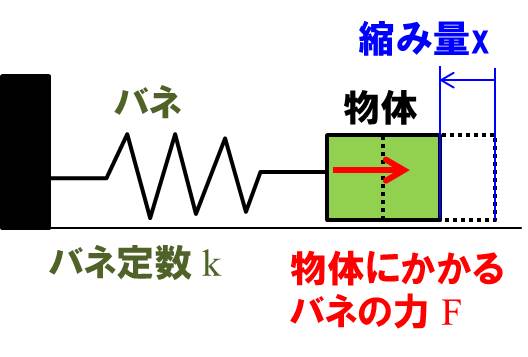
よく出てくるフックの法則は、上図のようにバネに物体がつながれている時、バネ定数を\(k\)、ばねの変位量を\(x\)、物体にかかる力を\(F\)とすると、
$$F=kx$$
こちらは" 物体にかかる力は変位量に比例する"ということを示しています。
高校物理でのフックの法則は過去の記事で解説していますので、参考にしてくださいね。
う~ん、力が変位量や変形量に比例している、というのは似ている気がするんだけど・・・


そうそう、違っている点を整理して、一つずつ理解していこうね。
材料力学のフックの法則と違う点
まず式を並べてみます。
材料力学:\(σ =E × ε\)
高校物理:\(F = k × x\)
材料力学の式では、左辺は応力、高校物理のフックの法則では力となっています。
単位
応力の単位は\(N/m^2\)、力の単位は\(N\)です。
ヤング率Eの単位は\(N/m^2\)、バネ定数は\)N/m\)です。
ひずみεは無次元、変位量\(x\)は\(m\)ですね。
単位は明らかに違いますね。
この単位の違いが何を表しているかですが、
高校物理では、1次元の方向にバネを引っ張ったときのケースを前提としており、
もっと一般的に表したものが材料力学のフックの法則である、ということです。
つまり、 材料力学で学ぶフックの法則の範囲の中に、高校物理のフックの法則がある 、というイメージですね。
まとめ
材料力学で学ぶフックの法則と、高校物理で学ぶフックの法則の違いについて解説しました。
これらは、 応力や力が、変形量に比例するという点で本質的には同じですが、
応力と力、ヤング率とバネ定数、ひずみと変位量と扱うパラメータが異なり、単位もそれぞれ異なっています。
この理由は 材料力学で学ぶフックの法則は、高校物理で学ぶフックの法則を、より一般的にしたものであることによるものでした。
それぞれの数式で出てくるパラメータの意味、単位をしっかり理解して、フックの法則を使いこなせるようにしましょうね。
初心者向けの参考書・教科書をこちらで紹介していますので、書籍選びに迷っている方は参考にしていただければと思います。
参考文献
- 現代材料力学:渋谷寿一、本間寛臣、斎藤憲司、朝倉書店
- 基礎材料力学[改訂版]:小泉堯(監修)、笠野英秋, 原利昭, 水口義久、養賢堂
- 材料力学 第3版:黒木剛司郎、森北出版株式会社
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
次の記事→材料力学 ひずみの種類とポアソン比