振動・波動の基礎-⑬2自由度の減衰強制振動の挙動について

2自由度の減衰ありって計算が複雑なんでしょ？もう計算しなくていいの？

苦手君

デルタ先生

かなり複雑な計算だから、毎回計算する必要は無いよ。でも一度、どのように解いていけばよいか、というのは理解しておいた方が、運動を理解しやすくなるから一度解いてみようか。

本記事では、2自由度の場合、減衰ありの状態で、強制振動の運動方程式を見てみましょう。

ちなみにこの2自由度のモデルは、動吸振器、あるいはダイナミックダンパーと呼ばれるものに相当します。

細かい計算は抜きですが、こういう風に解いていくんだ、という流れを見ておきましょう。

本記事をおススメする人

2自由度の振動について減衰がある場合を理解したい人
動吸振器、ダイナミックダンパーの勉強をしたい人
物理を勉強していて興味がある人、仕事で振動の知識を使う人

動画でも解説しておりますので、是非参考にしていただければと思います。

2自由度の減衰強制振動のモデル

まず、自由振動のモデルは下記にようになります。

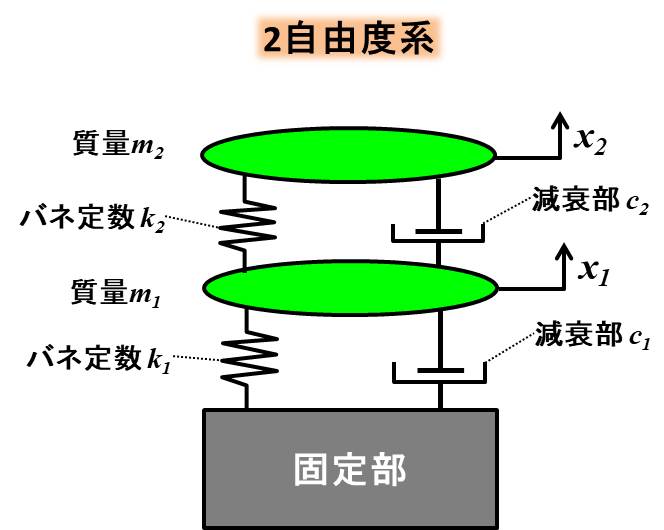
このモデルに強制振動を加えるわけですね。

質量$m_1$に周期的外力$f_1=Fcosωt$を付け加えましょう。

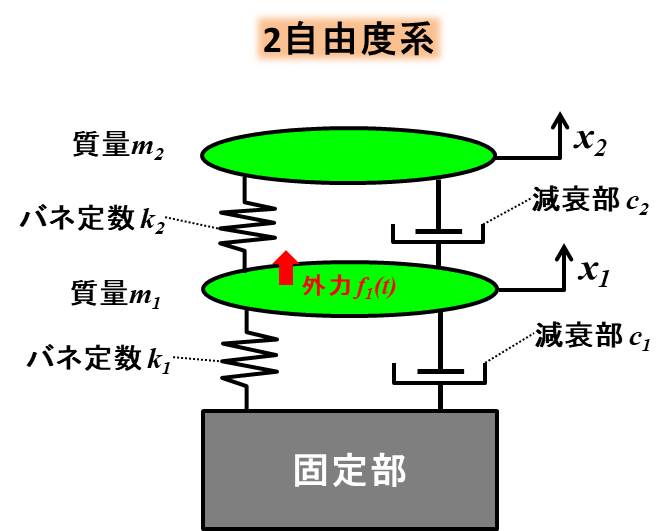
運動方程式は下記のようになりますね。

$$m_1\ddot{x_1}+(c_1+c_2)\dot{x_1}+(k_1+k_2)x_1-c_2\dot{x_2}-k_2x_2=Fcosωt・・・①$$

$$m_2\ddot{x_2}+c_2\dot{x_2}+k_2x_2-c_2\dot{x_1}-k_2x_1=0・・・②$$

連立の線形微分方程式ですね。

運動方程式を解く

さて、自由振動の場合、①の右辺がゼロになるので、簡単なはずなのですが、それでも計算が複雑になることを過去の記事で解説しました。

じゃあ、解けないじゃないか！という声が聞こえてきそうですが、

今回は、複素数を使用して、解いていきます。

複素数の解法については下記を参考にしてください。

参考記事

さて、複素数での解き方のおさらいですが、まず、複素数の特殊解を設定するのでしたね。

複素数の特殊解を考えるときに、大事な公式としてオイラーの公式があり、これを使います。

オイラーの公式

$$e^{iθ}=cosθ+isinθ$$

このオイラーの公式を見ていると、$cos$だけでなく$sin$の項がありますね。

ということで、$sin$の項を作りましょう。

$Fcosωt$という周期的外力が$m_1$に与えられていますが、$Fsinωt$の場合も考えてみましょう。

$cos$を$sin$にすると90°位相がずれるだけで、この場合の質量$m_1、m_2$の変位を$y_1、y_2$とします。

そうすると、運動方程式は下記のようになります。

$$m_1\ddot{y_1}+(c_1+c_2)\dot{y_1}+(k_1+k_2)y_1-c_2\dot{y_2}-k_2y_2=Fsinωt・・・③$$

$$m_2\ddot{y_2}+c_2\dot{y_2}+k_2y_2-c_2\dot{y_1}-k_2y_1=0・・・④$$

$x$が$y$に変わっただけですね。

$z_1=x_1+iy_1、z_2=x_2+iy_2$と複素数を設定して、①+i×③と②+i×④を計算してみると、

$$m_1\ddot{z_1}+(c_1+c_2)\dot{z_1}+(k_1+k_2)z_1-c_2\dot{z_2}-k_2z_2=F(cosωt+isinωt)・・・⑤$$

$$m_2\ddot{z_2}+c_2\dot{z_2}+k_2z_2-c_2\dot{z_1}-k_2z_1=0・・・⑥$$

⑤の右辺はオイラーの公式で、$F(cosωt+isinωt)=e^{iωt}$となりますね。

ここまで来て、特殊解を設定します。

$z_1=Z_1e^{iωt}、z_2=Z_2e^{iωt}$と特殊解を置くと、微分したものは、

$$\dot{z_1}=iωZ_1e^{iωt}、\dot{z_2}=iωZ_2e^{iωt}$$

$$\ddot{z_1}=-ω^2Z_1e^{iωt}、\ddot{z_2}=-ω^2Z_2e^{iωt}$$

となります。

これらを⑤、⑥に代入して、$e^{iωt}$を消去しましょう。

この連立方程式を行列で書きます。

$$\left(\begin{array}{cc}-ω^2m_1+iωc_1+iωc_2+k_1+k_2&-iωc_2-k_2\\-iωc_2-k_2&-ω^2m_2+iωc_2+k_2\end{array}\right)\left(\begin{array}{c}Z_1\\Z_2\end{array}\right)=\left(\begin{array}{c}F\\0\end{array}\right)・・・⑦$$

これを解きましょう。

行列を使って連立方程式を解く

$$\left(\begin{array}{cc}A&B\\C&D\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right)=\left(\begin{array}{c}F\\0\end{array}\right)$$

この連立方程式の解は、行列式$Δ=AD-BC$とすると、

$$x_1=\frac{D}{AD-BC}F=\frac{D}{Δ}F$$

$$x_2=\frac{-C}{AD-BC}F=\frac{-C}{Δ}F$$

連立方程式の行列式をΔと置くと、

$$Δ=det\left[\begin{array}{cc}-ω^2m_1+iωc_1+iωc_2+k_1+k_2&-iωc_2-k_2\\-iωc_2-k_2&-ω^2m_2+iωc_2+k_2\end{array}\right]$$

$Z_1$と$Z_2$を求めると、

$$Z_1=\frac{-ω^2m_2+iωc_2+k_2}{Δ}F・・・⑧$$

$$Z_2=\frac{iωc_2+k_2}{Δ}F・・・⑨$$

$Z_1、Z_2$は複素数なので、下記のように表せます。

$$Z_1=A_1+iB_1、Z_2=A_2+iB_2$$

特殊解$z_1、z_2$に代入すると、

$$z_1=Z_1e^{iωt}=(A_1+iB_1)(cosωt+isinωt)$$

$$z_2=Z_2e^{iωt}=(A_2+iB_2)(cosωt+isinωt)$$

実部と虚部に分けて書くと、

$$z_1=(A_1cosωt-B_1sinωt)+i(A_1sinωt+B_1cosωt)$$

$$z_2=(A_2cosωt-B_2sinωt)+i(A_2sinωt+B_2cosωt)$$

今回与えられた周期的な外力は、$Fcosωt$なので、変位$x_1、x_2$はこの複素数の実部に相当します。

$$x_1=A_1cosωt-B_1sinωt$$

$$x_2=A_2cosωt-B_2sinωt$$

三角関数の合成の公式から、

$$x_1=X_1cos(ωt-Φ_1)、x_2=X_2cos(ωt-Φ_2)$$

$$tanΦ_1=\frac{-B_1}{A_1}、tanΦ_2=\frac{-B_2}{A_2}$$

$$X_1=|Z_1|=\sqrt{A_1^2+B_1^2}、X_2=|Z_2|=\sqrt{A_2^2+B_2^2}$$

あれ？ここで終わり？？$A_1$とか未知数のまま？

苦手君

デルタ先生

ふつうはここまでの計算で、数値計算で大丈夫になることが多いよ。$A_1$などの未知数は$z$の振幅から求めることができるから、未知数ではないんだよ。

計算過程で勝手においた$A$や$B$ですが、これは計算すると求めることができます。

⑧式や⑨式から$Z_1$と$Z_2$について、複素数表記がされているので、これらを力業で実部と虚部に分けることで$A$と$B$の値を出すことができます。

計算が非常に面倒なので、余力のある人は解いてみてください。

$A$と$B$を求めた上で、振幅$X_1$と$X_2$がどのようになるか、結果を記しておくと、

$$X_1=\frac{\sqrt{(k_2-ω^2m_2)^2+(ωc_2)^2}}{\sqrt{a^2+b^2}}F$$

$$X_2=\frac{\sqrt{k_2^2+(ωc_2)^2}}{\sqrt{a^2+b^2}}F$$

$$Φ_1=tan^{-1}\frac{(-ω^2m_2+k_2)b-ωc_2a}{(-ω^2m_2+k_2)a+ωc_2b}$$

$$Φ_2=tan^{-1}\frac{-k_2b+ωc_2a}{-k_2b-ωc_2a}$$

$$a=(-ω^2m_1+k_1+k_2)(-ω^2m_2+k_2)-k_2^2-ω^2c_1c_2$$

$$b=ω[(-ω^2m_2+k_2)c_1+(-ω^2(m_1+m_2)+k_1)c_2]$$

$a$と$b$は行列式Δの実部と虚部となっています。

これで減衰強制振動の特殊解が求まりました。

特殊解の挙動

それでは、この特殊解の挙動を実際に見てみましょう。

質量、バネ定数、外力の振幅は全て1、減衰係数は0.1で計算したグラフが下記です。

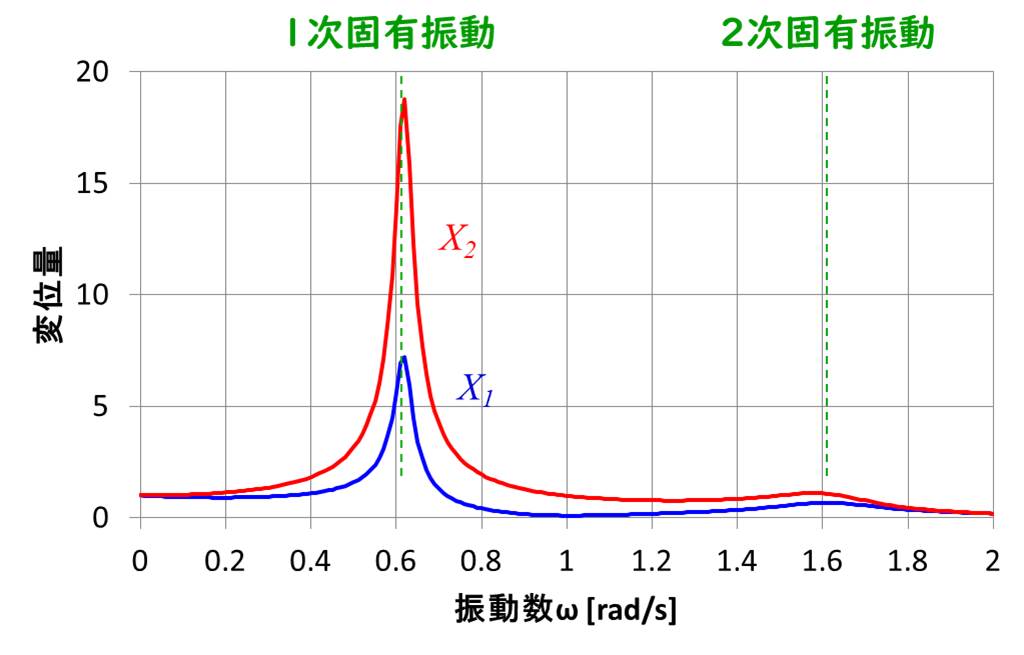
それぞれの固有振動モードで、有限の値をとり、さらに2次固有振動モードの振幅が非常に小さくなりました。

このモデルは、振動を抑える構造としてよく扱われ、動吸振器やダイナミックダンパーと呼びます。

1つの質点だと、共振したときの振動が大きくなってしまいますが、2つ目の質点を付加させることで、振動を抑えようというものです。

共振を抑えるために、どのような$m_2、k_2、c_2$を選択すればよいか、このモデルによって最適値が計算されるわけです。

まとめ

以上、2自由度の減衰強制振動について解説しました。

減衰が入ることで、共振したときの振幅が有限の値になる、ということは1自由度のときと変わりません。

このことを利用して、動吸振器やダイナミックダンパーの設計がなされます。

動吸振器の設計については、リンク先の記事で解説していますので、最後にご紹介させていただきます。

参考文献

振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
Wikipedia

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

本サイトの振動工学のページはこちら。

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎-⑭動吸振器の設計と定点理論のグラフ