2自由度の減衰ありで運動方程式を解けないんだけど…


減衰ありの状態で計算するのは、凄く難しくなってくるんだ。考え方はこれまでと同じでもいいんだけど、計算力が必須だね。
本記事では、2自由度の減衰自由振動について解説します。
注意事項ですが、過去記事のように、本記事では方程式を最後まで解いていません。
というか 手計算ではそうそう簡単に解けません。
ということを解説します。
本記事をおススメする人
- 2自由度の振動について減衰がある場合を理解したい人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
モデルと運動方程式
モデルは下記にようになります。
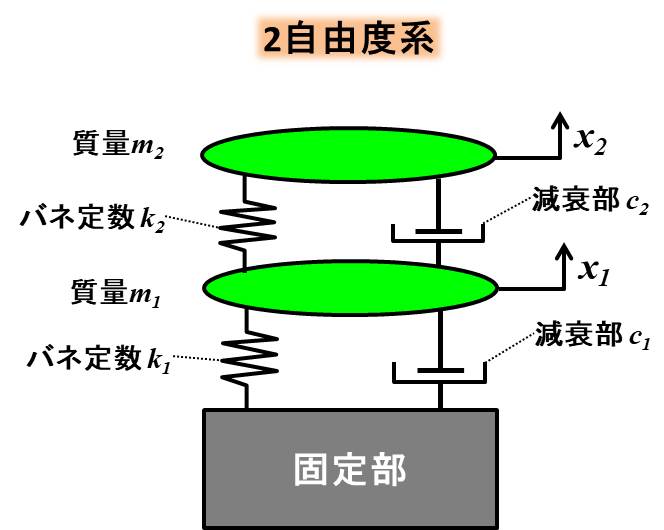
前回までは、減衰部分の\(c_1\)、\(c_2\)が無い非減衰の場合を考えていましたが、今回はこの減衰項が入った状態で考えます。
1自由度のときと同じく、速度に比例した減衰力が発生すると考えた場合、運動方程式は、下記のようになります。
連立の線形微分方程式ですね。
運動方程式を解く
さて、1自由度の減衰あり運動方程式の解き方は覚えていますでしょうか?
過去記事を参考にしてくださいね。
1回微分の項があるので、特殊解を三角関数ではなく、\(e\)の指数関数で置くのでしたね。
この解法を、2自由度の非減衰自由振動の解き方に応用してみましょう。
特殊解を\(x_1=A_1e^{λt}、x_2=A_2e^{λt}\)とすると、
\(\dot{x_1}=A_1λe^{λt}、\dot{x_2}=A_2λe^{λt}、\ddot{x_1}=A_1λ^2e^{λt}、\ddot{x_2}=A_2λ^2e^{λt}\)となりますので、
これらをすべて①、②式の運動方程式に代入しましょう。
①式は
\(e^{λt}\)を消去できるので、消去すると、
同様に②式は、
これも\(e^{λt}\)を消去して、
③と④を連立させ、行列で書くと、
ここから、\(A_1、A_2\)がともにゼロでないという、1次従属の条件から、λを求めます。
行列式=0となることが、その条件ですので、
整理すると、
$$(m_1λ^2+(c_1+c_2)λ+(k_1+k_2))(m_2λ^2+c_2λ+k_2)-(-c_2λ-k_2)(-c_2λ-k_2)=0$$
ん~?これって解けるの??


λの4次方程式になっているね。しかも$λ^3$の項も残るから、高度な数学を使わないと難しいんだ。
結論、解けないことはないけど、非常に計算が難しい、ということです。
実は、減衰がある2自由度の自由振動や強制振動について、詳細に解いた教科書も少ないのが現状です。
計算は複雑なので略、みたいな形で書いてある本が多いですね。
どのような挙動をするのか
これについては1自由度のときと同じで、 減衰があることによって、時間が経つと振幅はゼロに収束します。
自由振動成分はゼロに収束する、という事実さえ押さえておけば、強制振動を考えるときには、これまで通り特解にのみ注目すればOKになります。
初学者の方は、 減衰のある自由振動成分は、時間の経過でゼロに近づく、ということを頭に入れておきましょう。
まとめ
本記事では、 これまでの1自由度の解き方で2自由度の計算をすると、非常に煩雑な計算になることを示しました。
計算力のある人であれば、解くこともできるとは思いますが、現実問題、解く必要もないことも多いです。
減衰を入れることでどのような挙動になるか、を理解することの方が大事で、 自由振動成分は時間の経過でゼロに近づく、ということを理解しましょう。
減衰とは振動を邪魔するものなのですから、振動がどんどん無くなっていくわけです。
自由度が増えてもこれは変わりません。
複雑な計算部分ですが、需要があれば計算結果も記事にしようと思います。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 振動・波動:小形正男、裳華房
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎-⑬2自由度の減衰強制振動の挙動について