2自由度の強制振動が、動吸振器やダイナミックダンパーの設計に使われるって聞いたけど、実際はどのように設計するの?


それじゃあ、2自由度のモデルを使って、どのように設計したらいいか考えてみようか。
今回は、2自由度の強制減衰振動のモデルを使って、どのように振動を制御するかを解説します。
ましょう。
本記事をおススメする人
- 動吸振器、ダイナミックダンパーの設計の勉強をしたい人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
下記の動画で一部解説していますので、参考にしてください。
2自由度のモデル
まず、動吸振器のモデルですが、これまでの質量を\(m_1、m_2\)と呼んできました。
この記事では、土台に直接つながっている質量を 主系、主系につながっている質量を 従系と呼びます。

多くの教科書でもこのように主系、従系で読んでいますので、この表記で進めます。
主系に減衰が無い場合
まず、主系に減衰が無い場合を考えます。
このモデルは下記のように書けます。
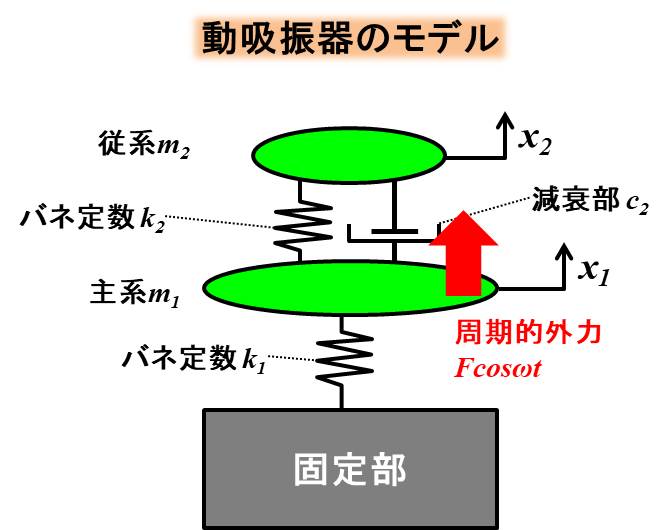
この運動方程式は、下記のようになります。
詳細の計算は過去の記事を参考にしてください。
2自由度で、減衰が2個ついている運動方程式を、上記の過去記事で解説しております。
このモデルから\(c_1\)を除いた式になります。
減衰のある2自由度の強制振動の変位は、下記のようになります(これも過去記事を参照)。
応答倍率について
さて、ここで、 応答倍率という概念を導入します。
応答倍率とは、強制振動の状態において、 振動の振幅と同じ静荷重を与えた場合の変位に対し、何倍の振幅になるか、を示したものになります。
強制振動を\(Fcosω\)とすると、静荷重Fを与えた時の変位に対して、どれくらい変位するか、ですので、
静荷重を与えた時の変位を\(X_{st}\)とすると、フックの法則から、
$$F=kX_{st}→X_{st}=\frac{F}{k}$$
強制振動のときの変位を\(X_d\)、応答倍率\(M_d\)は、
$$M_d=\frac{X_d}{X_{st}}$$
となります。
この応答倍率で考えると、式がすっきりして見やすくなることと、無次元化されることで、どんな振幅の加振に対しても成り立つ、という便利さがあります。
で、この応答倍率で考えるのですが、\(m\)とか\(k\)とか\(c\)とか、いろいろ変数変換します。
- 主系と従系の質量の比:\(μ=\frac{m_2}{m_1}\)
- 主系の固有振動数:\(Ω_1=\sqrt{\frac{k_1}{m_1}}\)
- 従系の固有振動数:\(Ω_2=\sqrt{\frac{k_2}{m_2}}\)
- 主系と従系の固有振動数の比:\(κ=\frac{Ω_2}{Ω_1}\)
- 減衰比:\(ζ=\frac{c_2}{2m_2Ω_1}\)
- 外力の振動数と主系の固有振動数の比:\(γ=\frac{ω}{Ω_1}\)
新しい変数がいっぱい出てきて大変ですが、こういう風に変数をおいたらうまくいくんだ、と思ってください。
それぞれは数値解析するときに使うくらいです。
これらを使うと、主系の応答倍率は下記のようになります。
これも、こうなるんだ、で大丈夫です。
定点理論
大事なことは求めた式から、 どのように設計したらよいか、を考えることです。
それでは、まず、減衰比ζを変化させたグラフを見てみましょう。
例によって、簡単のため、質量、バネ定数、外力は全て1として計算しています。
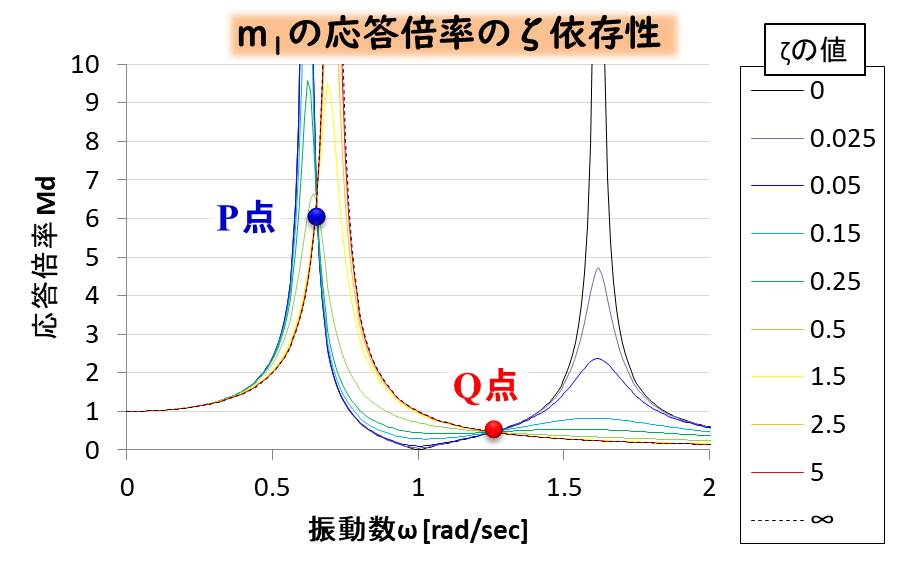
P点、Q点というものを設定しましたが、この点は どんなζでも通っていることがわかりますね。
質量比μと振動数比κを決めると、どんなζでもP点Q点を通る、これは 定点理論と呼ばれます。
ζが小さいとき
次にζが小さいときを見てみましょう。
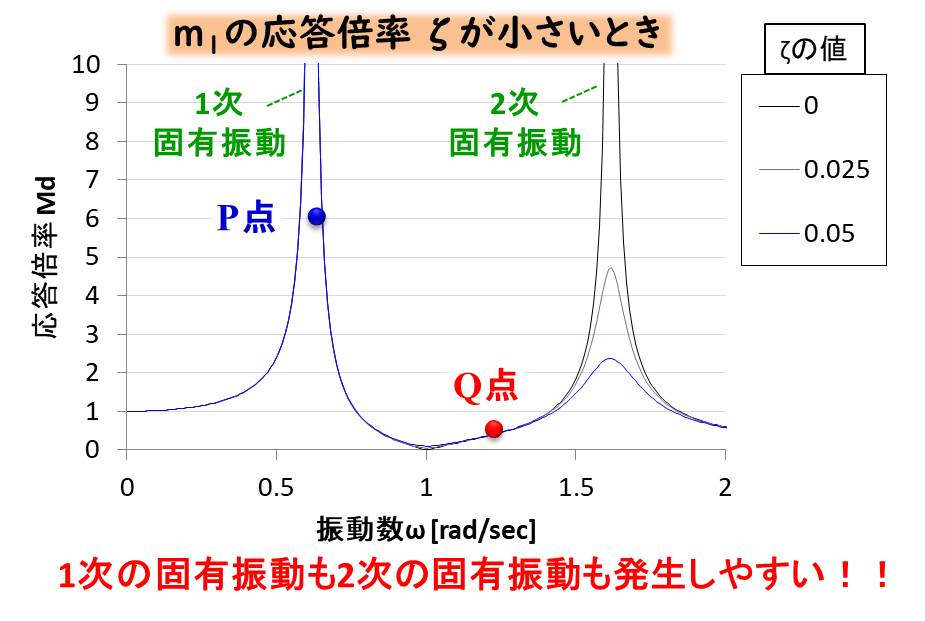
1次の固有振動のピーク(\(ω≒0.6\))と、2次の固有振動のピーク(\(ω≒1.6\))が大きくなっています。
これは、動吸振器の減衰が小さいと、1次の固有振動の周波数でも、2次の固有振動の周波数でも共振してしまう、ということです。
つまり、 共振を抑えたいのであれば、ある程度の減衰は必要ということですね。
そりゃそうです、ダンパーなんだからダンピング(減衰)がないと意味がないです。
ζが大きいとき
では、ζが大きければ大きいほど良いのか?という話になりそうですが、そうはいきません。
下のζが大きいときのグラフを見てみましょう。
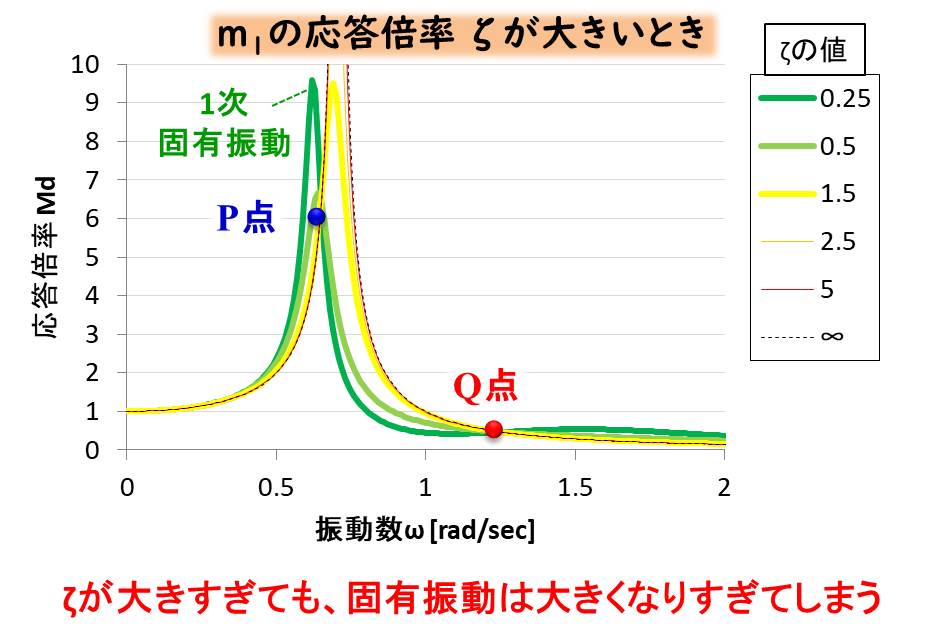
2次の固有振動モードはほとんど無くなるものの、1次の固有振動のピークはしっかり残っています。
薄い緑の\(ζ=0.5\)までは、1次の固有振動のピークは小さくなっていきます。
しかし、薄い緑の\(ζ=0.5\)よりも、黄色の\(ζ=1.5\)などは、\(ζ\)が大きいのにも関わらず、ピークが大きくなってしまっています。
減衰が大きいと、主系と従系が一緒に振動してしまい、1自由度系と同じ振る舞いとなり、1次の固有振動の周波数で 共振してしまうのです。
結論:振動を抑制したいのであれば、最適なζ(動吸振器の減衰\(c_2\))を選ぶこと!
κとμの依存性
最適っていうけど、具体的にはどんなζにしたらいいの?


最適なζの値は、κとμの値も考えた上で決めていかないといけないんだ。
定点理論とκ
では\(m_1\)の変位のκ依存性を見てみましょう。
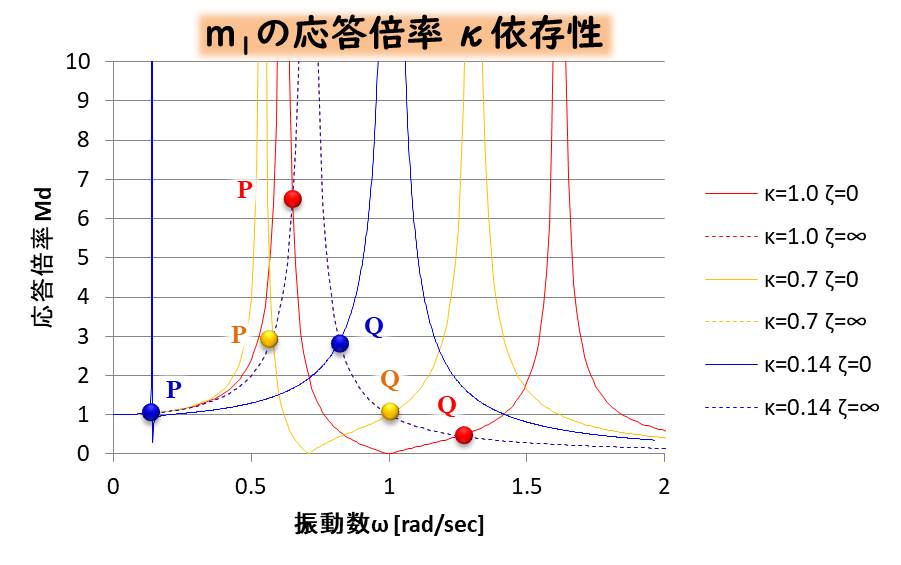
ζが∞のライン(グラフの点線)が、すべてのκで同じになっていますね。
一方で、ζが0のとき、κが変化すると、周波数応答は変化しますので、P点もQ点も変化します。
κが増加するとPは大きく、Qは小さくなります。
物理的に考えると、κが大きいということは、\(Ω_2\)が\(Ω_1\)より大きくなる、ということですので、
主系に、硬いバネでつながれているダンパー、あるいは軽いダンパーをつけると、κが大きくなります。
硬いバネ、あるいは軽いダンパーだと、主系が1次固有振動で振動しても、従系のダンパーの振動数が違いすぎて、振動をうまく吸収してくれないイメージですね。
定点理論とμ
最後にμの依存性を見てみましょう。
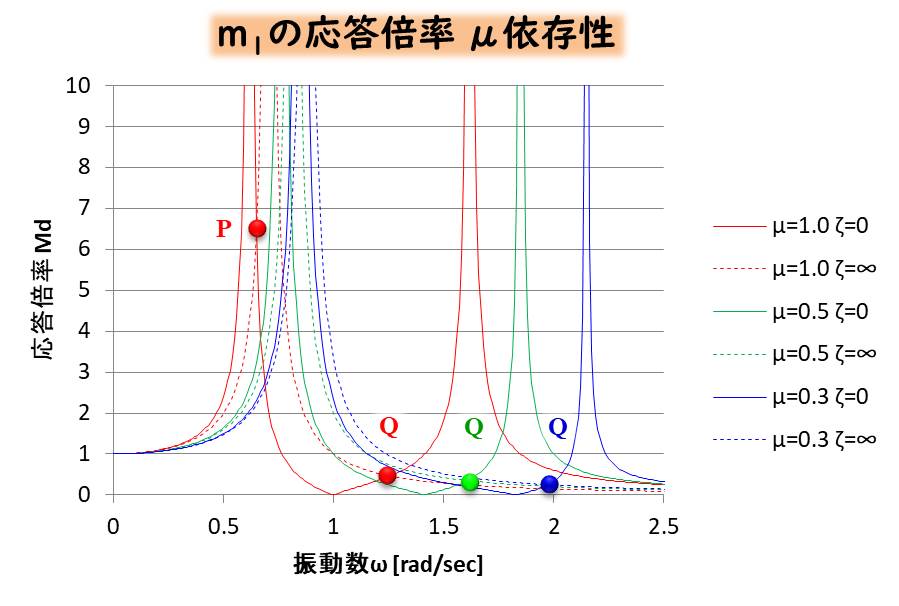
こちらは、ζが∞でも0でも、周波数応答が変化していることがわかりますね。
当然、P点もQ点もμによって変化します。
(μ=0.5、0.3のときのP点が10を超えてしまっていますが・・・グラフの上で変化しています)
ここまでのまとめ
動吸振器を付けた場合の主系の変位について見てきました。
ζが変化しても、定点理論からP点とQ点は変化しませんが、κ、μを変化させると、P点、Q点が動きます。
あとは、どのような周波数特性にしたいか、によって、これら3つのパラメータを選択すればよいわけです。
よくある設計として、μが決まっていて、すべての振動数において、できるだけ主系の振幅を減らしたい場合、を考えてみましょう。
動吸振器の設計の例
証明は省きますが、この場合のκとζを\(κ_{opt}、ζ_{opt}\)、応答倍率の最大値を\(M_{d max}\)とすると、それぞれ、
$$κ_{opt}=\frac{1}{1+μ}$$
$$ζ_{opt}=\frac{1}{2(1+μ)}\sqrt{\frac{3μ}{2(1+μ)}}$$
$$M_{d max}=\sqrt{\frac{2+μ}{μ}}$$
この場合のグラフを書きますと、下記のようになります。
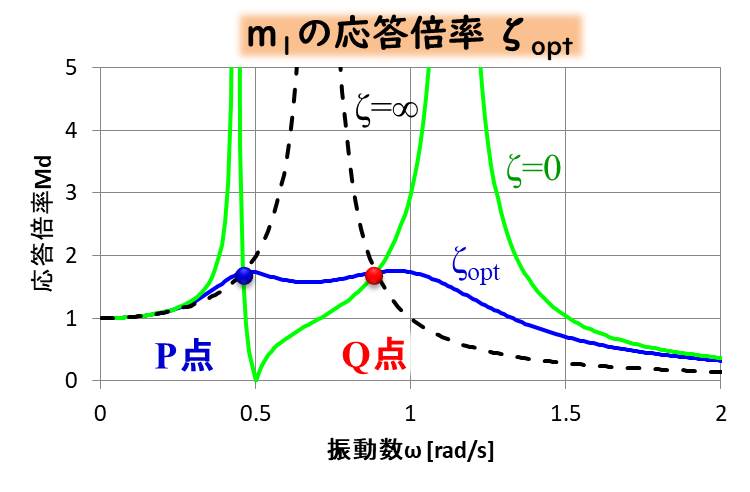
1次、2次の固有振動数である程度の共振が発生してしまいますが、かなりつぶれた波形になっています。
主系の振動をこのように抑制するものが、動吸振器、です。
まとめ
以上、動吸振器について解説しました。
動吸振器をつける質量を主系、動吸振器を従系とモデルでは呼びます。
また、静荷重の変位に対する、振幅の大きさを応答倍率\(M_d\)と呼び、どんな振幅の振動に対しても議論することができます。
動吸振器の減衰に関するζ、主系と従系の固有振動数の比をκ、主系と従系の質量の比をμとして、
これら3つのパラメータで動吸振器を設計します。
設計する際に重要な理論が、定点理論であり、ζが変化してもP点、Q点という2点は必ず通るという理論です。
このことを利用して、ζ、κ、μを設定し、必要な周波数応答の波形を作っていきます。
一例として、μが与えられた場合、動吸振器で\(M_{d max}\)を極小値にする設計と、その式を紹介しました。
少し、盛りだくさんでしたが、設計するときは、式の中に値を入れて、どのような周波数応答になるかを見ることになりますので、
どのようにパラメータを変化させていけばよいかをイメージできるように、グラフを頭に入れておきましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- Wikipedia
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら