-

-
後悔!ブログで数式を引用する際の注意点3点-計算ミスについて
2022/10/10 Word Press
筆者は苦しみました。 2020年6月中旬~7月中旬は、ほぼ毎日1記事のペースで記事を更新してきましたが、ここで急ブレーキ。 それは計算ミスによって、記事執筆を中断せざるを得ない状況に陥ったからです。 ...
-
-
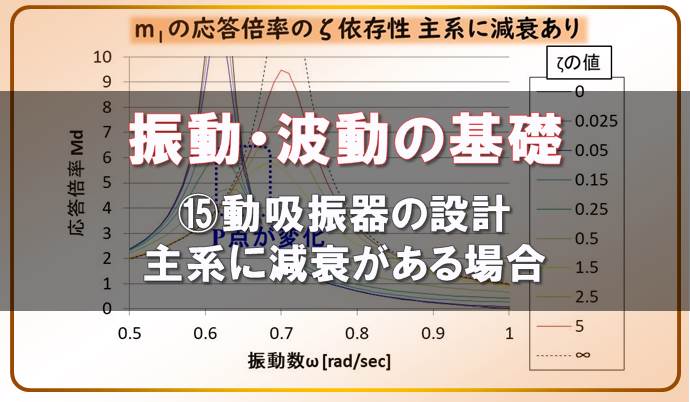
振動・波動の基礎-⑮動吸振器の設計 主系に減衰がある場合をグラフで確認する
今回は、動吸振器の主系に減衰がある場合を考えてみましょう。 本来ならば、数値解析を行う必要がありますが、今回は基礎的な内容から大きく外れてしまいますので、 グラフを確認し、定点理論から外れてしまうこと ...
-
-
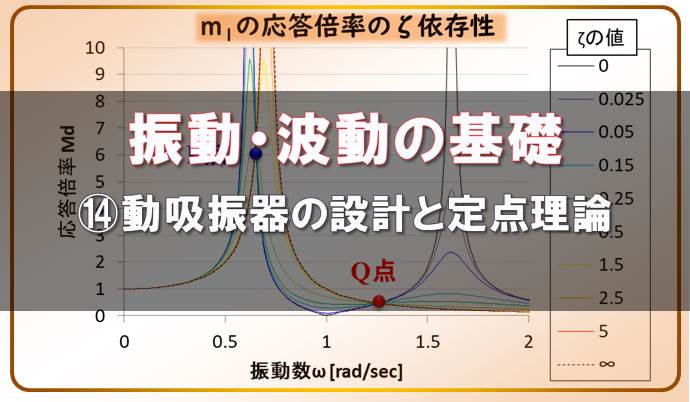
振動・波動の基礎-⑭動吸振器の設計と定点理論のグラフ
今回は、2自由度の強制減衰振動のモデルを使って、どのように振動を制御するかを解説します。 ましょう。 下記の動画で一部解説していますので、参考にしてください。 2自由度のモデル まず、動吸振器のモデル ...
-
-
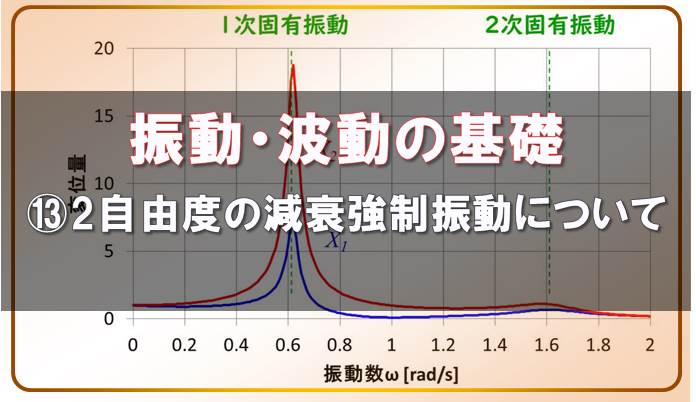
振動・波動の基礎-⑬2自由度の減衰強制振動の挙動について
本記事では、2自由度の場合、減衰ありの状態で、強制振動の運動方程式を見てみましょう。 ちなみにこの2自由度のモデルは、動吸振器、あるいはダイナミックダンパーと呼ばれるものに相当します。 細かい計算は抜 ...
-
-
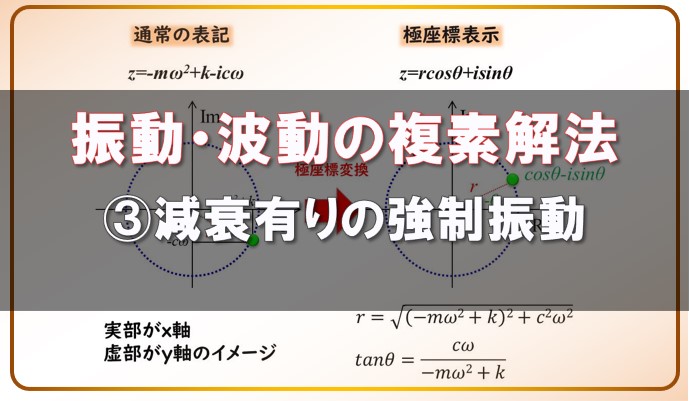
振動・波動の複素解法 ③減衰ありの強制振動の運動方程式
本記事では複素数を使った、減衰のある強制振動の解法について説明します。 前回、単振動の運動方程式について、複素数を使って解説しました。 複素数を使うことで、計算量がグっと減ることを示していきますね。 ...
-
-
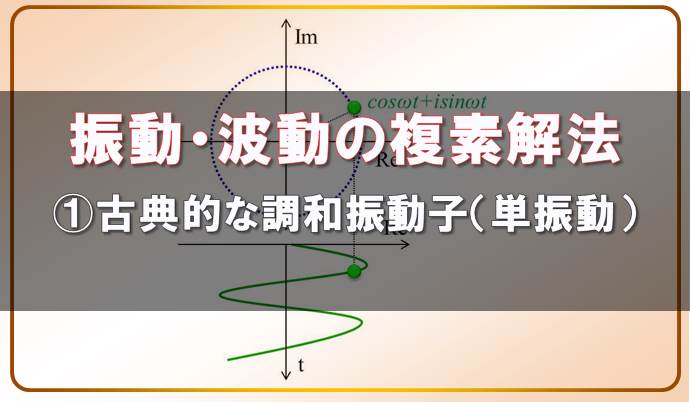
振動・波動の複素解法 ①古典的な調和振動子の運動方程式
本記事では複素数を使った、運動方程式の解法について説明します。 まずは一番簡単な調和振動子で、その扱い方に慣れていきましょう。 そもそも調和振動や単振動って何?という方は過去の記事を参考にしてください ...
-

-
50記事を3か月!使用しているツール10選
2022/10/10
2020年7月7日、50記事目を投稿しました! 3日坊主の私が、なんと3か月もブログを書き続けることができたことに、自分でも驚きです。。。 未だにアドセンスはコロナで通らず、アフィリも本気でやっていな ...
-
-
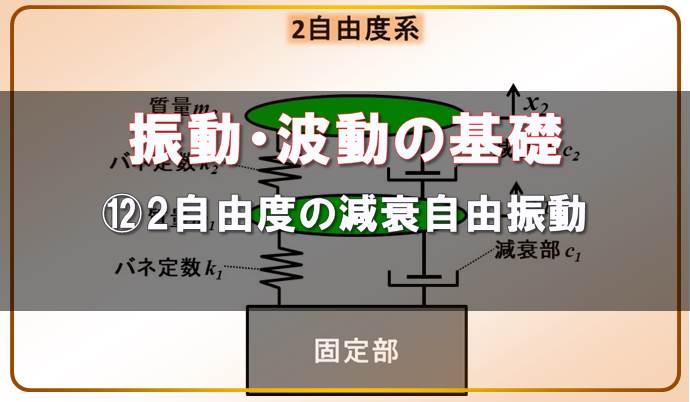
振動・波動の基礎-⑫2自由度系の減衰自由振動について
本記事では、2自由度の減衰自由振動について解説します。 注意事項ですが、過去記事のように、本記事では方程式を最後まで解いていません。 というか 手計算ではそうそう簡単に解けません。 ということを解説し ...
-
-
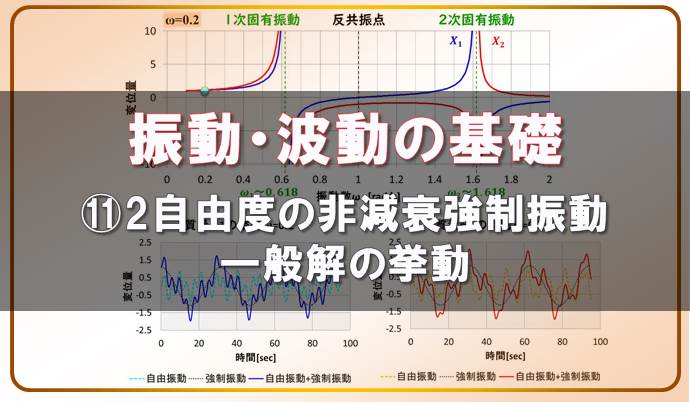
振動・波動の基礎-⑪2自由度系の非減衰強制振動の一般解
本記事では、2自由度の非減衰の強制振動の一般解の波形について解説します。 前回は強制振動の特解を求めて、その波形について解説しました。 今回はさらにリアルな振動として、一般解がどのようになっているのか ...
-
-
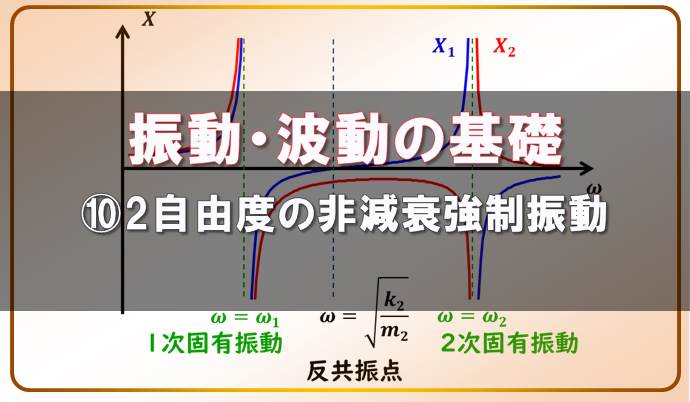
振動・波動の基礎-⑩2自由度系の非減衰強制振動と反共振点
本記事では、2自由度の非減衰の強制振動について解説します。 前回までで、2自由度の自由振動について解説しましたが、自由振動に周期的な外力が発生した場合にどのような動きをするか、イメージできるようになり ...
