大学物理 振動工学

振動・波動の基礎-⑮動吸振器の設計 主系に減衰がある場合をグラフで確認する

Google ad

動吸振器の設計をするときに、主系の減衰を0にしたけど、0じゃないときってどうなるの？

苦手君
デルタ先生

実際は主系にも減衰があるから、実際に近いモデルになるね。でも定点理論が成立しなくなったりして、非常に複雑になるんだ。

今回は、動吸振器の主系に減衰がある場合を考えてみましょう。

本来ならば、数値解析を行う必要がありますが、今回は基礎的な内容から大きく外れてしまいますので、

グラフを確認し、定点理論から外れてしまうことを確認しましょう。

前回、動吸振器で主系に減衰が無い場合を解説していますので、こちらも参考にしてください。

本記事をおススメする人

  • 動吸振器、ダイナミックダンパーの設計の勉強をしたい人
  • 物理を勉強していて興味がある人、仕事で振動の知識を使う人

動吸振器のモデル

今回、取り扱うモデルは下記です。

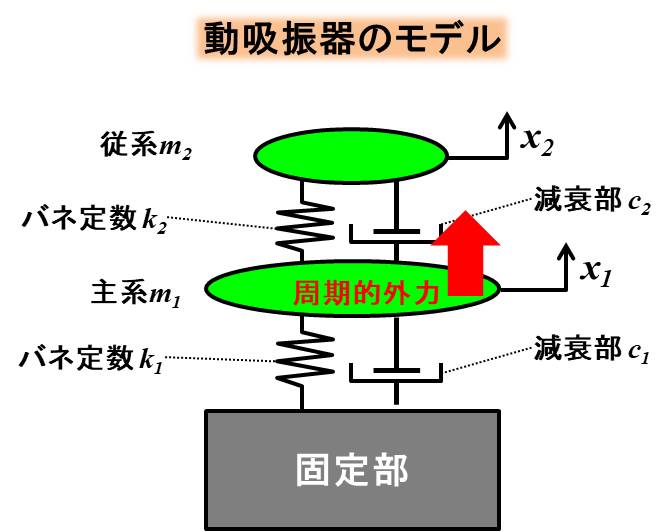
土台に直接つながっている質量を主系、主系に繋がっているもう一つの質量を従系と呼びます。

前回は主系に減衰が無い場合でしたが、今回は主系に減衰を付けた場合、どうなるかについて解説します。

運動方程式

運動方程式は、下記のようになります。

$$m_1\ddot{x_1}+(c_1+c_2)\dot{x_1}+(k_1+k_2)x_1-c_2\dot{x_2}-k_2x_2=Fcosωt・・・①$$
$$m_2\ddot{x_2}+c_2\dot{x_2}+k_2x_2-c_2\dot{x_1}-k_2x_1=0・・・②$$

減衰ありの動吸振器のモデルについてですが、実は過去に全く同じケースを取り扱っています。

[box class="blue_box" title="参考記事"]

振動・波動の基礎⑬-2自由度の減衰強制振動について

[/box]

複素数を用いて、特殊解を力業で計算していますので、計算の詳細が気になる方は参考にしてください。

特殊解の振幅は下記のようになるのでした。

$$X_1=\frac{\sqrt{(k_2-ω^2m_2)^2+(ωc_2)^2}}{\sqrt{a^2+b^2}}F$$
$$X_2=\frac{\sqrt{k_2^2+(ωc_2)^2}}{\sqrt{a^2+b^2}}F$$
$$Φ_1=tan^{-1}\frac{(-ω^2m_2+k_2)b-ωc_2a}{(-ω^2m_2+k_2)a+ωc_2b}$$
$$Φ_2=tan^{-1}\frac{-k_2b+ωc_2a}{-k_2b-ωc_2a}$$
$$a=(-ω^2m_1+k_1+k_2)(-ω^2m_2+k_2)-k_2^2-ω^2c_1c_2$$
$$b=ω[(-ω^2m_2+k_2)c_1+(-ω^2(m_1+m_2)+k_1)c_2]$$

現象を理解する上では、こういう振幅になるんだ、というくらいで大丈夫です。

主系に減衰がある場合の定点理論

結論的には、定点理論が使えなくなります。

つまり、最適な設計値は、明確な式で表すことができない、です。

実際にグラフを比較してみましょう。

例によって、計算を簡単にするために、主系、従系の質量とバネ定数、外力は1としています。

\(ζ=\frac{c_2}{2m_2Ω_1}、Ω_1=\sqrt{\frac{k_1}{m_1}}\)と、減衰比をおきます。

こちらは、主系に減衰が無い場合の\(ζ\)を変更したときのグラフです。

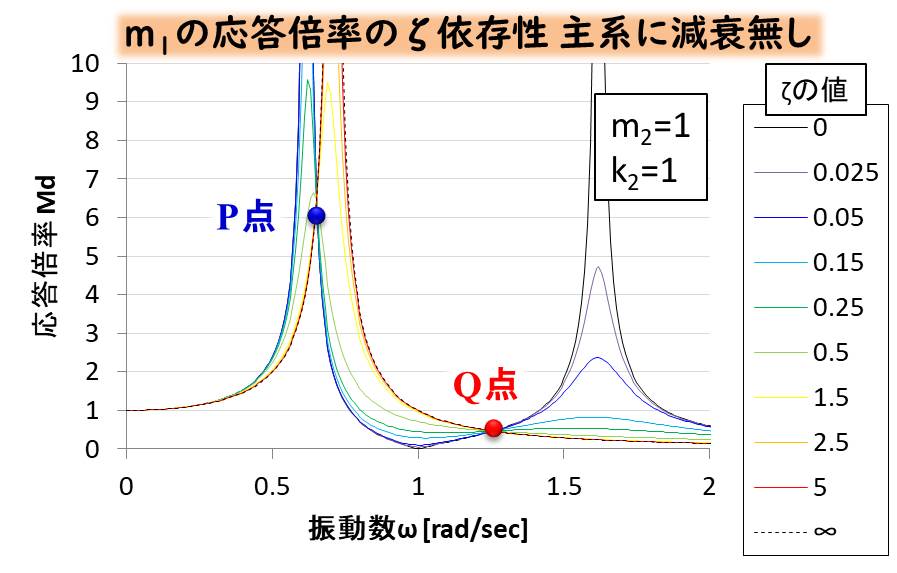
視覚的に理解するために、このグラフのP点とQ点の近くを拡大してみましょう。

まずはP点の近くを拡大してみます。

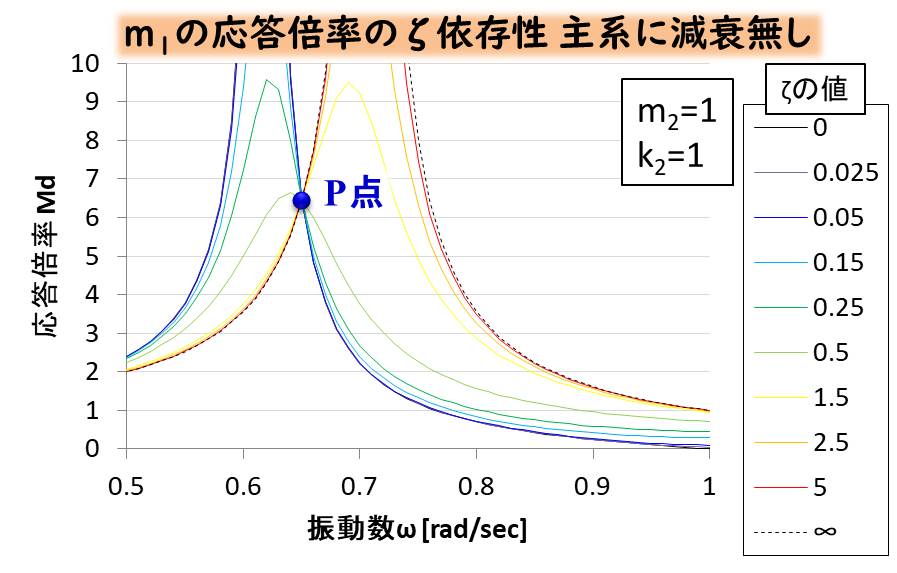
P点はどのζの値でも一定の場所にとどまっていますね。

次はQ点です。

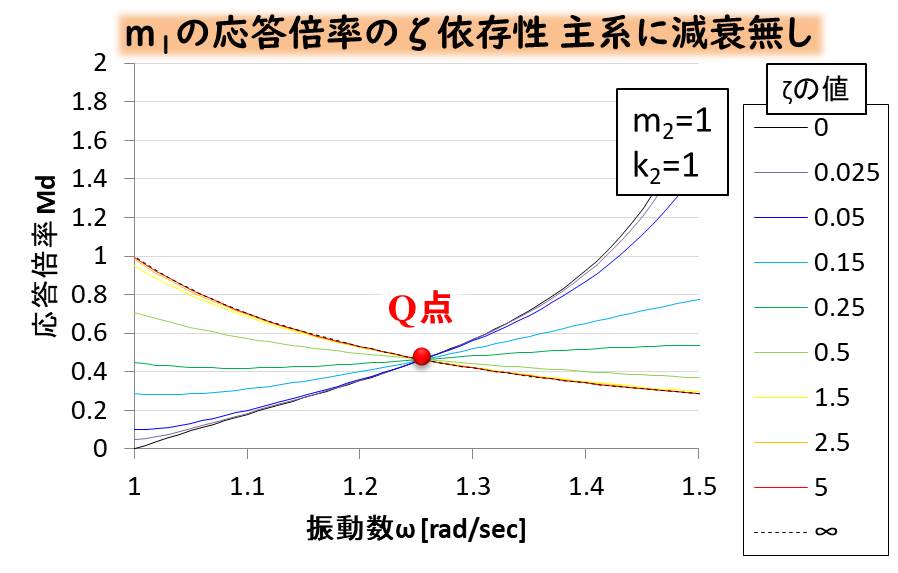
こちらも定点理論が成立しており、P点とQ点はζによって変化しません。

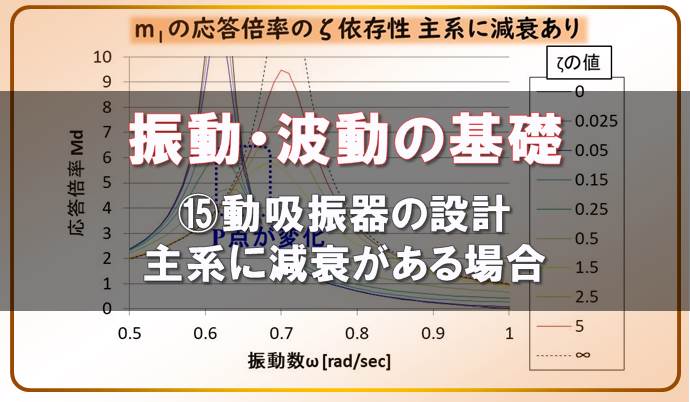
では主系に減衰がある場合を見てみましょう。

こちらは、減衰項がふたつあるので、\(ζ_2=\frac{c_2}{2\sqrt{m_2k_2}}\)と、従系の減衰比を設定します。

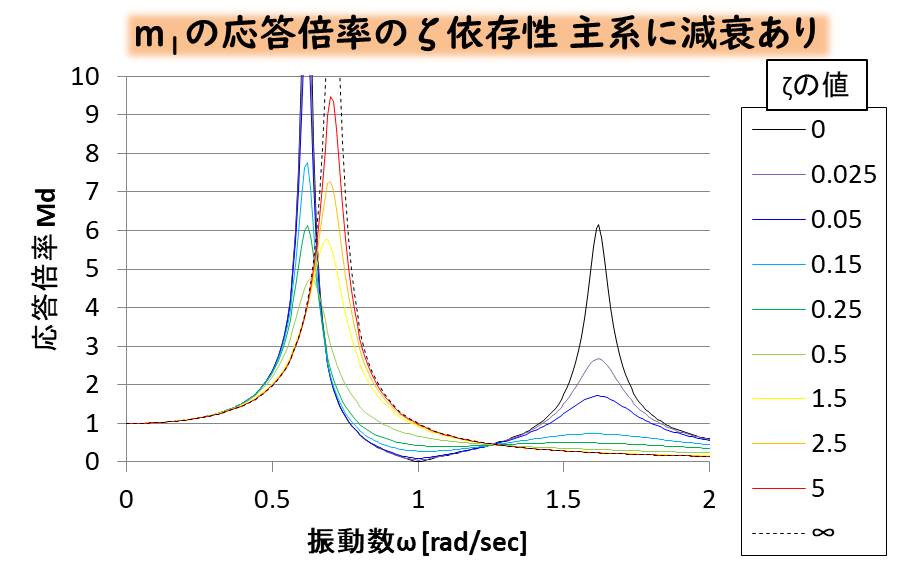
少しわかりにくいと思いますので、P点とQ点に相当する箇所を拡大してみましょう。

まずはP点です。

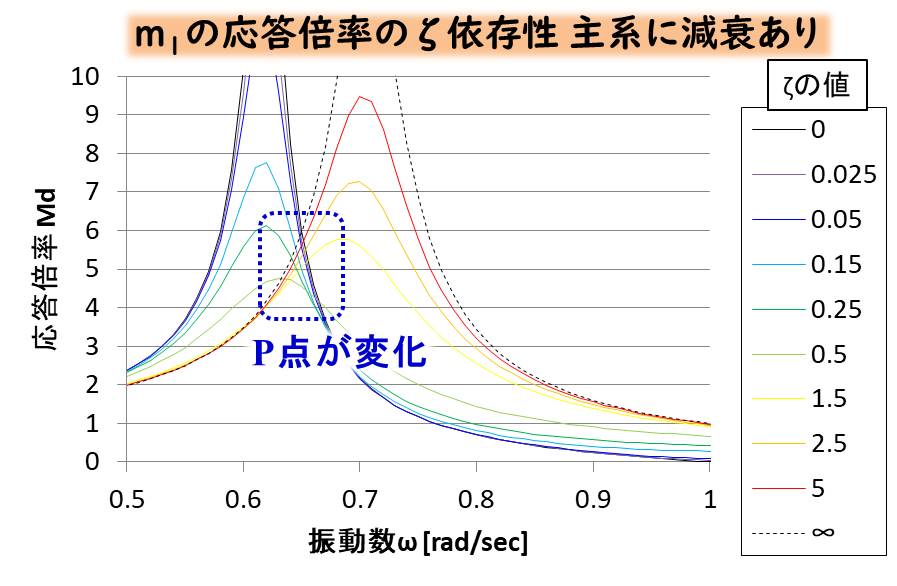
P点が動いていることが分かります。

このように主系に減衰が存在することで、定点理論が破綻してしまうのです。

ちなみにQ点も動いているのですが、このケースだと非常に微妙な動きになっています。

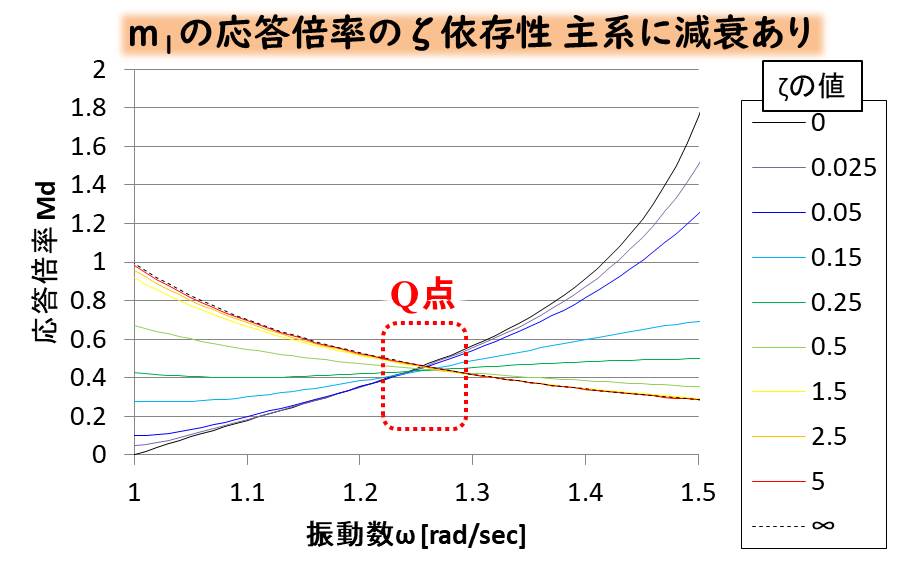
うん、わかりにくい・・・

Q点が動くような、もう少しわかりやすいケースを考えてみましょう。

従系の質量を0.5、従系のバネ定数\(k_2\)を0.3としたとき、グラフは下記のようになります。

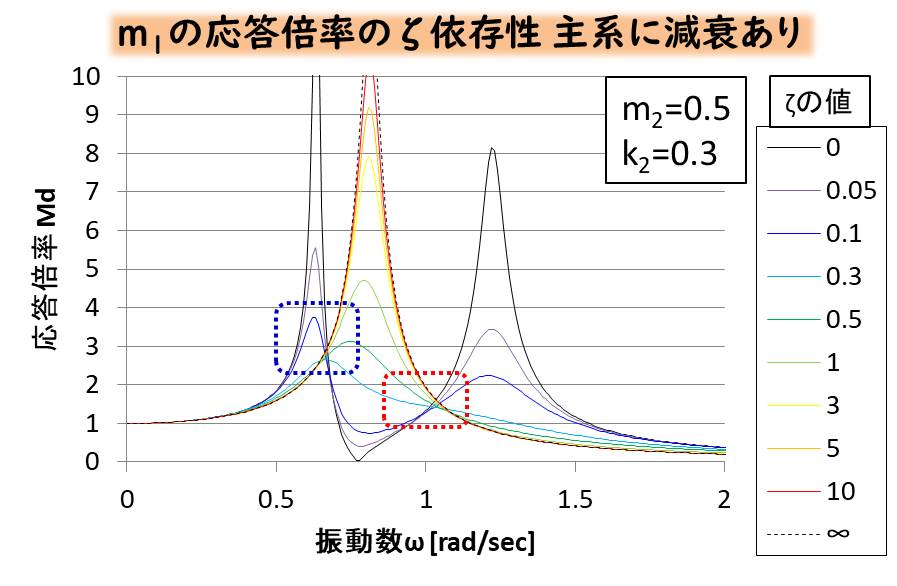
こちらのP点とQ点の近くを拡大したグラフは下記です。

まずはP点の近くを拡大したグラフです。

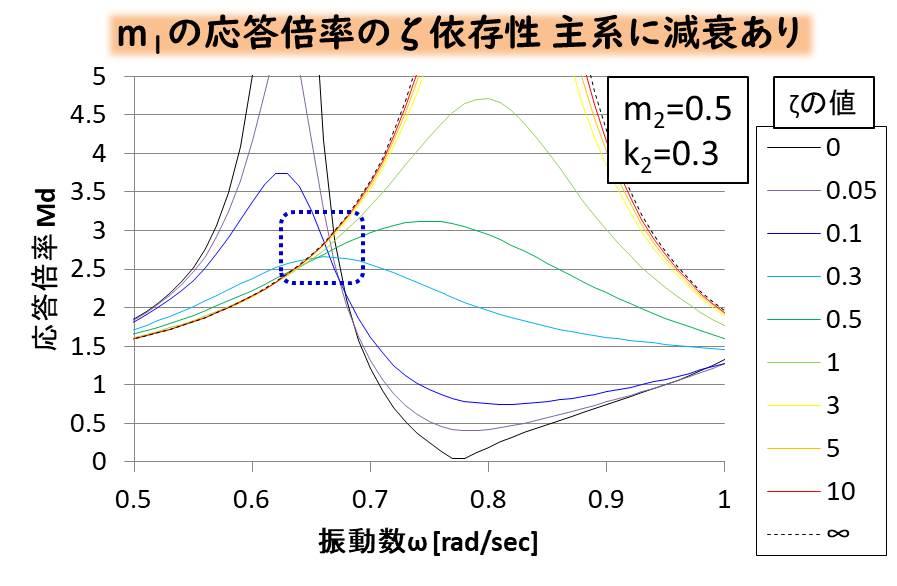
P点はこのケースでもしっかり動いていますね。

そして次はQ点。

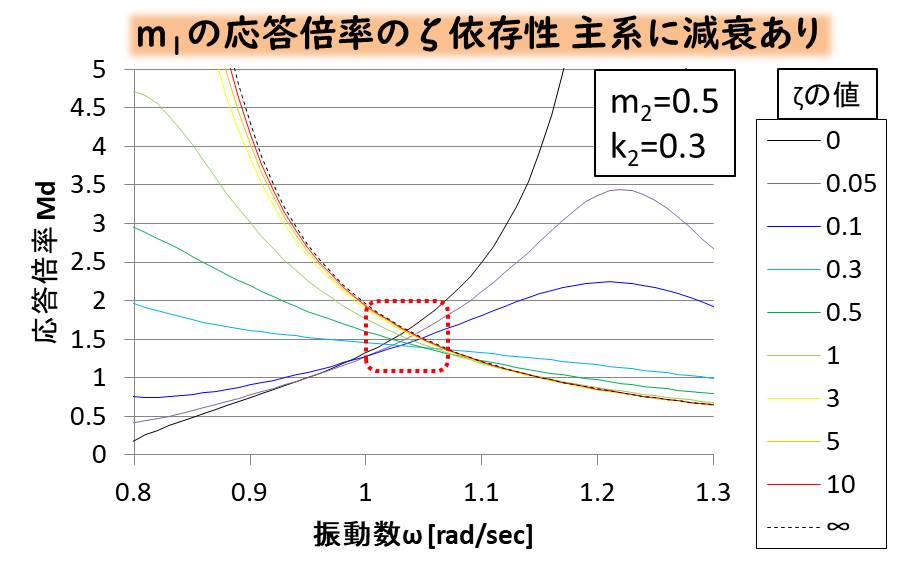
先ほど示した従系の質量が1、バネ定数が1のときと比べて、Q点の変動が大きくなっていることがわかりますね。

具体的に最適解を求める方法ですが、数値解析を行うか、近似式を使って求める、となります。

近似式については、こちらに示されていますので、参考にしていただければと思います。

まとめ

本記事では、主系に減衰項を入れると、定点理論が成立しなくなる、ということを解説しました。

最適解を近似的に求める方法も存在しますが、制限があったり、かなり複雑な式となります。

これ以上の詳細は基礎的な内容から大きく外れることになりますので、今回は割愛させていただきました。

初心者の方は、主系の減衰項のために定点理論が成り立たなくなる、ということをまずは頭に入れておきましょう。

参考文献

  • 主系の減衰を考慮した動吸振器の設計式について：第2報、定点理論に基づく設計法：浅見敏彦、細川[ヨシ]延、『日本機械学会論文集C編』第61巻第583号、1995年3月25日、 915-921頁
  • 振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
  • 機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
  • Wikipedia

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

本サイトの振動工学のページはこちら。

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎-⑯2自由度の連成振動（減衰無し、質量とバネ定数が同じ場合）

-大学物理, 振動工学
-, ,