材料力学をやることになったんだけど、どういう知識が必要になるの?


それじゃあ今日は材料力学を学ぶにあたって、どのような高校物理の知識が必要か解説するね。
今日は材料力学で必要な高校物理の知識について解説します。
意外と必要な知識は多く無いので、分野を絞って復習すれば大丈夫です。
この記事をおススメする人
- 材料力学を学び始めた初心者の方
- 材料力学がめちゃくちゃ苦手な方で基礎を学びなおしたい方
また下記の動画で解説していますので、是非参考にしていただければと思います。
そもそも材料力学とは
材料力学とは、材料にかかる力を議論する学問です。

当たり前やん!!
そんなツッコミが飛んできそうなのは百も承知です。
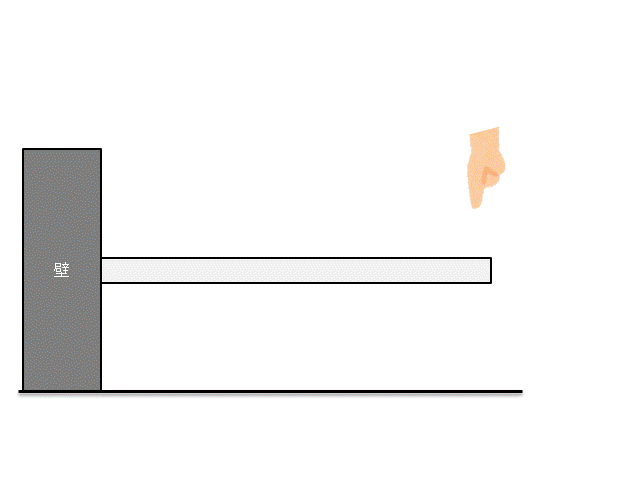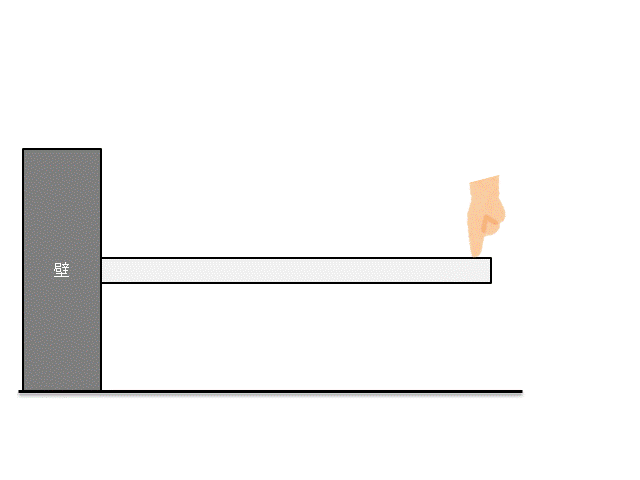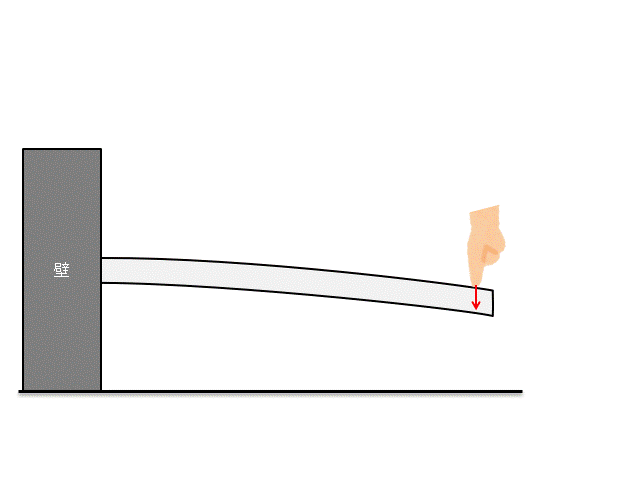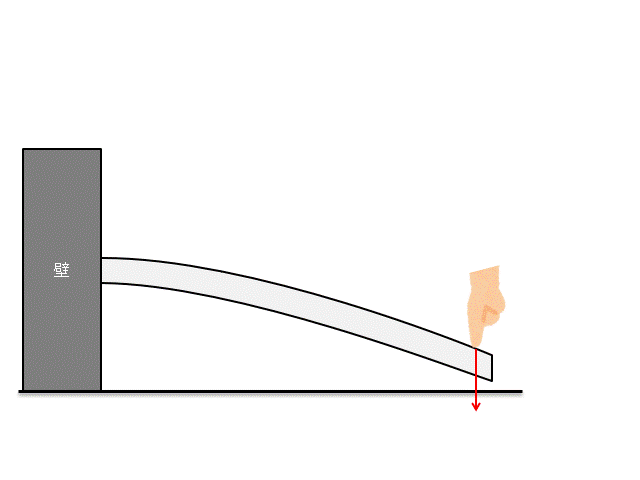
例えば下記のような片持ち梁に、力をかけることを考えましょう。
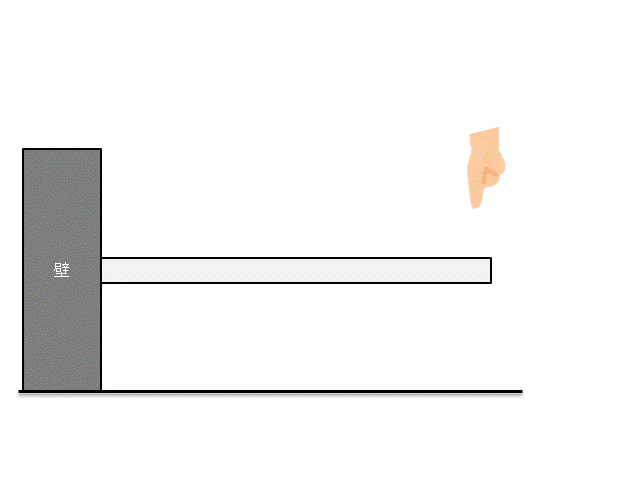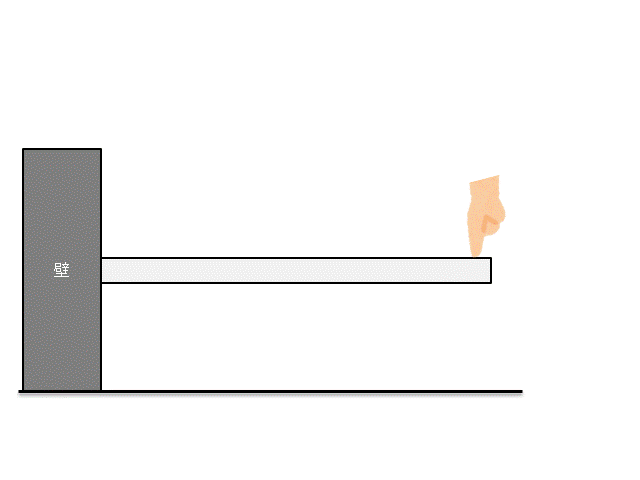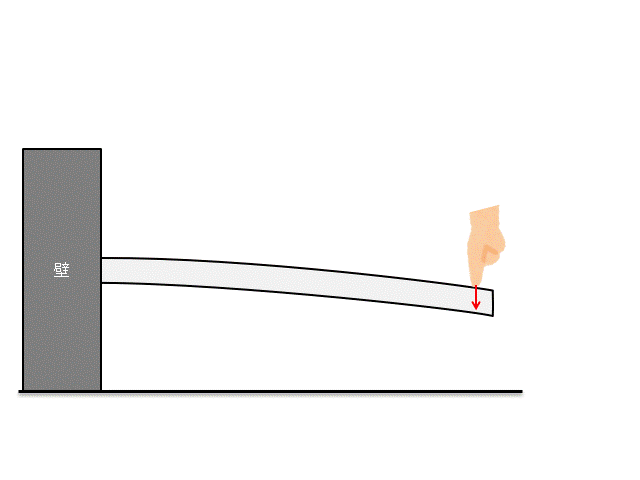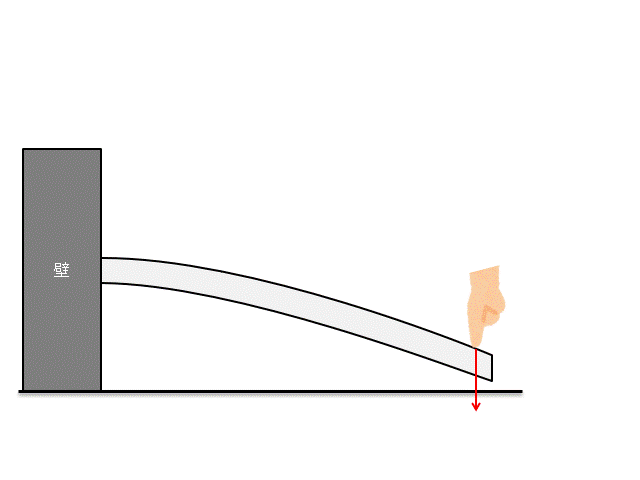
さて、この片持ち梁にどれくらいの力をかけたら壊れるかわかりますか??
この時に『○○[N]です!』と答えられるようになるのが、材料力学です。
着目している部材がどれだけの力に耐えられるか、これを議論するのが材料力学です。
材料力学で重要な2つのポイント
ポイント
- ミクロな部分に着目して、部材全体の変形を考える
- 静力学であり、力のつり合いを考えるケースが多い
上記二つは必ず頭に入れておきましょう。
厳密には動力学的な内容もやりますが、初学者の方はまずは上記2つを抑えましょう。
①ミクロな部分に着目
この片持ち梁にどんな力がかかっているかを考えるにあたって、
下図のように、とある微小な領域をとりだして考えます。
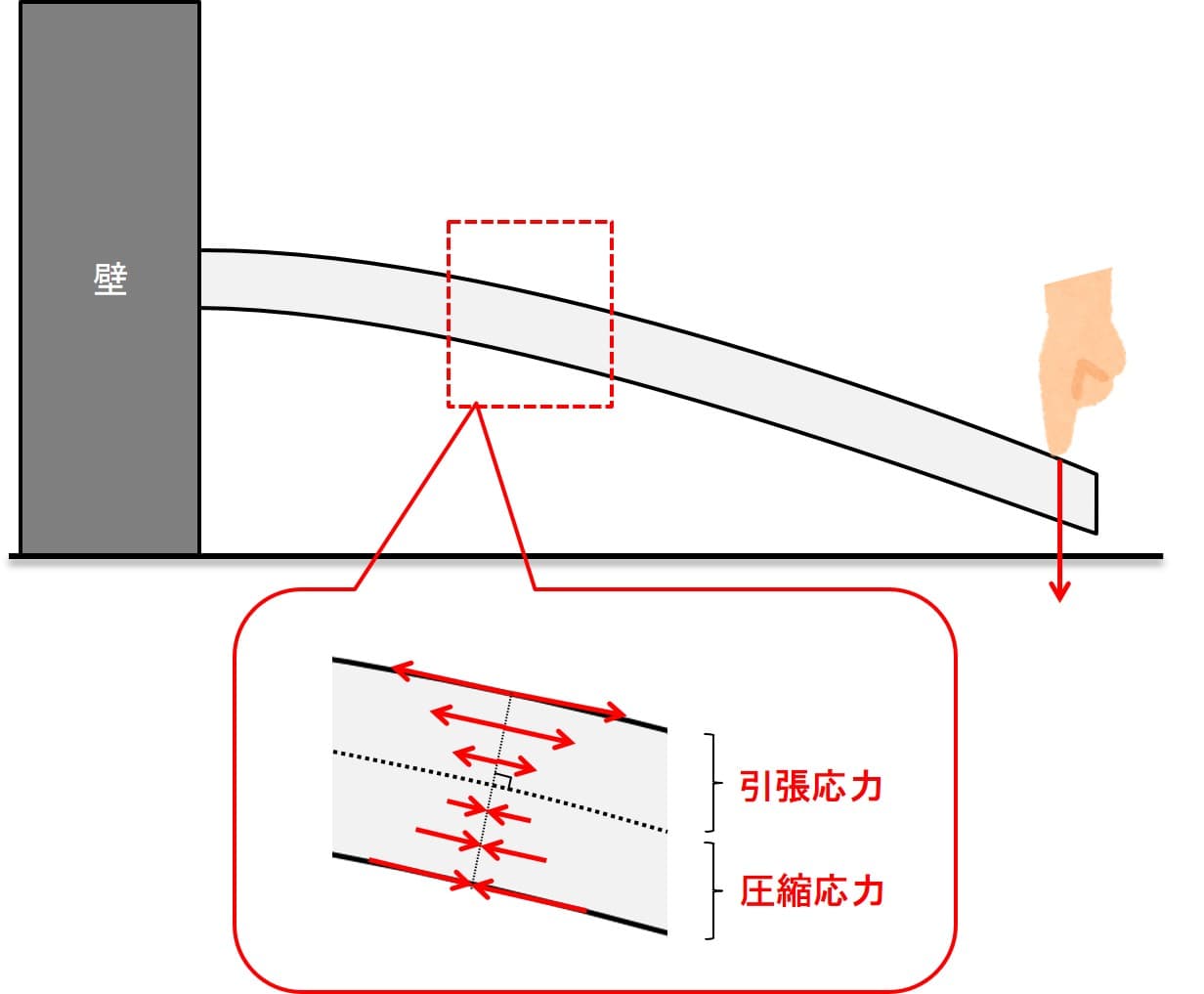
微小領域を取り扱うので、微分の概念は必須となります。
それを元に部材全体を考える、というような形になります。
この部材全体の力の状態を考える分野が、構造力学と呼ばれるものなのですが、
材料力学と構造力学の境界というのはあいまいです。
結構学ぶ内容が被っているところが多く、区別が難しいと感じることが多いと思いますが、
力を議論するにあたって、 材料と構造は切っても切り離せない部分があるので、仕方がないと思ってください。
②静力学であること
静力学と動力学の違いについては過去の記事で解説していますので、そちらを参考にしていただければと思います。
非常にざっくり説明すると、
- 静力学=力に時間依存性がない
- 動力学=力に時間依存性がある
静力学は一定の荷重などを物体に与え続けたりするような学問です。
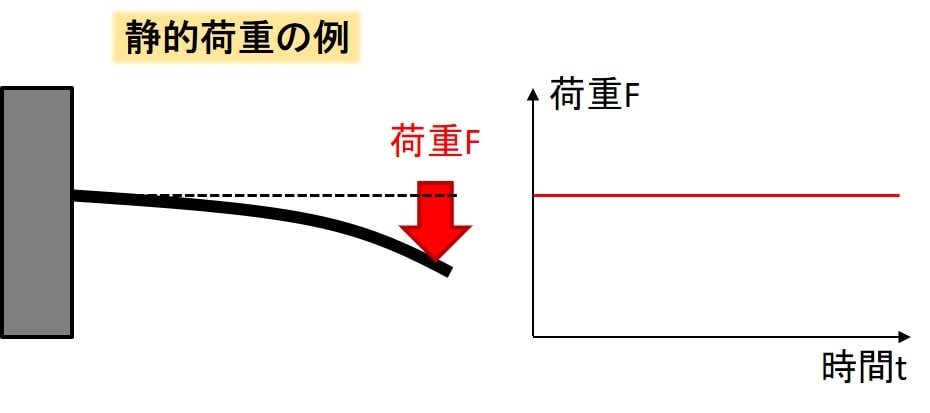
動力学の方は、例を考えていただくとわかりやすいと思いますが、振動や衝撃などを扱うような学問で、
力の大きさが時間によって変化する場合を取り扱います。
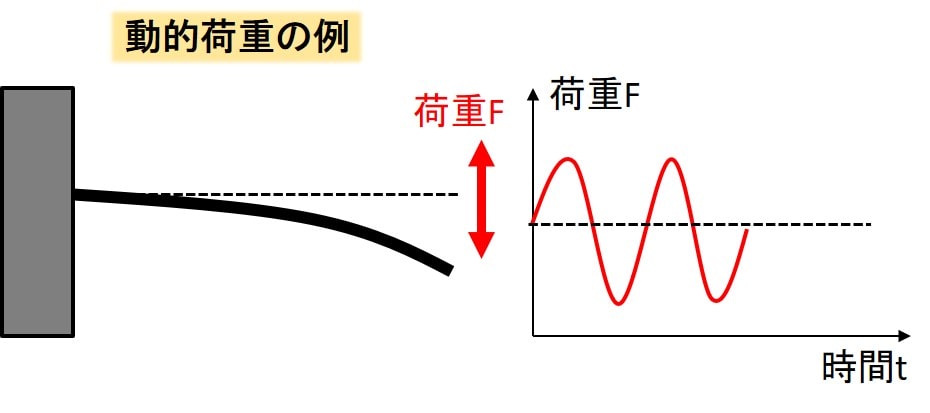
静力学のほうでは、力が一定で、材料力学では基本的に物体が止まっている状態を考えますので、
『力のつりあい』 が非常に重要になります。
この力のつりあいがキーポイントとなります。
高校物理で必要な知識
高校物理で必要な知識
- 力の概念(ベクトル)
- 力のつりあい
- 剛体(モーメント)
- 剛体のつりあい
- 物理でよく使う(ベクトル、三角関数、微分、近似など)
それではそれぞれを解説していきますね。
1 力の概念
高校物理の力学については、過去の記事でも解説しておりますので、是非そちらも参考にしていただければと思います。
力を図で書き表すとどのようになるか、下記のようになります。
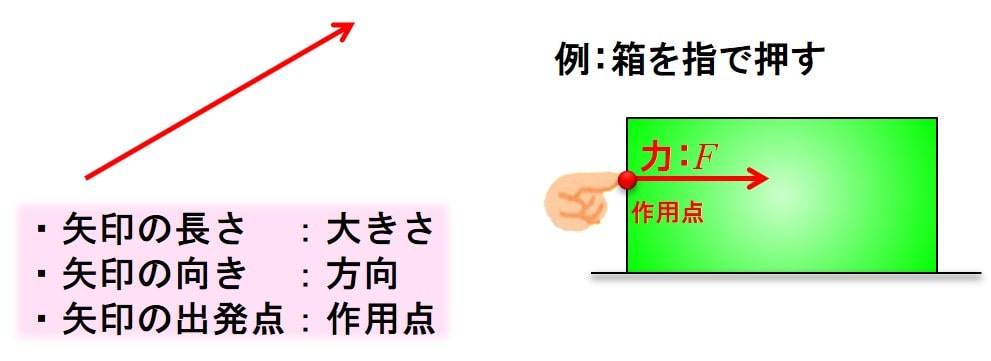
力はベクトルで表すことができ、
力のポイント
- 大きさ
- 向き
- 作用点
この3つがポイントとなりますので、しっかりと押さえておきましょう。
矢印の長さが大きさ、向きが力が働いている方向、作用点が力が発生している起点(スタート地点)ですね。
このように力をベクトルで表すと何が便利かというと、力の分解ができる、というのが1つ便利なポイントでした。
力の分解
詳細は高校物理の解説記事がありますので、そちらを参考にしていただければと思いますが、
本記事でも例を説明しておきます。
下図のように斜面をボールが転がる状態を考えましょう。
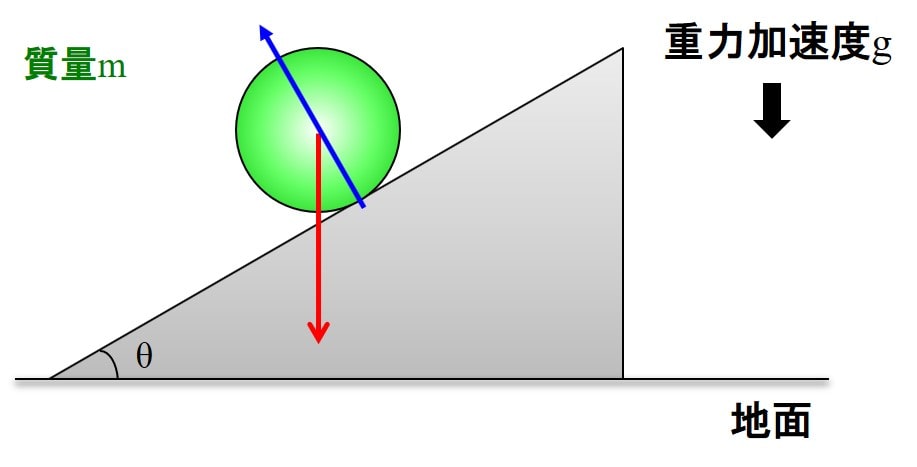
このボールにかかる力を考えると、重力加速度\(g\)、質量\(m\)とすれば、鉛直方向に\(mg\)の重力が発生します。
しかし、直感的にもこのボールは斜め方向に転がっていきそうですよね?
なので下記のように力を斜面に対して水平方向と垂直方向に分解することを考えます。
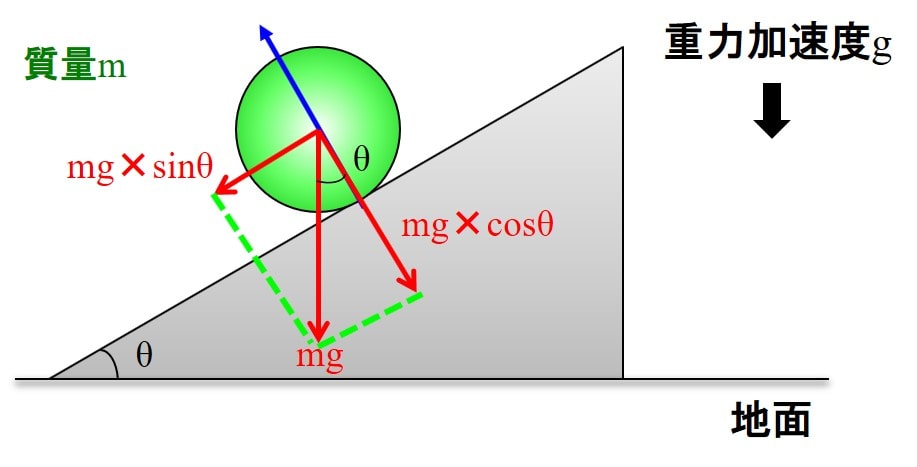
斜面と垂直方向については、斜面から受ける垂直抗力によって力がつり合っているのに対して、
斜面と水平方向については、力がつり合っていない状態になっています。
力がつり合っていない場合、物体は運動方程式にしたがって運動しますので、運動方程式を考えると、
$$F=ma$$
\(F\)は重力を斜面水平方向に分解した力となります。
\(a\)は物体の加速度で、この場合、\(a=\frac{F}{m}\)で一定値となりますので、斜面水平方向に等加速度運動をすることになります。
このように、力を分解することで、物体の運動を記述することができるようになるわけですね。
2 力のつり合い
それでは次に力のつり合いについて解説です。
力がつり合っている状態とは、物体の速度が変化しない状態、ということになります。
は??と思った方もいらっしゃるかもしれませんので、具体例で考えていきましょう。
下の図のように質点を横から押すことを考えましょう。
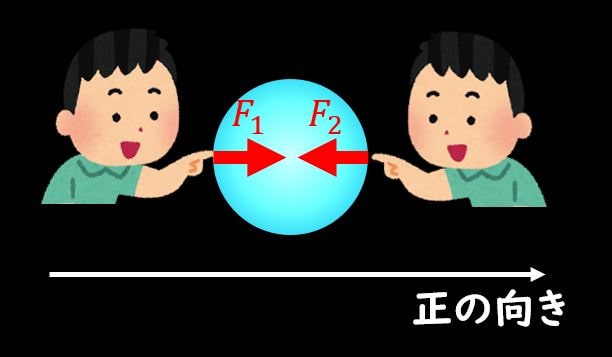
左からと右からと同じ力で押したとすると、質点に発生する力は
$$F_1-F_2=0$$
となって、合計ゼロになります。
この状態だと、運動方程式を考えた場合、加速度がゼロになるので、速度が変化しなくなる、ということになります。
初期速度をゼロとして、止まっている状態の場合は、ずーっと速度がゼロになるので、力がつり合っている時は静止した状態が続くことになります。
なお、間違いやすいものに作用反作用というものがありますので、そちらについては過去の記事を参考にしていただければと思います。
3 剛体(モーメント)
次に剛体について考えます。
剛体とは、下記のような二つの性質がありますので、しっかりと覚えておきましょう。
- 大きさがある
- 変形しない
高校物理では質点で考えることが多かったですが、一部大きさがある物体も扱いますね。
その時に重要な考え方がモーメントです。
モーメントとは物体を回そうとする力のことです。
モーメント\(M\)は下記のように表されます。
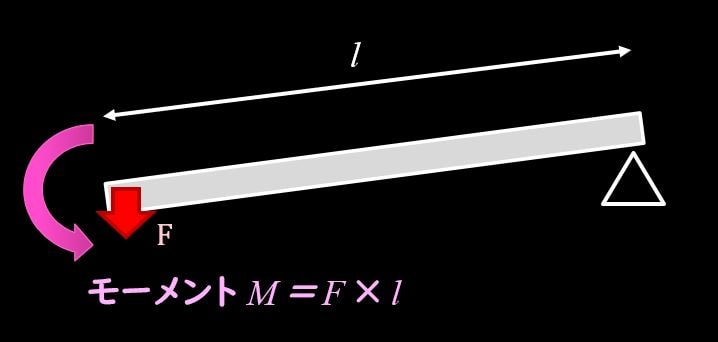
$$M=F×l$$
\(l\)は視点からの腕の長さ、\(F\)は荷重を示します。
4 剛体のつり合い
さて、モーメントが大事だということを理解いただいた上で、剛体の場合のつり合いの条件について考えましょう。
剛体のつりあいの条件は下記になります。
- 力のつり合い
- モーメントのつり合い
この二つの条件を満たすとき、剛体はつり合いの状態にある、と言います。
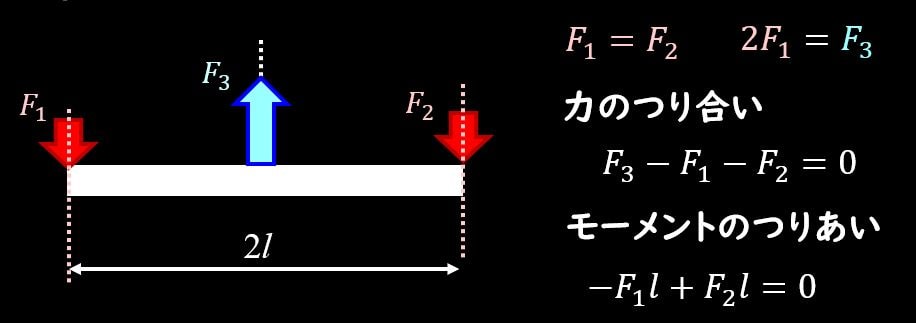
上図のような状態は剛体である棒がつりあって静止している状態になっています。
仮に\(F_3\)が無く、\(F_2\)を逆向きにすると、力だけがつり合っていても、モーメントがつり合わず回転してしまうわけです。
5 よく使う数学知識(近似)
最後に、材料力学でよく使う数学知識、矜持についてです。
三角関数や微積ももちろん材料力学では使うのですが、最低限、下記の近似を抑えておきましょう。
また、\(tanθ\)は\(x\)軸と\(y\)軸を下記のようにとると、微分の形式でも表すことができます。
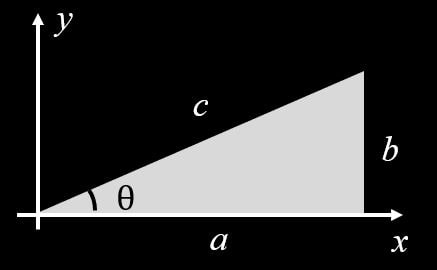
$$tanθ=\frac{dy}{dx}$$
先程の近似のように、\(tanθ≒θ\)となるので、
$$tanθ=\frac{dy}{dx}=θ$$
このように近似ができます。
材料力学では\(θ\)が非常に小さい領域を扱うことがほとんどなので、この近似は色んなところで使います。
この近似自体は大学数学でよく使うテイラー展開を用いると導出できますので、余力のある方は一度テイラー展開をやってみてはと思います。
まとめ
本日は材料力学で使う高校物理の内容を解説させていただきました。
材料力学は静力学で、基本的に力のつり合いを考える分野なので、
高校物理の中でも力学、さらにはその中の力のつりあいやモーメントのつり合いが大事であることを説明しました。
これらを抑えておけば、まずは材料力学を学ぶ準備はできていますので、
あとは材料力学を頑張って攻略していきましょう。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
次の記事 → 材料力学 応力の種類を詳しく解説-アニメーションで学ぼう
