曲げ応力がよくわからないんだけど、どういうイメージを持てばいいの?


それじゃあ今日は曲げ応力について解説するね。
本日は『曲げ応力』について解説します。
曲げモーメントによって、梁を曲げると引張応力、圧縮応力が梁断面に発生するのですが、どのような分布になるかが非常に重要です。
しっかり理解できるように解説しますので、最後までお付き合いください。
引張応力・圧縮応力については過去記事で解説していますので、そちらを参考にしていただければと思います。材料力学 応力の種類を詳しく解説-アニメーションで学ぼう
動画でも解説していますので、是非参考にしていただければと思います。梁の曲げについて
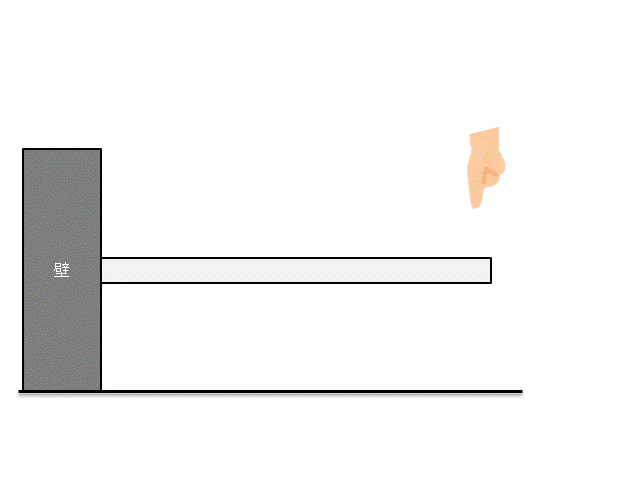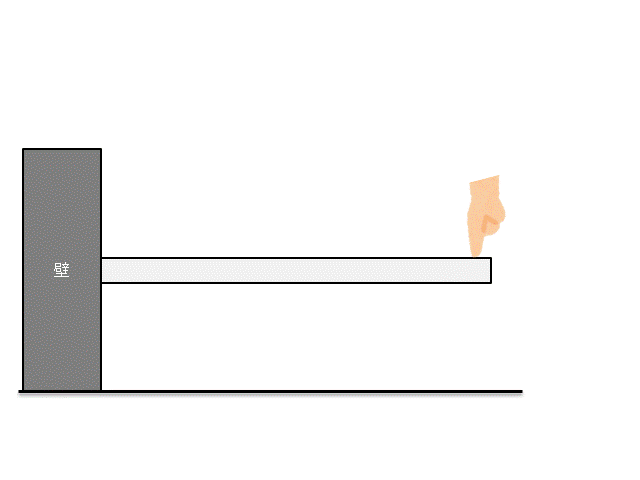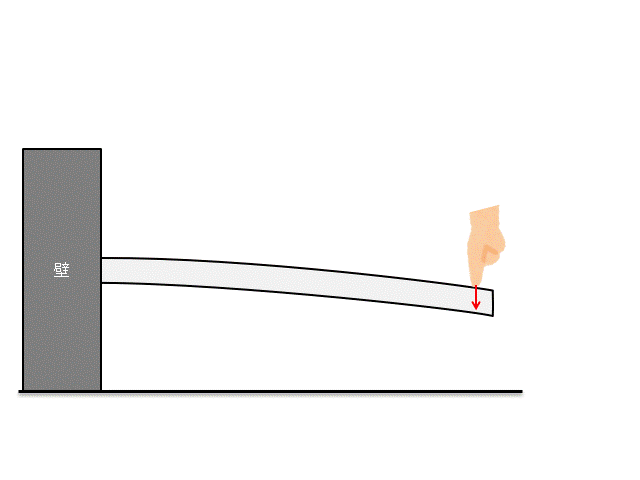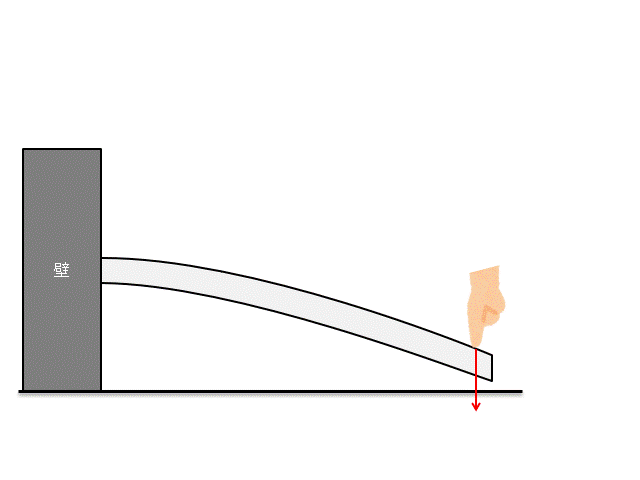
上図のように梁を曲げた時に、梁内部にどのような応力が発生するかを考えましょう。
梁面内の応力分布
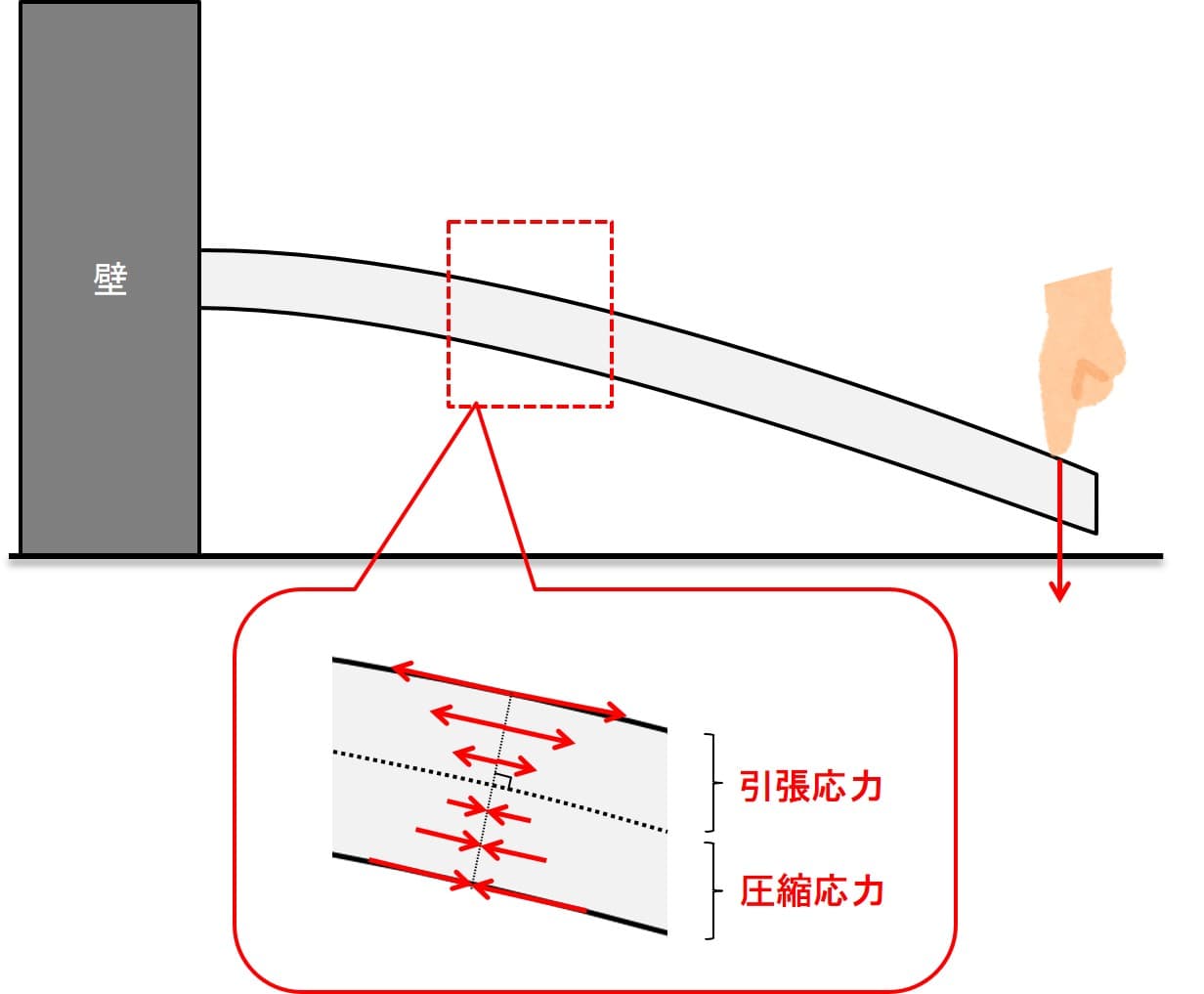
上図のような形で、 引張応力と圧縮応力が発生します。
これらを合わせて『 曲げ応力 』と呼んでいます。
中立面
梁の面内の応力分布を見てみると、上図の点線部のように引張応力も圧縮応力もゼロになっている部分があります。
この 引張応力も圧縮応力もゼロになる部分を中立面と呼びます。
曲げ応力の大きさ
曲げ応力については、最大値を下記のように表すことができます。
ちなみに厳密には『曲げ応力度』と呼びます。
$$σ_{max}=\frac{M}{Z}$$
\(σ_{max}\):曲げ応力の最大値
\(M\):曲げモーメント
\(Z\):断面係数
曲げ応力の単位は\([N/m^2]\)です。
曲げモーメントは、集中荷重を\(P\)、集中荷重を与えている点からの距離を\(L\)とすると下図のように表されます。
$$M=P×L$$
断面係数\(Z\)は、断面形状によって決まります。
代表的な断面係数を下図に示します。
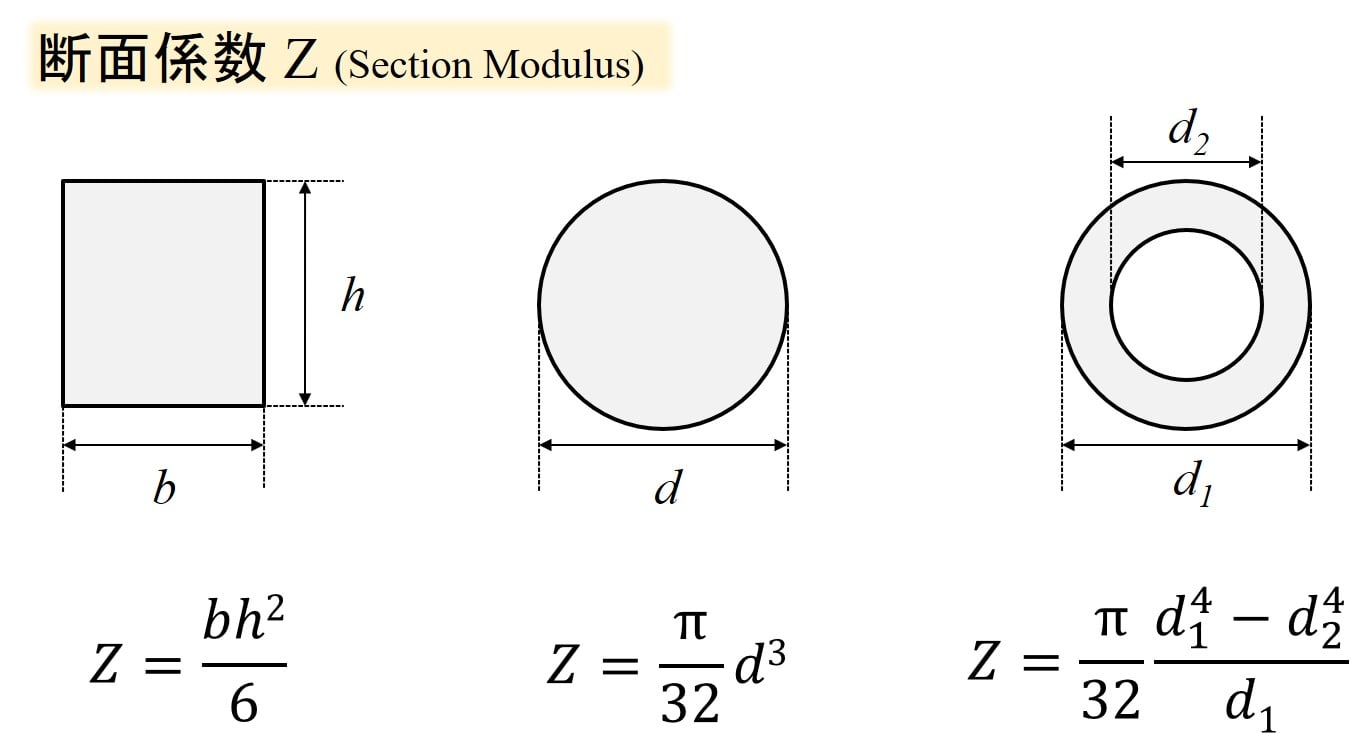
全ての断面係数を覚える必要はありませんが、断面によって異なるということはしっかりと頭に入れておきましょう。
長方形の断面係数については、力を加える方向によって注意が必要です。

曲げ応力はなぜ最大値だけ考えるの?
実際に曲げ応力の計算をするケースというのは、『 曲げた時に壊れないように設計したい』、というケースが多いです。
そして 壊れる、壊れないの判断をするには、材料に発生する最大応力が重要になるからです。
例えば、『塑性変形=壊れた』とするならば、梁に発生する最大応力が、塑性変形を起こす応力を超えてしまうかどうか、が判断のポイントになりますね。
塑性変形などの解説については過去の記事を参考にしていただければと思います。
材料力学 応力-ひずみ曲線と塑性変形、弾性変形をわかりやすく解説
まとめ
曲げ応力について解説しました。
梁を曲げた時、梁の断面に発生する引張応力・圧縮応力を曲げ応力と呼びました。
この曲げ応力の最大値は下記のように表されます。
$$σ_{max}=\frac{M}{Z}$$
\(M\)は曲げモーメント、\(Z\)は断面係数となります。
長方形断面のときには、どちら向きに曲げモーメントが発生しているかを意識しましょう。
この最大曲げ応力を考えて、曲げても部材が壊れないかどうかの設計をする、というケースが多いので、
曲げ応力の考え方をしっかりと理解しておきましょう。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
