材料力学 応力の種類を詳しく解説-アニメーションで学ぼう

今回は材料力学の『応力』についてです。

『応力』は高校物理で習った『力』とは別モノです。

材料力学ではいろんな応力が出てきますので、それぞれ解説しますね。

下記動画でも解説していますので、参考にしていただければと思います。

内力、応力、応力度

内力、応力、応力度という3つの単語の違いを整理しておきましょう。

• 内力=応力
• 応力度は単位面積当たりの応力

厳密にいうと『応力』と『応力度』は異なりますが、口語で応力、応力というときは応力度のことを指すことも多いです。

以下、応力度のことを応力と示します。

応力（Stress）について

次のような四角柱を縦に伸ばすことを考えましょう。

四角柱の断面積を\(S\)とし、上下に力\(F\)で引っ張るとします。

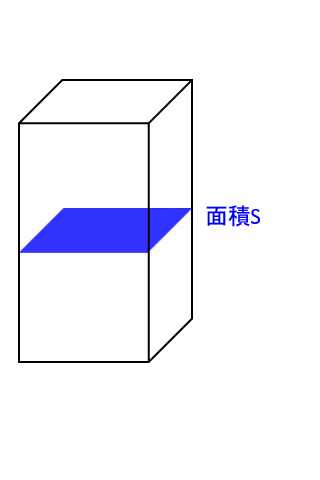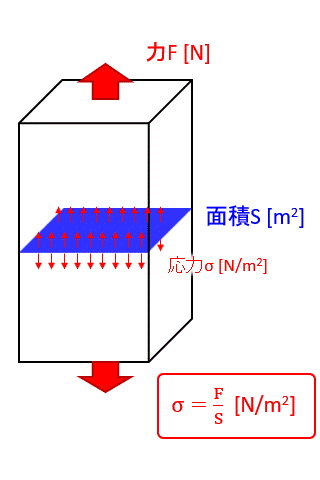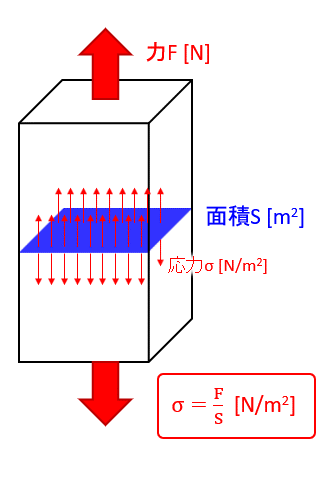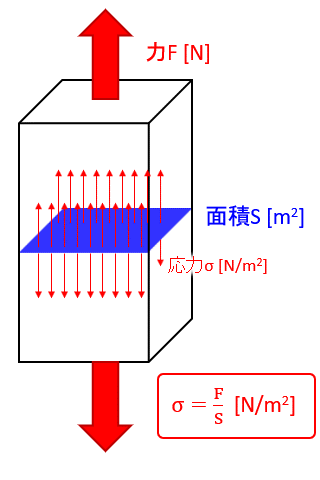
このときの応力をσ（シグマと読みます）で表すと下記のようになります。

$$σ=\frac{F}{S}$$

この引っ張っているときの応力を引張応力と言いますが、あとでまとめて解説しますね。

応力と圧力の違い

そう、圧力とすごく似ていますが、厳密には違います。

図のように、圧力は外部から力を受けた表面にかかる力、応力は固体内部にかかる力を示します。

固体の表面を固体内部の中にひっくるめることもあるので、圧力は応力の一種です。

応力の種類

応力の種類は5種類で分類します。

この5つです。順に解説していきますが、今回はねじれについては別記事で解説させていただきますね。

引張応力と圧縮応力

この二つは兄弟です。

図で見てみましょう。

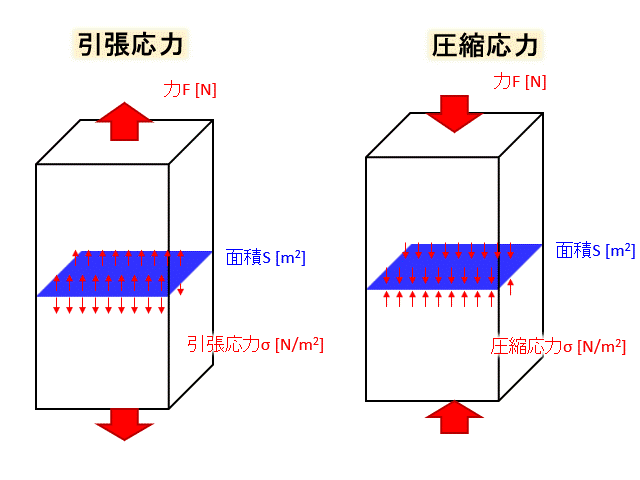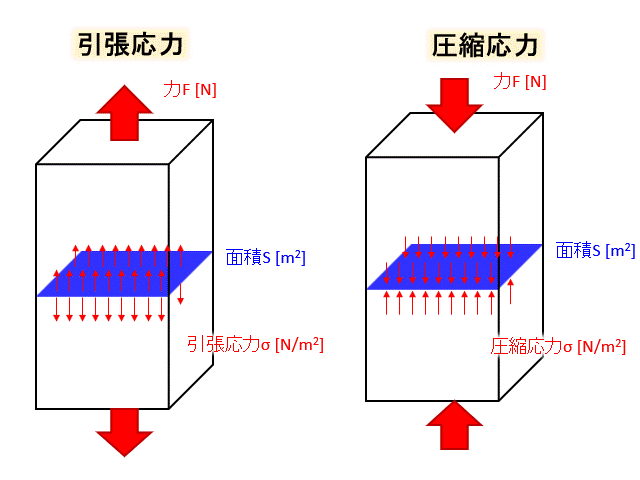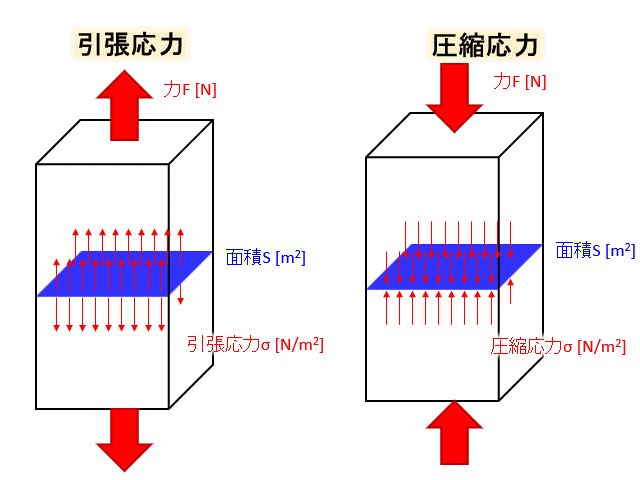
このように引っ張るか押しつぶすか、力の向きによって引張応力、圧縮応力と呼びます。

引張応力も圧縮応力も応力の大きさはσは

$$σ=\frac{F}{S}$$

となります。

せん断応力

このせん断応力がイメージしづらいところだと思いますので、丁寧に解説します。

そもそもせん断（剪断）って何？って話ですが、

モノが切断されることをせん断と呼びます。

ハサミとか穴あけパンチのような力がせん断力です。

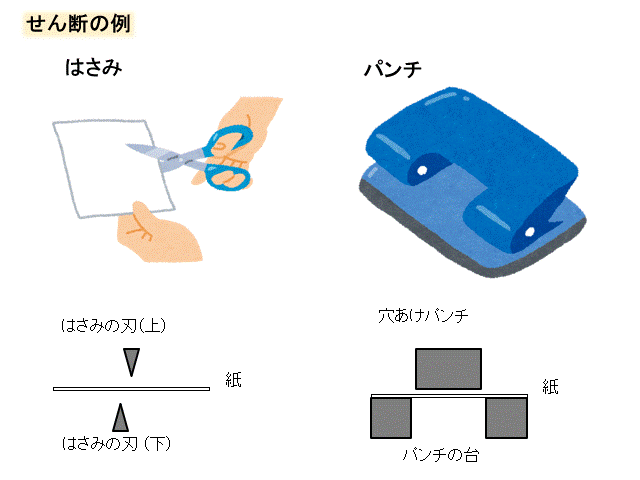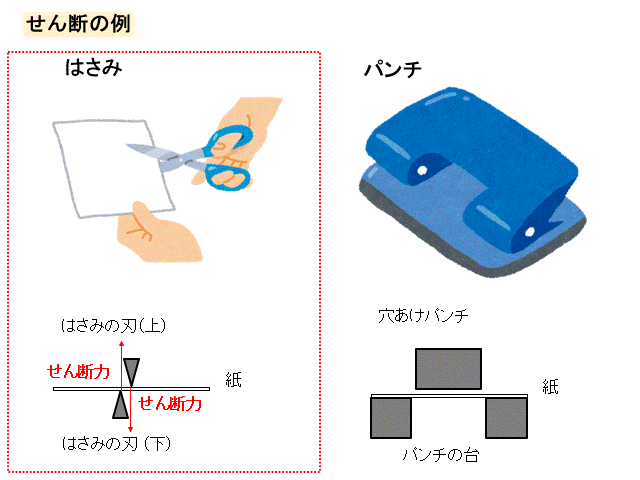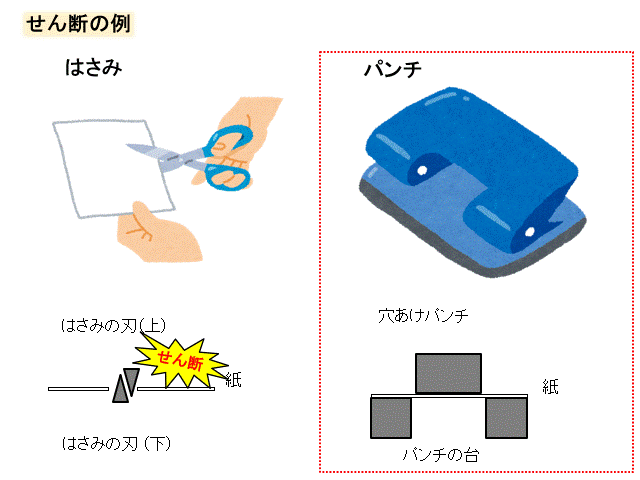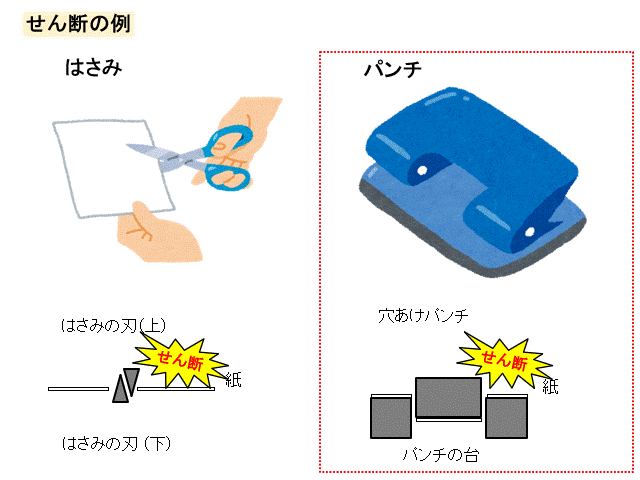
せん断応力はτ（タウと読みます）で表され、せん断力を\(F\)、断面積を\(S\)とすると、

$$τ=\frac{F}{S}$$

こちらも力を断面積で割ることになります。

曲げ応力

曲げ応力とは、曲げたときに発生するときの応力です。

そのまんまですね笑

曲げるために発生した曲げモーメントに対する反作用的な力、と覚えてください。

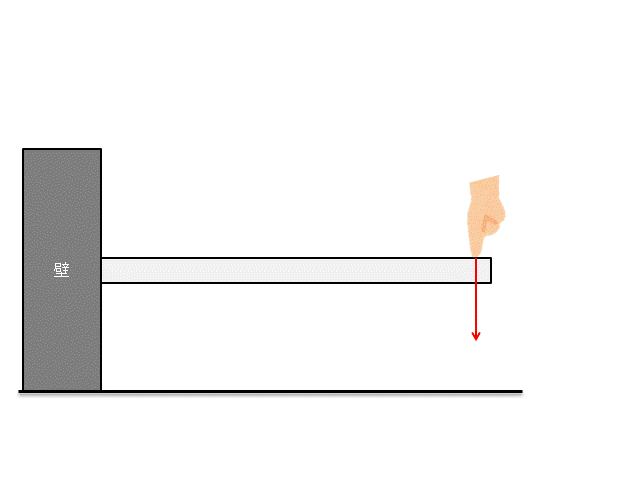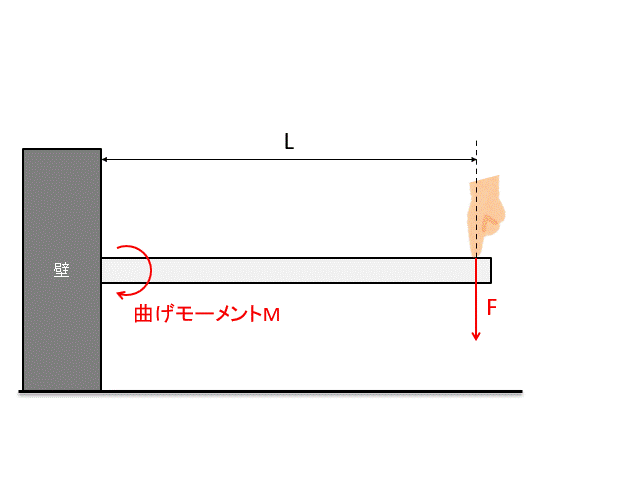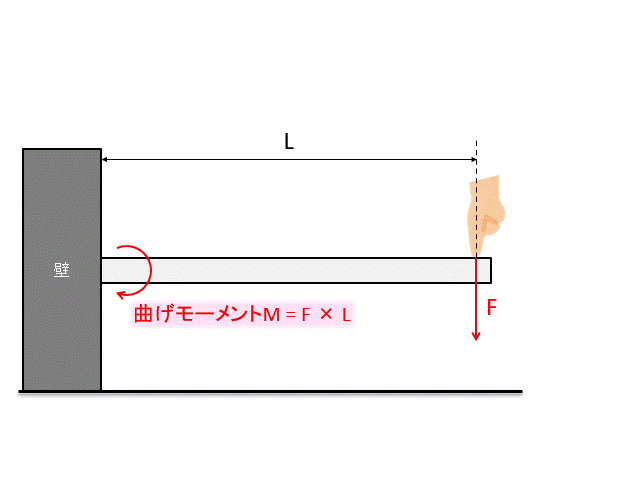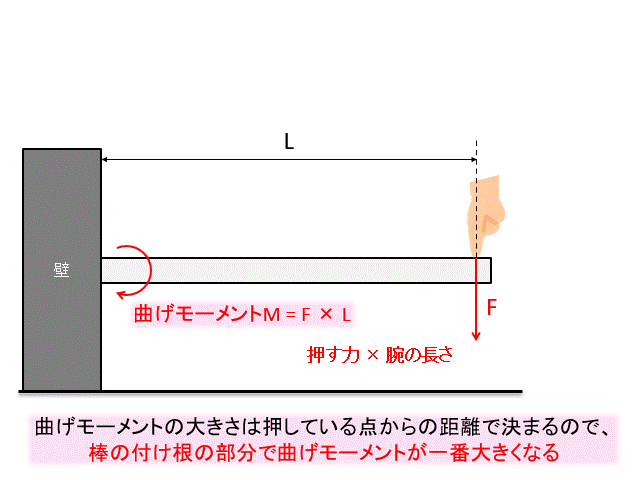
下図のように、壁に片側だけ固定した棒の先端を押して、棒を曲げることを考えましょう。

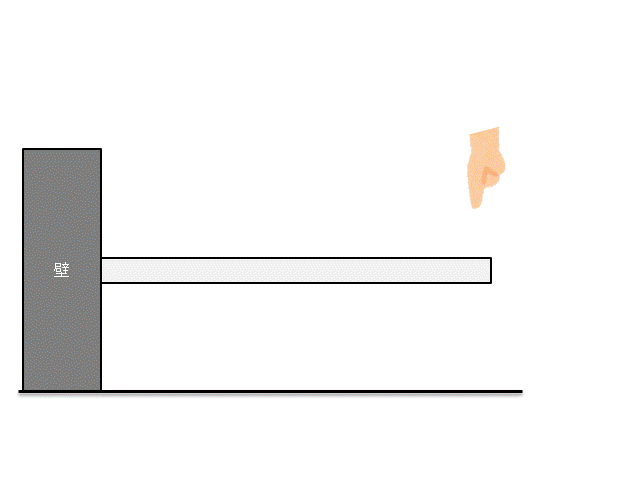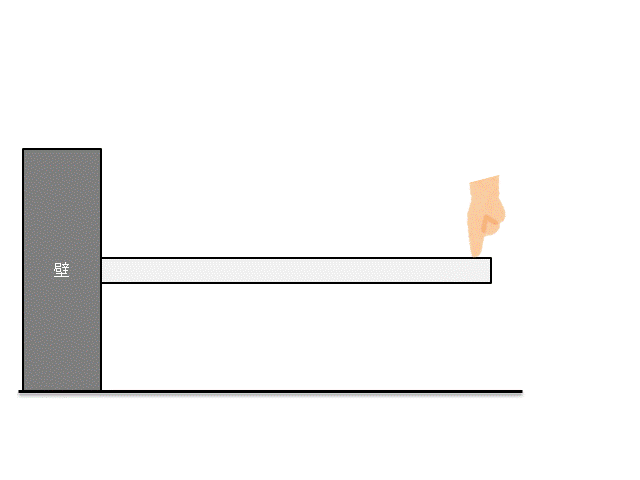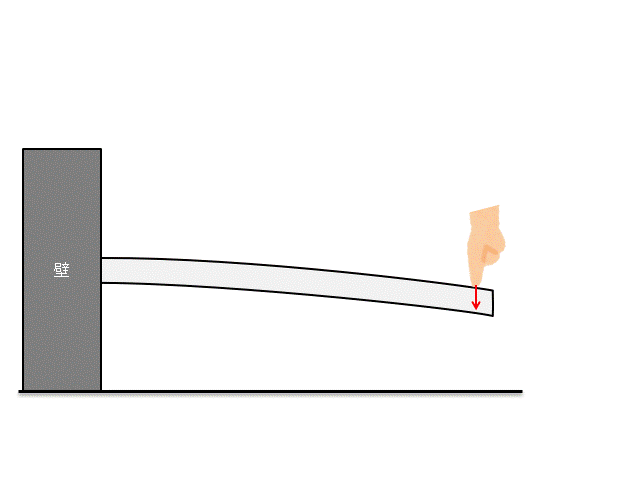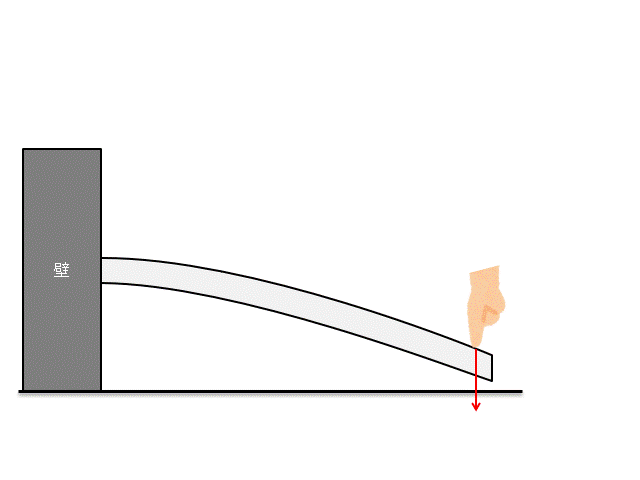
このように棒を曲げたときの曲げ応力を考えます。

下図の赤枠で囲った部分の応力がどうなっているか見てみましょう。

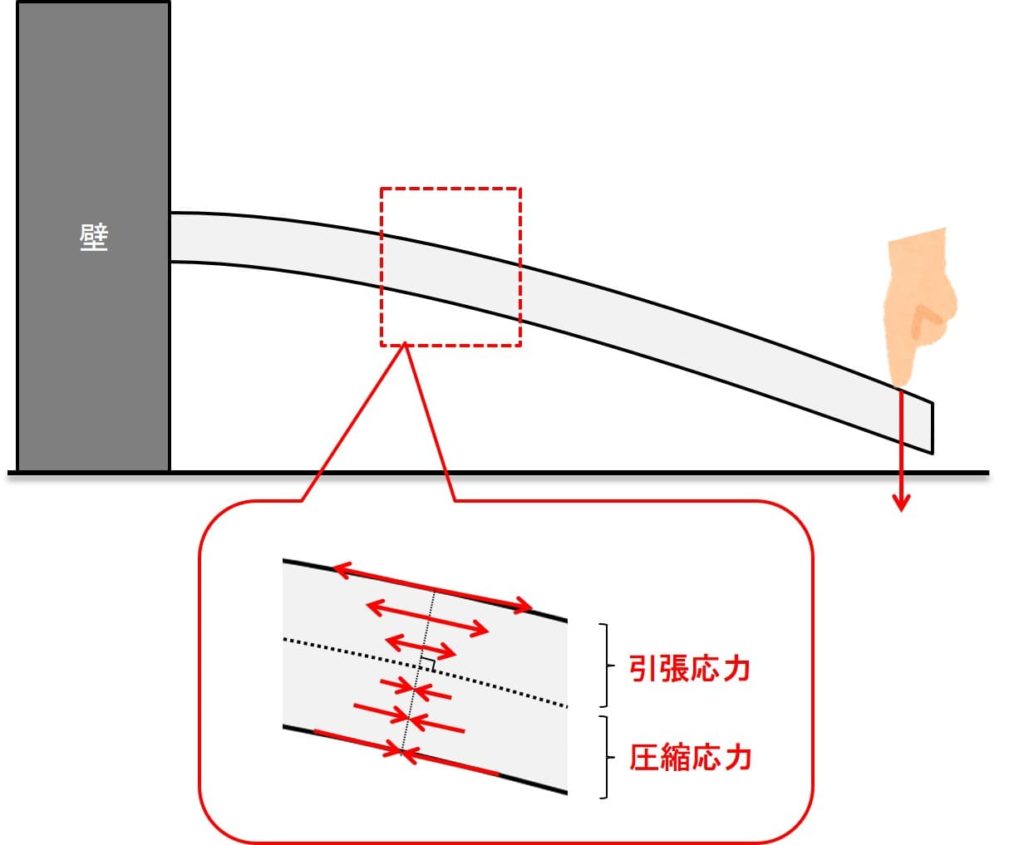
棒を上から押すと、棒の上側は面内で引っ張られ、下側は面内で圧縮方向に力がかかります。

それでは最大の曲げ応力を求めてみます。

最大曲げ応力ですが、下記のような式となります。

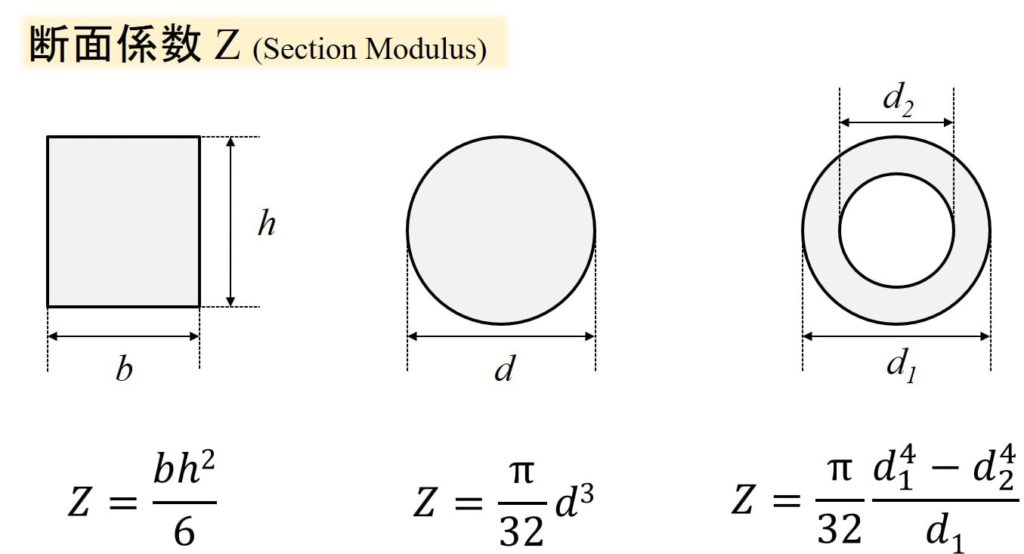
$$σ_{max}=\frac{M}{Z}$$

最大曲げ応力を\(σ_{max}\)、\(M\)を最大の曲げモーメント、\(Z\)を断面係数としています。

曲げモーメントは押す力×腕の長さで求まりますね。　

押す力は一定で\(F\)とすると、腕の長さが長くなるほど曲げモーメントは大きくなります。

どこに一番大きなモーメントが発生するかですが、片方の端部を固定している場合、棒の付け根の部分に一番大きな力が発生します。

腕の長さが一番長くなる部分が付け根の部分なので、曲げモーメントは付け根で一番大きくなります。

この曲げモーメントを断面係数で割ることで、最大応力が求まります。

曲げ応力は、曲げモーメントに拮抗する力（曲げモーメントの反作用の力）になるので、曲げモーメントを考えればよいわけです。

断面係数は、断面の形状による曲がりやすさを示したものです。

これについては各形状で導出できるのですが、今回は割愛します。

下に断面係数をまとめておきますね。

まとめ

本日は応力の種類について解説しました。

応力は固体内部に発生する単位面積あたりの力で、下記の種類があります。

引張と圧縮は向きが違うだけ、せん断応力は断面と同じ向きの力による応力、曲げ応力は棒などを曲げたときに発生する応力です。

今回はねじれたときに発生するねじれ応力は割愛しました。

まずは応力ってどんなイメージかを理解して、詳細について深堀していただければと思います。

材料力学の基礎の基礎なので、しっかり理解しましょうね。

初心者向けの参考書・教科書をこちらで紹介していますので、書籍選びに迷っている方は参考にしていただければと思います。