力学ってよくわからん・・・なんか矢印いっぱい出てくるし、これ何なの?


力学の矢印はベクトルで表すんだ。これがわからないと力学がさっぱりわからなくなるので、丁寧に説明するね。
本日は、力学での最初の関門、ベクトルについてです。
中学まででは習わなかった分野の数学が、物理で先に出てくるということを体験した人は多いのではないでしょうか?
私もそうでした笑
ここでつまづくと、この先ずっと物理がわからなくなりますので、しっかり解説していきます。
本記事をおススメする人
- 力学を学び始めた方で、ベクトルが出てきて困っている
- 授業の予習でどんな感じかをつかみたい人
力の表し方
先にポイントを3つ示しますね。
力の表し方のポイント
- 力の大きさ
- 力の向き
- 力の作用点(出発点と作用線)
つまり、わかりやすく言い換えると、
『 どれくらいの大きさ』の力が、
『 どの向き』に、
『 どこに』かかっているのか?
この3つがわかれば、力を表すことができるということになります。
『力』のポイントの例
『力学』とは『力』を扱う『学問』です。
じゃあ力って、なんなの??という疑問が出てくると思いますが、
力とは、『 物体を変形させたり、速度を変化させたりするもの』です。
指で床に置いてあるボールを、ゆっくり押してみましょう。
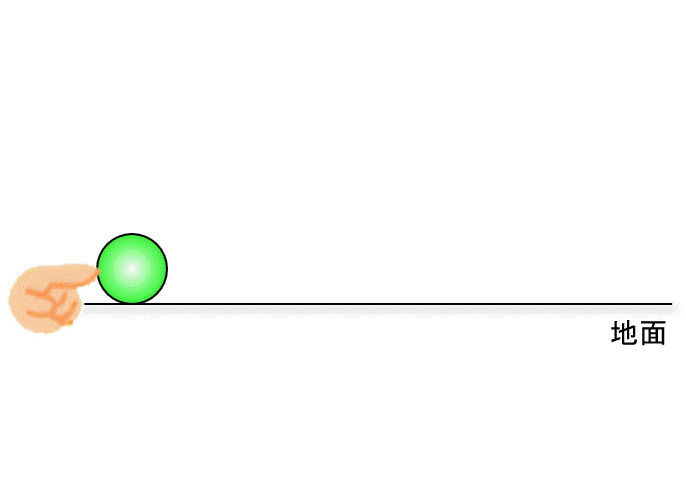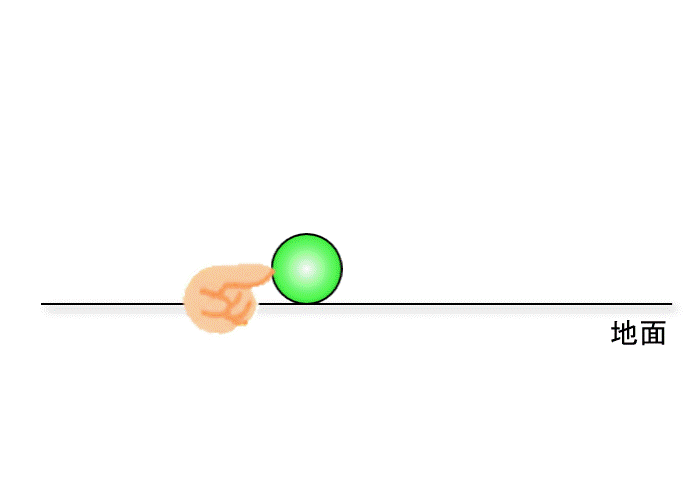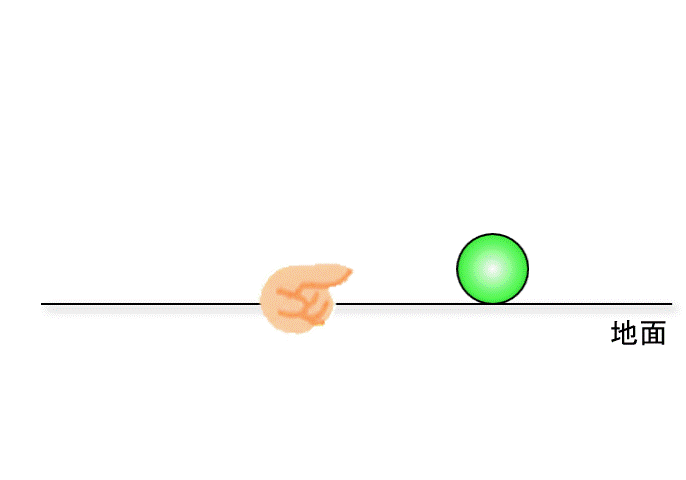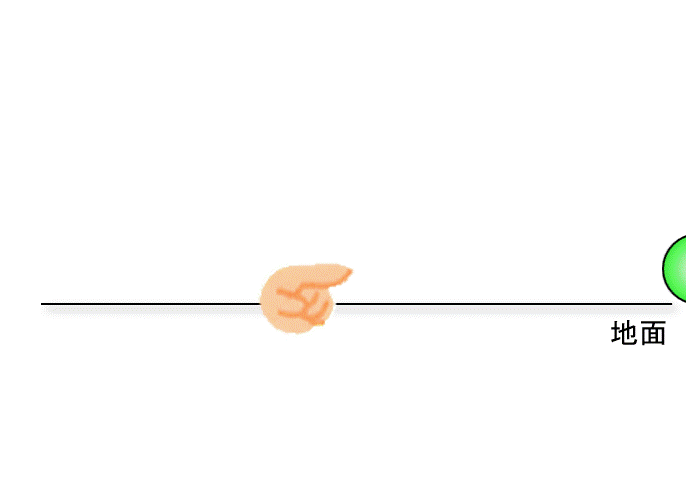
ボールは止まっている状態から、ある速度で転がるようになります。
では、この時の力ってどういうものなの?
っていうときにどういう説明をすればよいかというと、
先ほどの3つのポイントを説明すればOKなのです。
『 どれくらいの大きさ』の力が、
『 どの向き』に、
『 どこに』かかっているのか?
今回の場合、力の大きさを100N(ニュートン)とすると、
『100Nの大きさの力』が
『右向き』に
『ボールの側面に』かかっている
ということになります。
ベクトルで表す
先ほど力をイメージできるように、例を示しましたが、
3つのポイントを表すのに便利な道具が、ベクトル、というものなのです。
書き方をまとめると下の図のようになります。
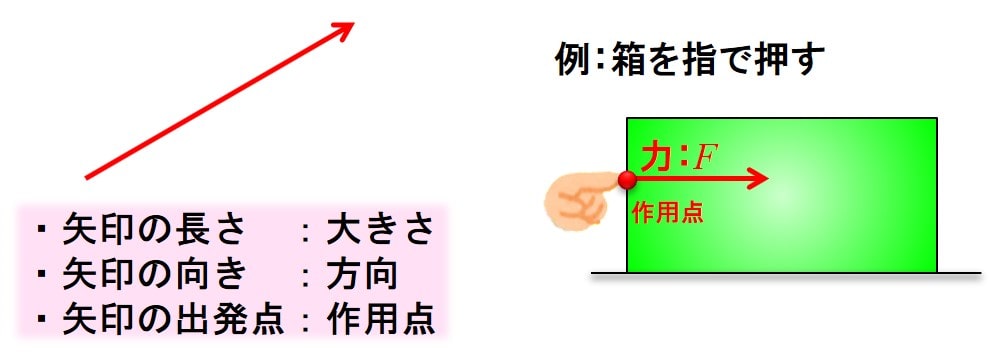
矢印の『長さが大きさ』、矢印の『向きが方向』、矢印の『出発点』が作用点です。
力は英語でForce (フォース)なので、頭文字のFを使って表します。
また、ベクトルの表し方として、Fの上に矢印をつけて \(\vec{F}\) と書くことを覚えておきましょう。
座標とベクトル
ベクトルを表す際に、下記のように書くことがあります。
$$\vec{F}=(x,y)$$
$$\vec{F}=(x.y,z)$$
この表記のポイントについて先に示しておきます。
ベクトルの成分表示の仕方
\(x\)方向の成分= 終点の\(x\)座標 - 出発点の\(x\)座標
\(y\)方向の成分= 終点の\(y\)座標 - 出発点の\(y\)座標
何コレ?座標??ベクトルって座標で書くの?


う~ん、厳密には座標表示ではないんだ。座標のように書くことを『成分表示』、と言うんだ。成分で書くと、向きと大きさを指定することができるんだよ。
下記に具体的な例を示しますね。
座標の軸を下記のように設定して、ボールを斜め下から指で押します。
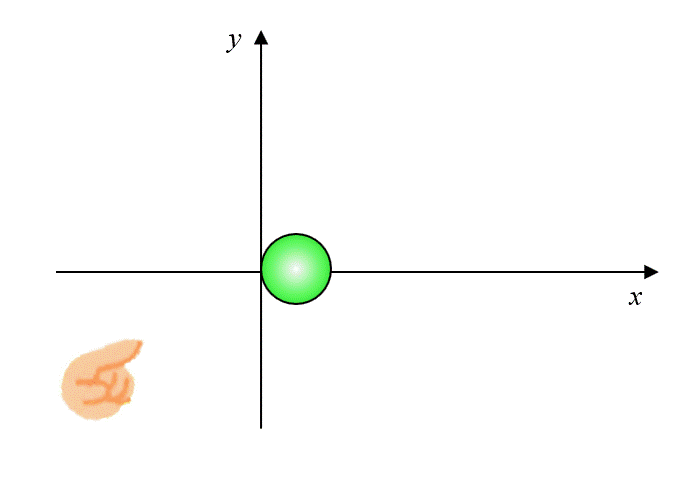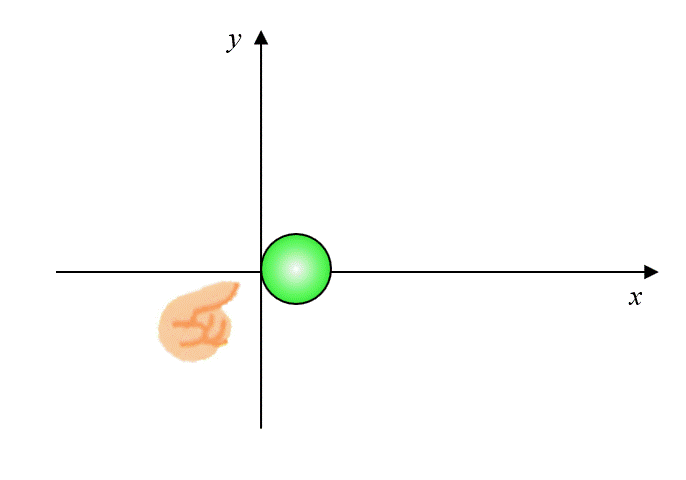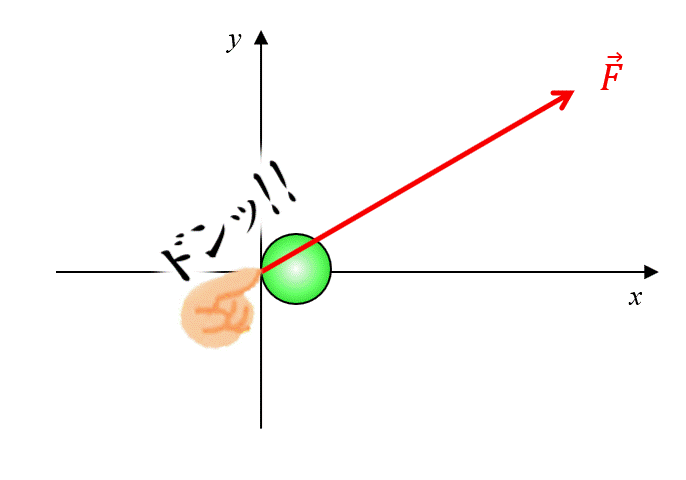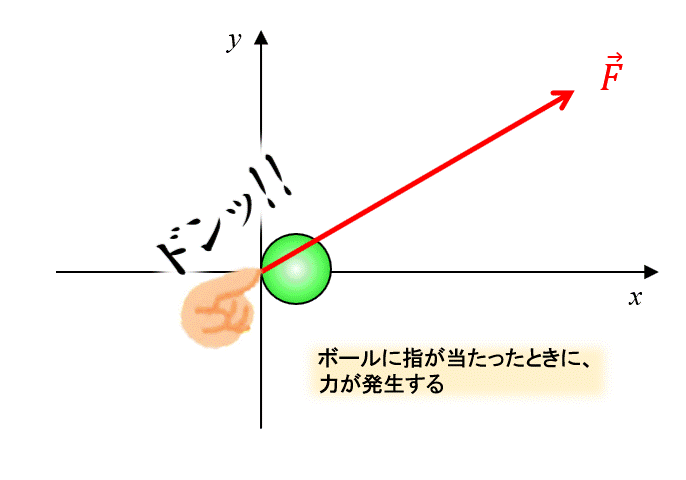
そうすると斜めの力\(\vec{f}\)が発生しますね。
さて、このベクトルを座標で考えましょう。
ベクトルの終点(矢印の先っぽ)の座標を下記のように、\((x,y)=(4,3)\)とします。
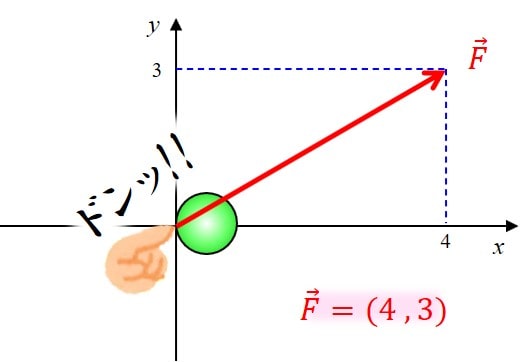
このように表記すると\(\vec{f}=(4,3)\)となります。
今回の\(\vec{F}\)というベクトルは『\(x\)方向に4、\(y\)方向に3進むようなベクトル』という意味です。
この\(\vec{F}\)の大きさは、矢印の長さなので、三平方の定理(ピタゴラスの定理)から、5となりますね。
でもこれって原点を作用点にとらなきゃいけないの?


座標軸、つまり原点の設定というのは自由に設定していいんだよ。問題によって解きやすい方向に設定するんだ。
でも、問題によって解きやすい方向なんて、いきなりわからないよ・・・


大丈夫、問題によって、とは言ったけど、最初に水平方向と縦方向に座標軸をとると8割くらいは上手くいくよ。
『座標軸はどのようにとってもいい』
この座標軸を自由に設定できる、というところが、物理を難しくしているところだと思います。
例えば、原点を下記の紫色で示した軸のように、左側に1、下側に1ずらしたところにとっても良いわけです。
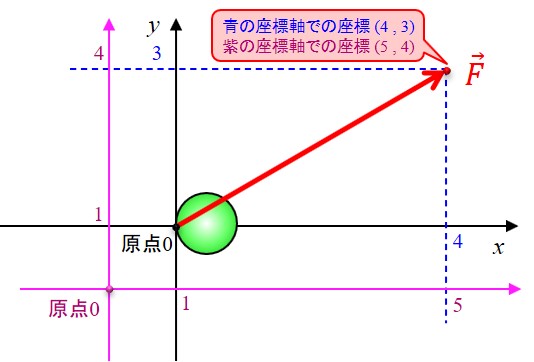
この時、\(x\)方向の成分は、\(5-1 = 4\)となります。
先ほどのように、\(x\)座標が5だから、\(x\)の成分が5とはなりません。
え?なんで??5じゃないの?


\(x\)方向で見てみると、0~1の間にはベクトルが無いでしょ?無い区間の成分はちゃんと引かないといけないんだ。
ということで、\(x\)方向の成分は、5-1 = 4です。
同様に、\(y\)軸方向の成分は4-1 = 3です。
つまり、\(\vec{f}=(4,3)\)で、大きさは5で、先ほどと変わりません。
まとめると、各成分を書くときは、
- \(x\)方向の成分= 終点の\(x\)座標 - 出発点の\(x\)座標
- \(y\)方向の成分= 終点の\(y\)座標 - 出発点の\(y\)座標
このようになります。
そのほかのベクトルの操作
ベクトルの合成と分解
ベクトルは合成と分解ができます。
分解については過去記事を参考にしていください。
このあたりの知識が力学では必要になりますので、マスターするためにも問題をたくさん解くようにしましょうね。
力と作用線について
作用線上の力ベクトルは平行移動することができる、ということを学んだ方は多いと思います。
実際、力のつり合いを考えることで適応できる話なので、覚える必要は無いです。
正直、筆者はこの考え方は好きではありません。
力には作用点という大切な要素があるのに、作用線上でなんでもかんでも平行移動させるのは、本質ではないです。
なぜ作用線上を平行移動させてもOKなのか?
このことについては、後日詳細を記事にする予定です。
まとめ
以上、力の表し方について説明させていただきました。
力を表すにはベクトルを使用します。
ベクトルは、『大きさ』、『向き』、『出発点(作用点)』の3点が重要なポイントです。
また、ベクトルを成分表示するときの注意事項も解説しました。
ベクトルの成分表示の仕方
\(x\)方向の成分= 終点の\(x\)座標 - 出発点の\(x\)座標
\(y\)方向の成分= 終点の\(y\)座標 - 出発点の\(y\)座標
軸の取り方は自由です。
自由な分、どのように設定するかが重要になってきます。
問題によっては座標軸の取り方をミスすると、計算が複雑になりすぎて、時間的に詰むことがあります。
是非、問題をたくさん解いて、力の表し方、座標軸の取り方をマスターしてください。
この記事を読んだだけでは、武器を手に入れた状態です。
レベルを上げるには問題を解くという地道な作業が必要ですので、がんばりましょう。