静的・動的っていう言葉が出てきたんだけど、違いが良くわからないんだけど…


これは材料力学と振動力学との違いにもつながるところだね。
今日は静的・動的の違いを解説しますね。
本記事では静的・動的という概念について解説します。
静的・動的というのは、荷重の種類を示すことが多く、 先にポイントを示しておくと
- 静的荷重:材料力学の分野で扱う
- 動的荷重:振動工学の分野で扱う と大まかにとらえて頂いて差し支えありません。
これらの取扱いについて解説していきます。
静的荷重と動的荷重の区別 これらの区別は『荷重が時間変化するかどうか』ということがポイントです。
静的荷重の例
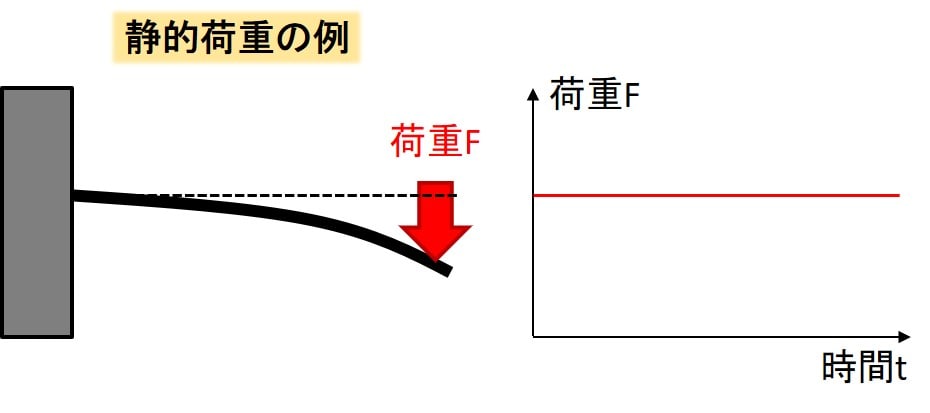
この図は片持ち梁の先端にずーっと同じ力を与え続けています。
このケースでは与えている荷重は時間変化しておらず、静的荷重と呼びます。
材料力学の分野で学ぶ内容は、基本的には静的荷重を取り扱います。
(人によっては、振動も広義の材料力学として扱う方もいらっしゃいますので、ご注意を)
静的荷重の場合の変位量xは下記のようになります。
$$F=kx$$
\(k\)は片持ち梁の剛性を示していて、フックの法則と同じですね。
動的荷重の例①振動
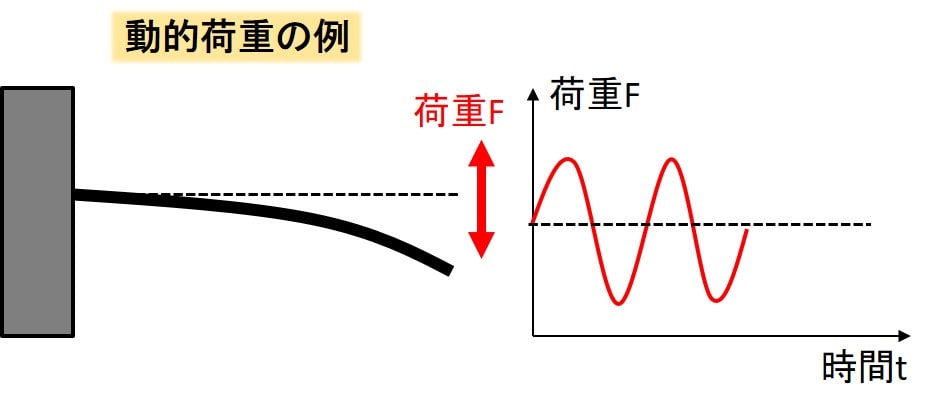
この図は片持ち梁の先端に周期的外力を与えています。
こちらのケースでは、与えている荷重は振動となるので、時間変化しております。
このように時間変化している荷重のことを動的荷重と呼びます。
振動工学や機械工学で取り扱うことが多い内容です。
振動のような動的荷重の場合、共振現象が発生します。
この現象が工学的にも非常に重要で、振動設計には欠かせない現象となっています。
強制振動については下記の過去記事を参考にしてください。
また動画でも解説していますので参考にしてください。
この共振は周期的外力の周波数と、揺れる対象の固有振動数が一致したときに、 振幅が大きくなる現象です。
強制振動のモデル、運動方程式を書くと下記のようになります。
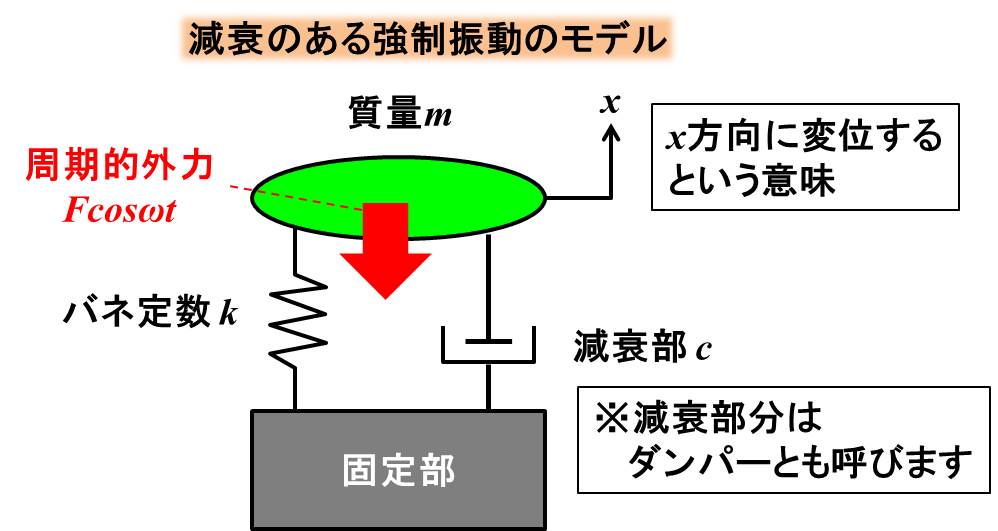
$$m\ddot{x}+c\dot{x}+kx=Fcosωt$$
この運動方程式を解いて、変位の式を求めると下記のようになります。
$$x(t) = C_1 e^{λ_1 t}+C_2 e^{λ_2 t}+\frac{f}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}sin(ωt-δ)$$
$$f=\frac{F}{m}$$
第1,2項は減衰の自由振動成分となりますので、定常状態(時間がある程度たったとき)では、 振幅がゼロとなり無視できます。
第3項が定常状態での変位を示す項となります。
この式で周期的外力の周波数を示すωと、振動体の固有振動数を示す\(ω_0\)が一致すると、 振幅の分母が小さくなり、振幅が増大します。
これが共振と呼ばれる現象です。
この共振したときの振幅の大きさを表現するときに、静的荷重の場合と比較して何倍になっているか、 という表し方をすることがあります。
いわゆる増幅倍率とよばれるものですね。
静的荷重の変位量を\(x_{st}\)、動的荷重の変位量を\(x_d\)とすると
$$x_{st}=\frac{F}{k}$$
$$x_d=\frac{f}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}$$
これらの比率が増幅倍率なので、増幅倍率は
$$\frac{x_d}{x_{st}}=\frac{f}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}\frac{k}{F}$$
ここで\(f=\frac{F}{m}\)なので、
$$\frac{x_d}{x_{st}}=\frac{1}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}\frac{k}{m}$$
動的荷重の例②衝撃
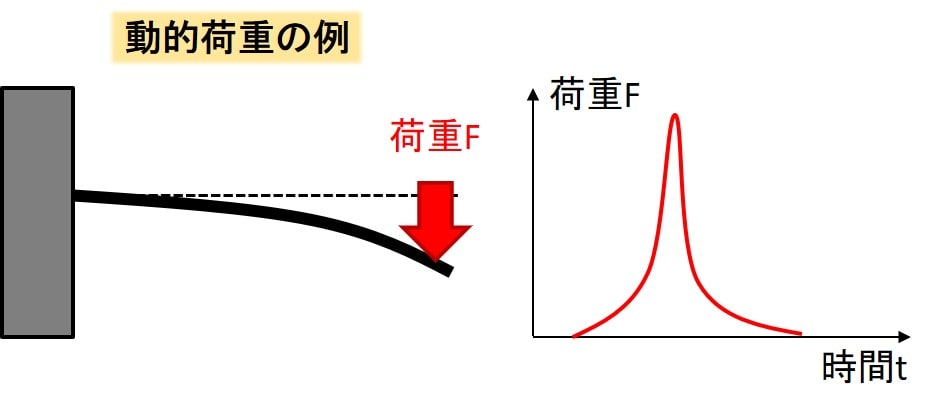
この図のように片持ち梁に衝撃的な力を与えた場合も、 荷重が時間的に変化しますので、動的荷重となります。
こちらも振動工学や機械工学で取り扱うことが多いです。
詳細は今後記事にする予定です。
まとめ
静的、動的荷重の違いについて解説しました。
時間的に荷重の大きさが変化しないもの静的荷重と呼び、 時間的に荷重の大きさが変化するものを動的荷重と呼びます。
動的荷重で取り扱う例として、振動や衝撃がある、ということと、 振動の場合、共振という現象が重要であることを紹介しました。
共振の振幅倍率を、静的荷重の場合の大きさを基準として、 増幅倍率という形で示すことができるということが重要です。
静的、動的の意味をしっかりと理解し、どのような荷重がかかっているかをイメージできるようにすると、 共振の現象の理解も深まりますので、違いをしっかりと区別できるようにしておきましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
