物理勉強してたら微分方程式がいっぱい出てきたんだけど、わけわかんない!


大学レベルの物理は微分方程式がたくさん出てくるからねぇ。避けては通れない数学だから、基礎からきっちり解説するね。
本記事では微分方程式の基礎について解説します。
大学で初めて習って『なんじゃこりゃ??』って思った人も多いのではないでしょうか?
初心者向けにわかりやすく解説します。
本記事をおススメする人
- 微分方程式アレルギーの人
- 1から微分方程式の勉強をしたい人
微分方程式を学び始めた方向けのおススメの教科書・参考書はこちら。
微分方程式にはいろいろ種類があり、名前の付け方について動画で解説していますので、参考にしてください。
微分方程式と普通の方程式の違い
微分方程式は、 そもそも普通の方程式と求める解が違います。
微分方程式と普通の方程式との違い
- 微分方程式:解となる関数を見つける方程式
- 普通の方程式:解となる数字を見つける方程式
微分方程式の例として、下記をあげてみます。
$$\frac{dy}{dx} = y $$
この式を満たす、 関数のyを求めるのが微分方程式です。
一方で普通の方程式の例として、
$$x^2-2x+1 = 0$$
この方程式の解は、数字で求まりますね?
解は因数分解すると\((x-1)^2 =0\) なので\(x=1\)です。
これが微分方程式と普通の方程式の違いです。
微分方程式の解き方
$$\frac{dy}{dx} = y $$
この式を解く前に、微分方程式には解が2種類ありますので、それを説明します。
そのあとに実際に解いてみましょう。
微分方程式の解の種類
よく微分方程式の解を求めるにあたって、下記の2種類の解を使い分けます。
微分方程式と普通の方程式との違い
- 一般解:初期条件なしの解
- 特殊解 (特解):とある初期条件を設定したときの解
どういうこと?って感じた人もいらっしゃると思いますので、例の微分方程式を解きます。
$$\frac{dy}{dx} = y $$
これを満たす\(y\)ですが、勘が良い人はわかるかもしれません。
\(y\)を\(x\)で微分したら\(y\)になる関数、つまり、微分してもな~んにも変わらない関数です。
答えは\(y=e^x\)です!
と、答えたあなた。これは特殊解です。
\(y=2e^x\)も\(y=5e^x\)も\(y=100e^x\)も微分したら元の式になりますね?
なので、とある定数を\(C\)とすると、
$$y=Ce^x$$
これが一般解です。
一般解は、定数Cが含まれた関数で書かれます。
なので、この微分方程式を満たす関数\(y\)は\(C\)の数だけ関数があるんですね。
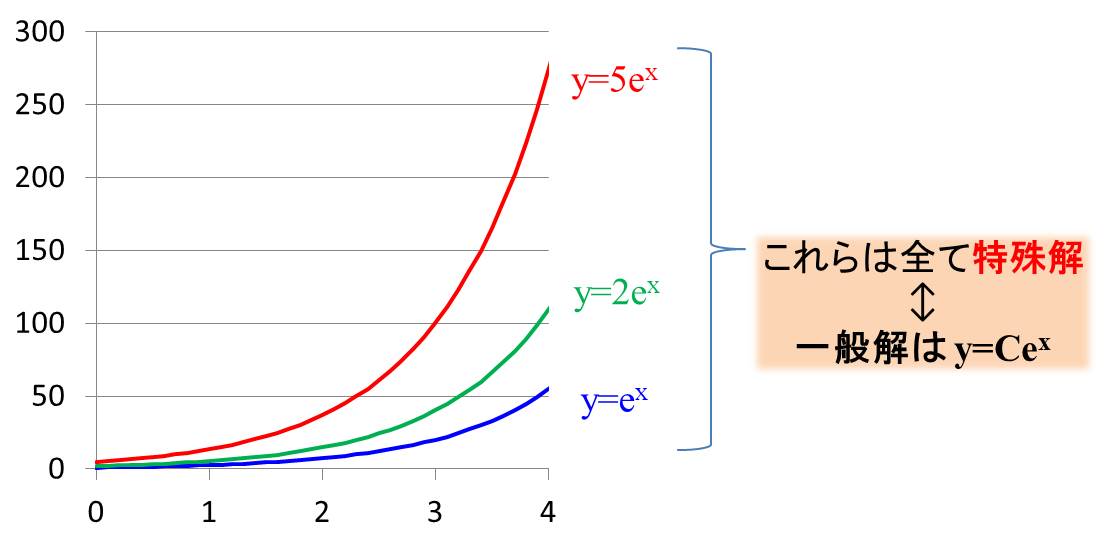
さきほど、\(y=e^x\)は特殊解だ!と書きましたが、これは一般解で\(C=1\)のときの解ですね。
初期条件としては、\(x=0\)のとき、\(y=1\)という初期条件を与えると、
$$1 = C e^0$$
\(e^0\)なので\(C=1\)です。
超基礎-よく使う微分
数学とはいえ、覚えることは多少あります。
微分方程式の最初のステップとして、少なくともこれら3パターンは必ず覚えましょう。
覚えるべき基礎的な微分方程式の形
- $$\frac{dy}{dx} = nx^{n-1} →y=x^n+C$$
- $$\frac{dy}{dx} =y →y =Ce^x$$
- $$\frac{d^2y}{dx^2} =-y →y=C_1sinx+C_2cosx$$
矢印の右側は一般解を示しています。
\(C、C_1、C_2\)は積分定数です。
ではそれぞれ見ていきます。
①\(\frac{dy}{dx} = nx^{n-1}\)
これは右辺がxの式になっています。
これを満たす関数\(y\)を求めるために、右辺を\(x\)で積分します。
$$x^n +C$$
\(C\)は積分定数です。
微分の逆の計算である積分をする、ということで微分方程式を解くことができるものもあります。
②\(\frac{dy}{dx} =y\)
これは先ほど例でやりましたね。
一般解は\(y=Ce^x\)です。
微分しても変わらない関数は\(e^x\)だ!と覚えておいてください。
③\(\frac{d^2y}{dx^2} =-y\)
これもよく出てきます。
2回微分すると、符号が変わって元通りになる関数です。
答えは三角関数である\(sin,cos\)ですね。
\(y=sinx\)を微分すると、\(y'=cosx\)、さらに微分すると\(y''=-sinx =-y\)です。
ちなみに上記は特殊解ですので、一般解にするためには、先ほどの\(e^x\)と同じく、係数に\(C\)をつけて、\(y=Csinx\)となります。
ちなみにこれでもまだ特殊解のレベルです。
\(y=sin(x-δ)\)のように、位相差があるような場合でも成り立ちますね?
ということで、一般解は、
$$y=Csin(x-δ)$$
あれ?でも\(cos\)だって解となりうるんじゃないの??
そう、cosでもいいんです。
なので、この形の一般解を書くとき、下記のように書く場合も多いです。
$$y=C_1sinx+C_2cosx$$
ちなみに、この一般解は\(y=Csin(x+δ)\)と示している内容としては同じです。
三角関数の合成をしてみればわかります。
三角関数の合成公式
$$Csinx+Dcosx = \sqrt{C^2+D^2}sin(x-δ)$$
$$tanδ = \frac{C}{D}$$
今回の式に当てはめると下記のようになりますね。
ここで、\(C =\sqrt{C_1^2+C_2^2}\)とすると、先ほどの一般解は同じことを示していることがわかりますね。
まとめ
今回はここまでで、微分方程式の基本を解説しました。
まとめ
- 微分方程式とは方程式を満たす関数を求めるもの
- 解には一般解と特殊解がある
- 一般解は定数を含み、特殊解は初期条件などで、定数が決まった解
- まず覚えるべき3つのパターンはxのn次関数、指数関数、三角関数
これらは微分方程式の基礎の基礎です。
解くにあたってこれからどんどん難しくなりますので、しっかり理解してくださいね。
次回は変数分離形の微分方程式の解説をしますので、下記リンクをご覧ください。
微分方程式の基礎②-変数分離形-微分方程式の解法について解説
微分方程式を学び始めた方向けのおススメ参考書・教科書はこちら
