[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]なんか振動の勉強してたらグルグルまわっている図が出てきたんだけど、これって何？[/voice]
[voice icon="https://deltapower.site/wp-content/uploads/2020/09/にっこり右側.jpg" name="デルタ先生" type="r"]あぁ、これは相平面というものだね。どのような振動になっているかをいつもと違う見方をしているだけだよ。[/voice]
本日は相平面について説明します。
教科書などでは静止画でしか記述できないので、イメージがつきにくいかもしれません。
本記事ではアニメーションを入れて、イメージがつくように解説します。
[box class="green_box" title="本記事をおススメする人"]
- 振動の相平面についてイメージがつかめていない人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
[/box]
動画でも解説していますので、そちらも是非参考にしていただければと思います。
相平面とは
簡単に言うと、 横軸を変位、縦軸を速さとして、振動を表現したもの、になります。
図としては下記のようなもので、振動の勉強をしている方は教科書などで見たことがあるかもしれません。
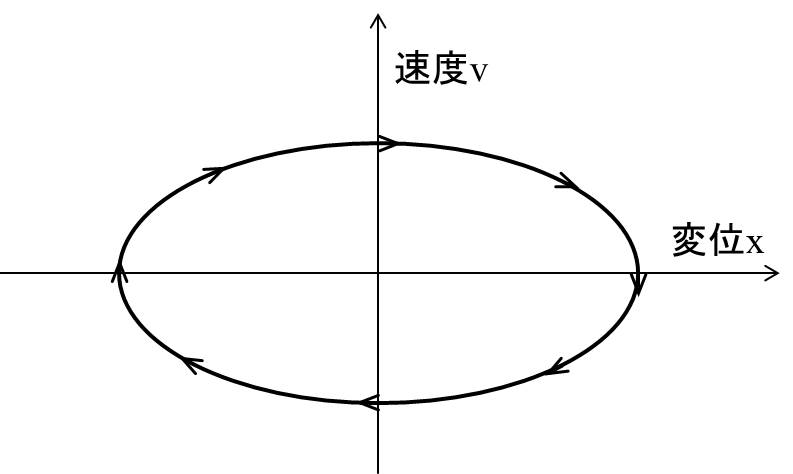
矢印のある線を『 軌道』と言います。
この相平面は減衰のない自由振動の場合を示しています。
注意すべき点は、 時間軸の概念がない、という点です。
単振動の場合
では、なぜ減衰のない自由振動の場合、このようになるかについて説明します。
バネにつながれたモデルの単振動の式は、下記のようになりますね。
$$m\ddot{x}=-kx$$
単振動については、過去の記事を参考にしていただければと思います。
[box class="blue_box" title="参考記事"]
[/box]
$ω_0 = \sqrt{\frac{k}{m}}$とすると、下記のようになりますね。
$$\ddot{x}=-ω_0^2x$$
この一般解から、変位$x$と速度$v=\dot{x}$は、振幅をA、位相δとすると、
②の両辺をω_0で割って、２乗し、①の２乗との和をとると、
整理すると
この③式は高校数学で学んだ楕円の方程式ですね。
軸の長さが$A$と$Aω_0$の楕円を示します。
冒頭の相平面の図になるわけですね。
ただ、時間軸がなく、軌道のみを示すのが相平面ですので、イメージが付きにくいかもしれません。
ということで、相平面上をどのように動くのかをアニメーションで示します。
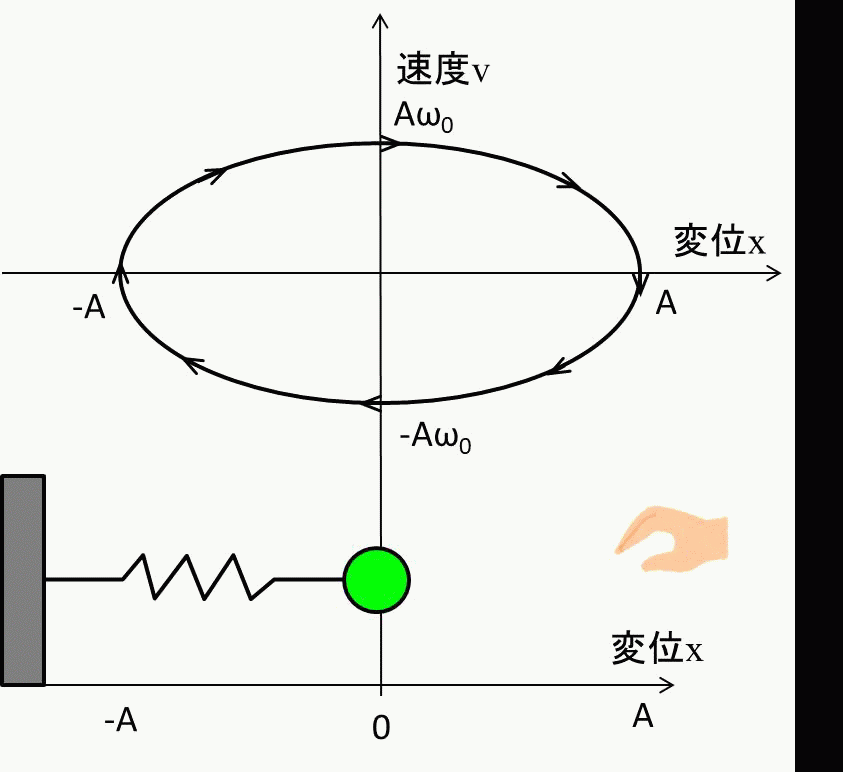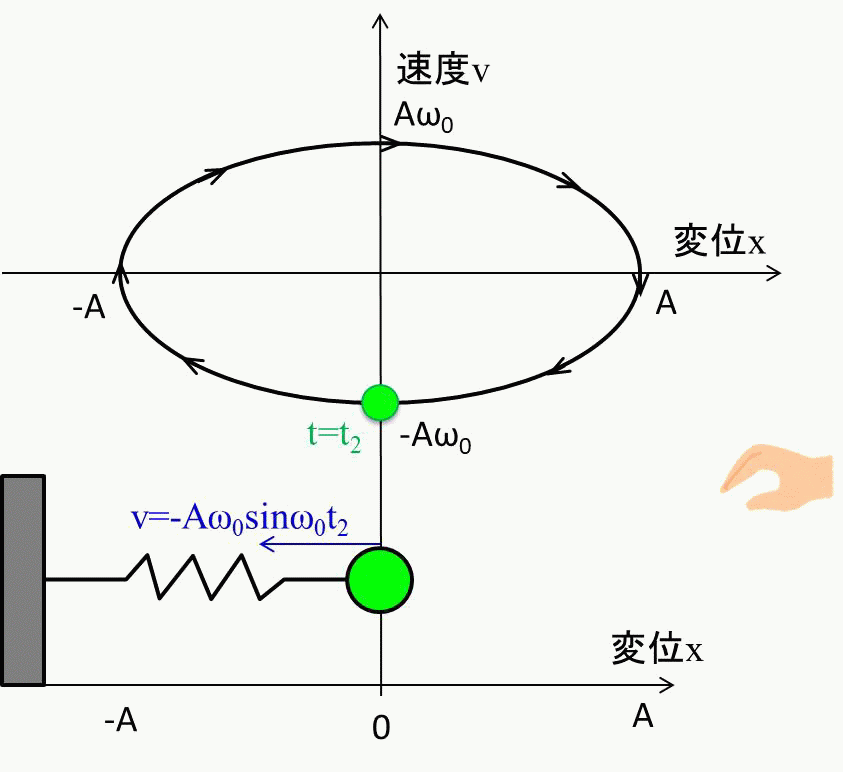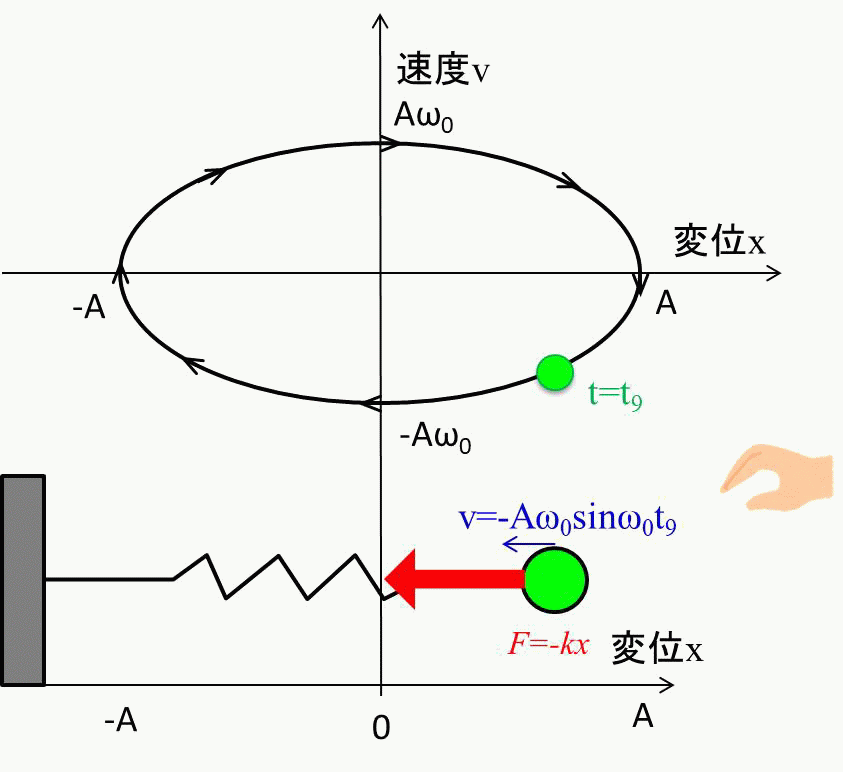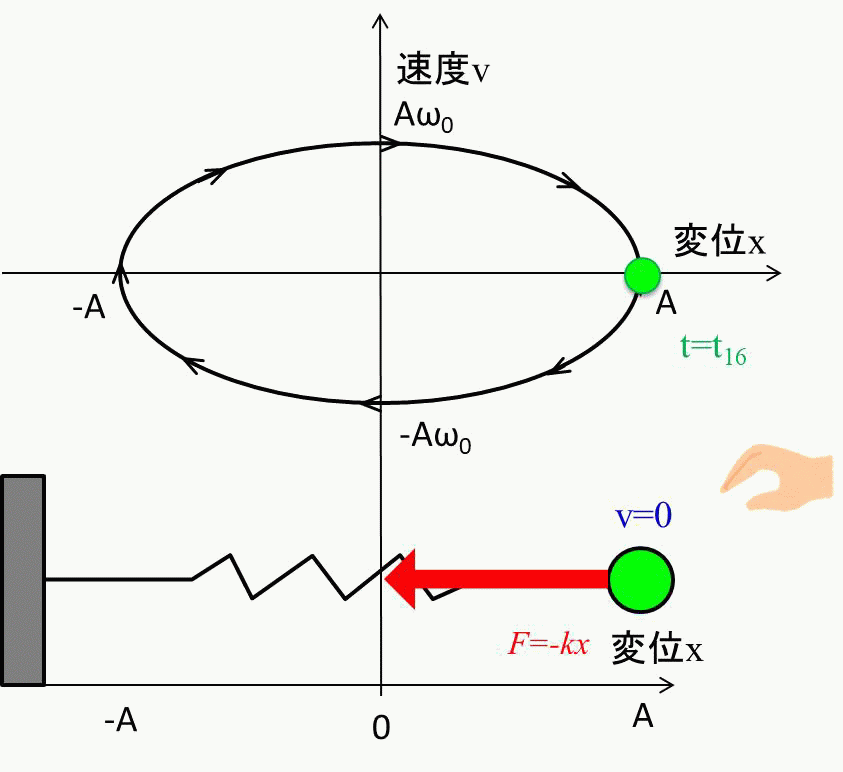
前提条件ですが、バネの自然長の位置をx=0とし、Aの距離までバネを引っ張ります。
t=0の点で手を放し、振動を開始させます。この時の変位と速度は$x=A$、$v=0$です。
ちなみにこの楕円の大きさは、どれだけ最初にバネを引っ張るか、つまりAの大きさで決まります。
さらに、周期Tは$T=\frac{2π}{ω_0}$なので、Aの大きさに寄らないことになります。
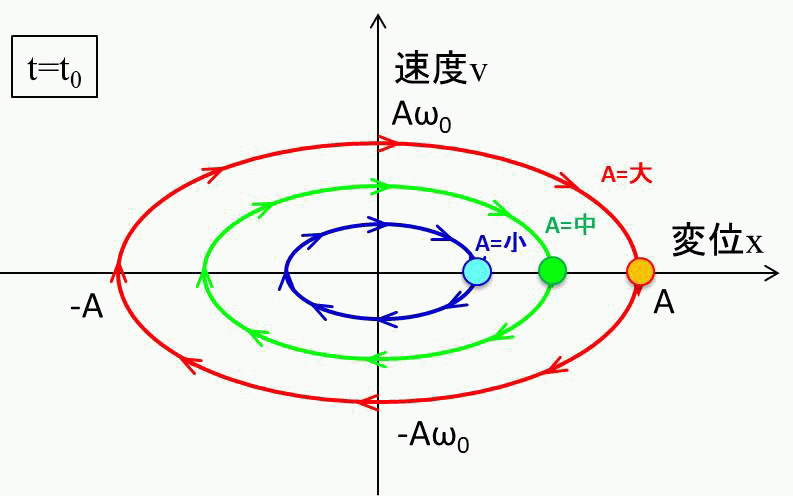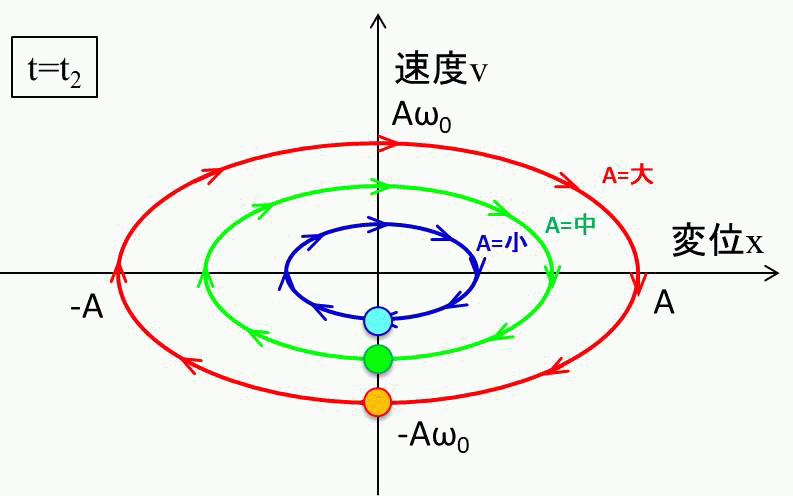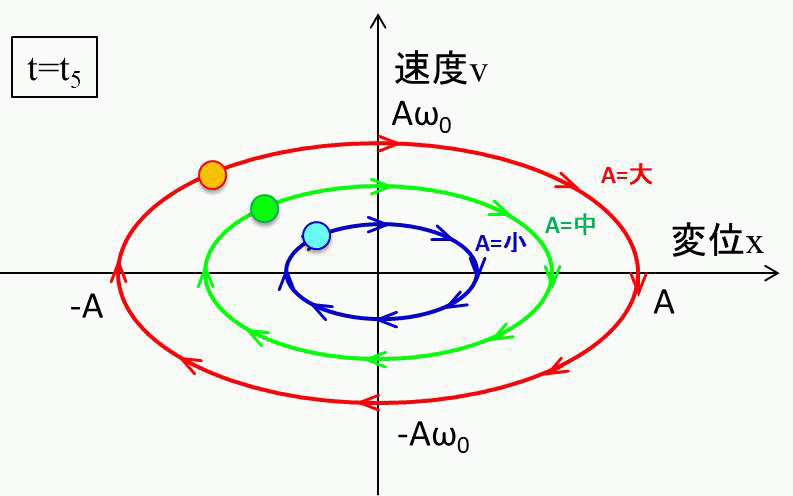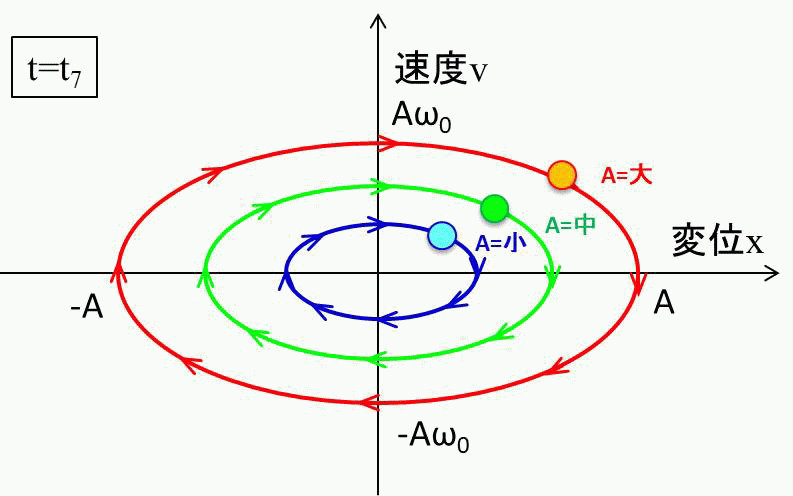
また硬いバネをつかうと$ω_0$が大きくなるので、縦長の楕円になっていきますね。
質量mも$ω_0$に効いてきます。mが小さいと$ω_0$は大きくなるので、質量が小さいとこれも縦長の楕円になります。
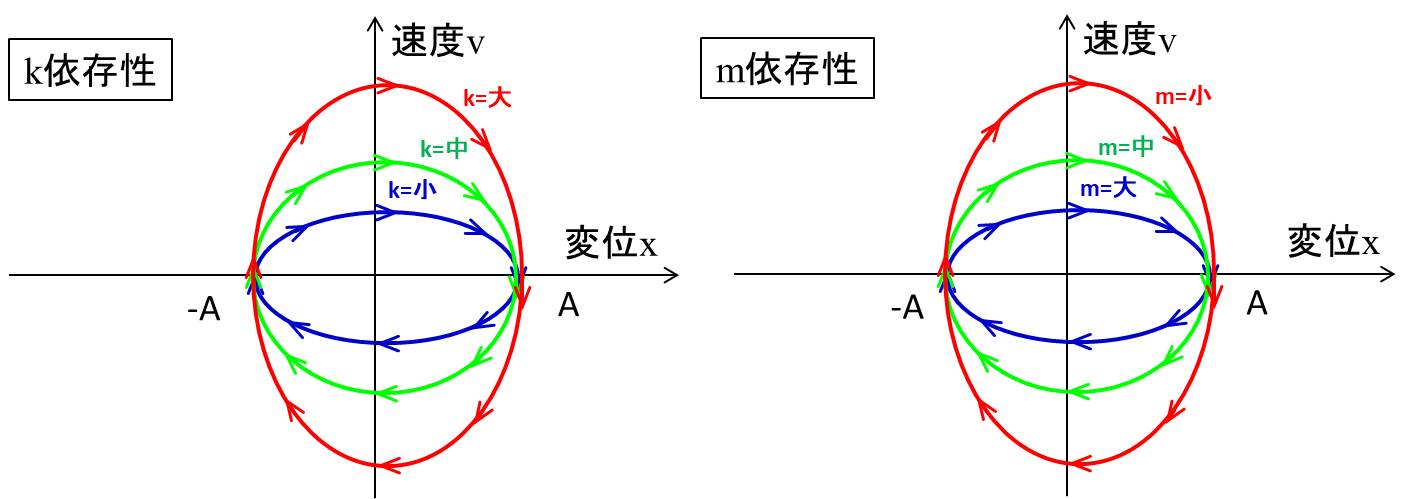
さて、バネ定数kや質量mが変化すると、軌道上の動きはどうなるのでしょうか？
答えは周期$T=\frac{2π}{ω_0}$で、$ω_0 =\sqrt{\frac{k}{m}}$なので、動くスピードが変わります。
硬いバネはすごいスピードで振動しそうですよね？
重たいおもりだと、ノロノロと振動しそうですよね？
このようなイメージをもって、$ω_0$によって相平面での動きが、どのように変わるかをアニメーションで見てみましょう。
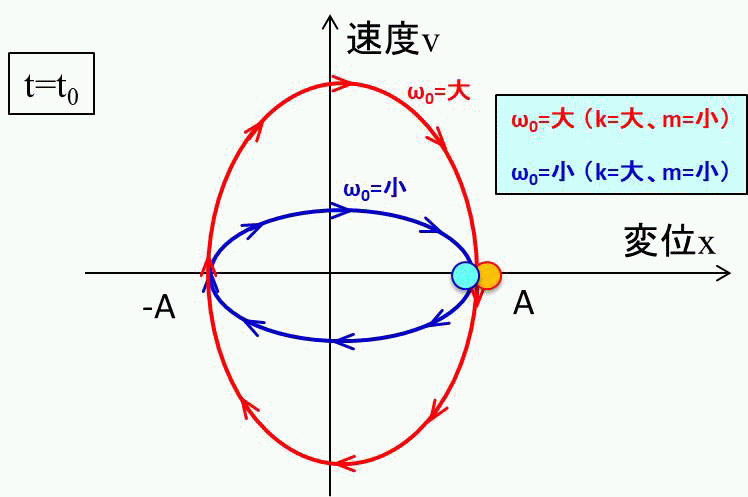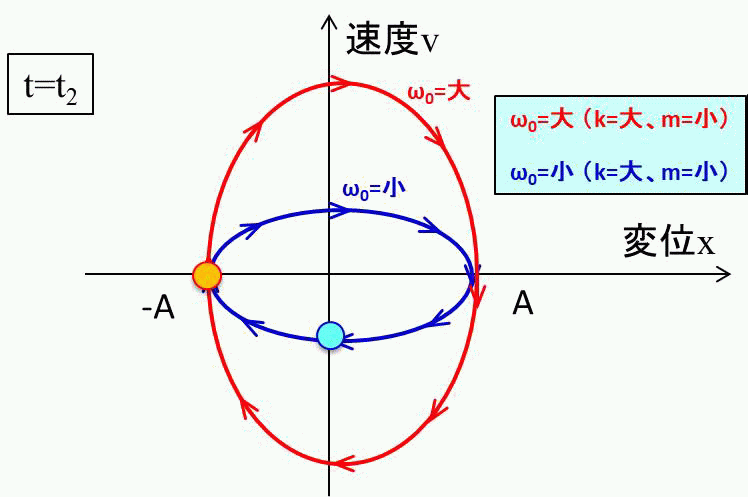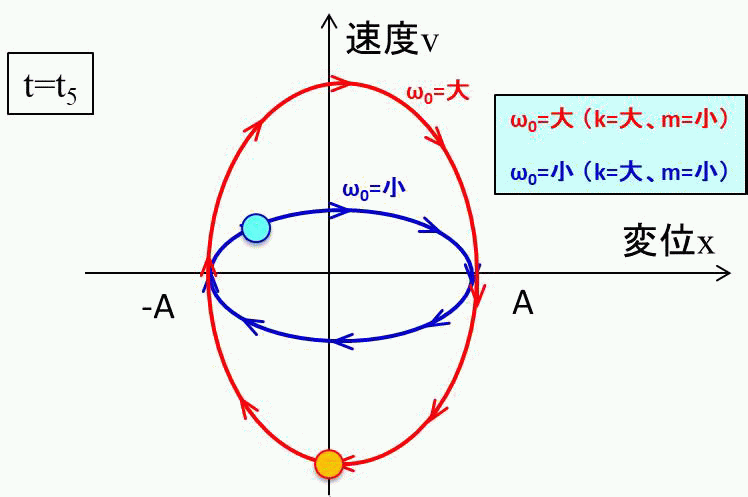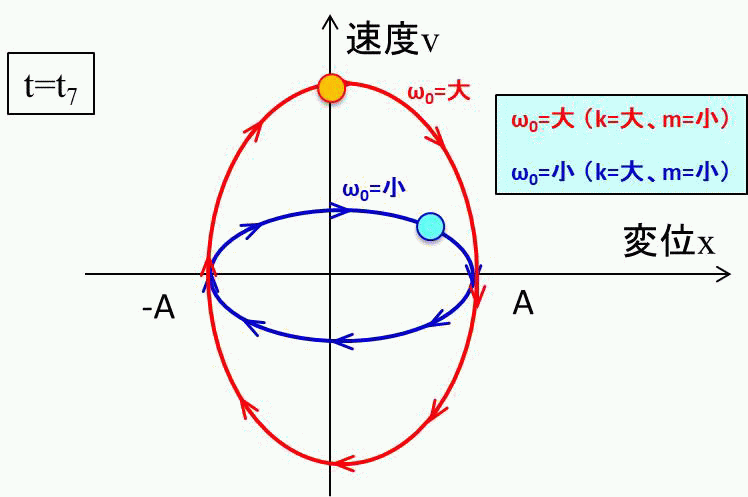
こんな感じ。縦長の円の方が$ω_0$が大きいので、速くなりますね。
相平面をどのような場面で使うか
[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]相平面はわかったけど、こんなのどこで使うの？[/voice]
[voice icon="https://deltapower.site/wp-content/uploads/2020/09/にっこり右側.jpg" name="デルタ先生" type="r"]これは非線形の分野の現象を表現するときに、よく使われるんだ。[/voice]
本記事では線形の現象で最も簡単な単振動のレベルの解説なので、詳細を説明することはできません。
しかし、非線形でのリミットサイクルや分岐現象を視覚的に見る際に、この相平面が役に立ちます。
今後の記事で相平面について、ここまでレベルを上げていきたいと思いますので是非ご覧ください。
Upしたら下記にリンクを貼っていきます。
そもそも非線形の振動って何？？という方は下記の記事を参考にしてください。
[box class="blue_box" title="参考記事"]
[/box]
まとめ
今回は単振動の相平面を説明してきました。
振幅やバネ定数、質量によって、それぞれ相平面の形が変わることが理解できたと思います。
単振動という振動の中で一番単純な内容なので、今後もう少し複雑な振動の場合どうなるかについて解説する予定ですので、楽しみにしてください。
[box class="blue_box" title="参考記事"]
振動・波動の基礎 ⑥相平面について-減衰振動の場合 等傾線法
[/box]
参考文献
- 機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 非線形力学（共立物理学講座6）：戸田盛和、渡辺慎介、共立出版株式会社
- 構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。