微分方程式の種類がいっぱいありすぎてよくわからないよ!


名前の付け方を知っていないと混乱するよね。今日は微分方程式の名前の付け方を学習しよう。
今日は微分方程式の名前の付け方について解説します。
漢字の羅列が出てきて吐き気を催した人もおられるのではないでしょうか?
私は涙目になったことがあります。。
初心者でもわかるように丁寧に解説しますので、最後までがんばりましょう!
本記事をおススメする人
- 微分方程式アレルギーの人
- 1から微分方程式の勉強をしたい人
- 微分方程式の名前の付け方を知りたい人
物理の単振動の運動方程式をベースにした解説動画を公開していますので、そちらもぜひ参考にしていただければと思います。
微分方程式の名前の付け方
微分方程式の例
今回は微分方程式の例を先に示します。
その微分方程式の名は、
定数係数2階同次線形常微分方程式
上記のように今回解説するのは、人の名前がついているような微分方程式ではなく、ある程度ルールがあるものについてまとめて解説しますね。
この微分方程式ですが、物理の運動方程式でもよく出てくる微分方程式で、単振動や減衰振動の運動方程式も該当します。
分け方
定数係数2階同次線形常微分方程式
この微分方程式の名前の分類ですが、5つのパートに分かれます。

それでは、この5つのポイントについて、下記で解説していきます。
階数
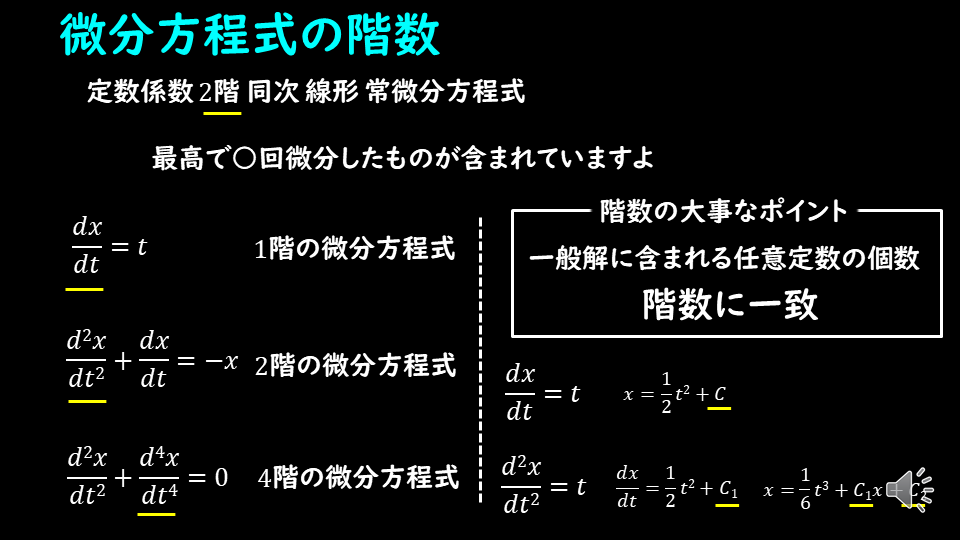
微分方程式の階数ですが、最大で何回微分したかを示しています。
図の点線左側に例を示しており、それぞれの微分方程式で微分の回数が一番多い項に黄色の下線を引いています。
この階数の大事なポイントですが、微分方程式の一般解に含まれる任意定数の個数が階数に一致します。
これは方程式中で微分の回数が一番多い項を、\(x\)の式(微分がついていない式)に戻すには、階数の分だけ不定積分する必要があるためです。
図の点線右側はその例を示しており、黄色の下線は不定積分によって現れた積分定数(任意定数)を示しています。
1階の微分方程式であれば、不定積分を1回する必要があるので、任意定数は1つに、
2階の微分方程式であれば、不定積分を2回する必要があるので、任意定数は2つになります。
同次・非同次

同次、非同次ですが、求める関数にかかわる項をすべて左辺に移項した際、右辺がゼロかどうかで、同次、非同次という分け方をします。
また、人によっては同次のことを斉次、非同次のことを非斉次と言ったりしますので、全く同じ意味として認識しておいてください。
線形・非線形

線形、非線形の微分方程式についてです。
求める関数について、1次の和のみで構成されている微分方程式を線形微分方程式といいます。
1次の和以外の項がある場合、例えば\(x^2\)や\(x\frac{dx}{dt}\)などが含まれると非線形の微分方程式となります。
非線形の微分方程式は解くことがとても難しくなります。
初心者の方は、まずは線形の微分方程式を解けるようにしましょう。
常微分・偏微分

常微分、偏微分についてですが、
常微分は1変数関数の微分のみで構成されている方程式を常微分方程式といいます。
また、多変数関数の微分が含まれる場合は偏微分方程式といいます。
微分には偏微分と全微分の2種類があり、常微分の場合は偏微分と全微分が全く同じなので、
普通は全微分の\(\frac{dx}{dt}\)という形式で表します。
一方、多変数関数の場合、偏微分と全微分が示す意味がそれぞれ異なっております。
しかし、全微分であろうが、多変数関数の場合、偏微分が必ず含まれる形になりますので、
多変数関数の微分方程式は偏微分方程式になります。
定数係数

最後に定数係数の意味を解説します。
2階同次線形常微分方程式は図に示されているような、\(P(t)\)や\(Q(t)\)を含んだ形で一般的に表されます。
この係数\(P(t)、Q(t)\)が定数の場合、定数係数の微分方程式といいます。
物理でも単振動や減衰振動の運動方程式は定数係数の微分方程式に分類されます。
定数係数でない場合の微分方程式は、解くことが非常に難しくなります。
振動工学との関連性
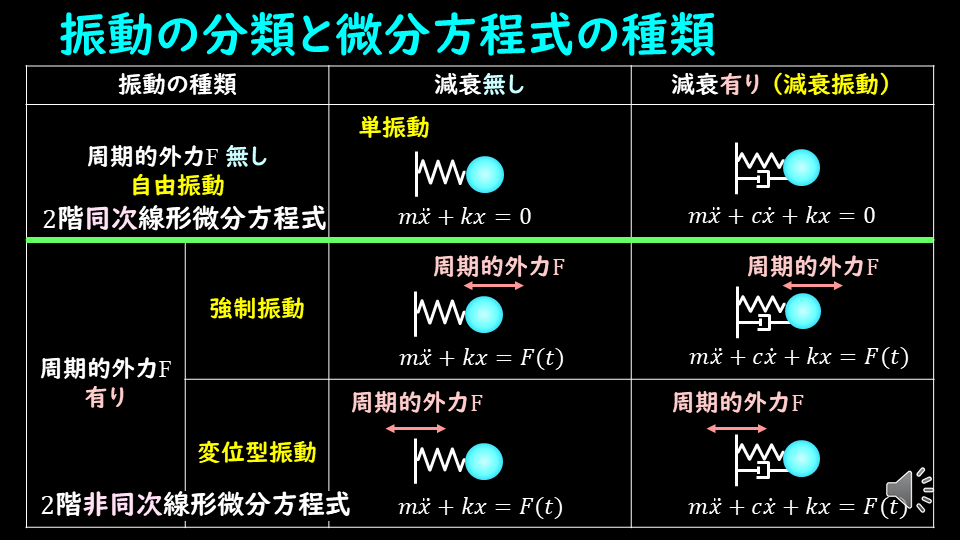
振動工学で習う振動の分類と、微分方程式の種類を表で示しています。
図の緑線の上下で、2階同次線形微分方程式、あるいは2階非同次線形微分方程式とわかれます。
周期的外力が作用するかどうかで同次、非同次が決まるわけですね。
なお、振動工学の全体像の講義や、過去記事を参考にしていただければ、さらに理解が深まると思います。
まとめ

微分方程式の名前の付け方、分類について解説しました。
ルールさえ理解しておけば、あとは解き方をしっかりと理解するだけですので、まずは名前の付け方を理解しましょう。
微分方程式の基礎④-階数?同次?線形?常微分?名前の付け方を解説
微分方程式の初心者向けのおススメ教科書・参考書はこちら
