振動工学ってどのようなことを勉強するの?微分方程式ばっかり解いてて、流れがよくわからないよ。


計算が結構多いし、振動工学で勉強する全体像を説明した方がよさそうだね。
本記事では、振動工学でどのようなことを勉強するかについて、全体像がわかるように解説します。
本記事をおススメする人
- 振動工学の全体像を知りたい人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
動画でも解説していますので、下のリンクからぜひご覧ください。
振動工学を勉強する目的
そもそも、振動工学を勉強する目的ですが、ざっくりまとめると下記になります。
振動工学の内容
- 実際のモノがどのように振動するか
- 実際のモノが振動がどのように伝わるか
- 振動の数学的な取り扱い方
上記を理解することで、 構造物の振動を制御 する
最終的にはモノの振動を制御するための設計をどうするか、これができるようにするための学問です。
具体例としては、建物とか橋とかに振動が加わると壊れちゃいますね。
これを抑えるために、どんな構造にしたらいいのかな~と、考えるのに必要なのが振動工学です。
逆に揺らしたい構造にする場合もあります。
ゲームのコントローラーなどは、心地よい振動を与えられるような構造にしています。
マッサージ器とかも、できるだけ少ないエネルギーで振動できるような構造設計になっています。
このように、 自由自在に振動を制御できるようになるために、振動工学が必要なのです。
振動工学を学ぶにあたって目指すところ

社会人の方であれば、振動工学が必要になる方といえば、何かしらモノづくりに携わっている設計者の方が多いのではないでしょうか。
設計するにあたって、最近ではコンピュータの性能も上がり、多少複雑な計算でも高速で計算することができます。
しかし、手軽に計算できる一方、出てきた計算結果については技術者が良否を判断しなければなりません。
振動工学を学ぶことによって、振動について直感的な理解ができるようになれば、計算があっているかどうかの判断もしやすくなります。
そのためには、振動工学でひたすら運動方程式を解いて、振動の状態をしっかりと理解していきましょう。
振動工学の全体像

概要
振動工学の3項目
- どうやって振動を制御するか?
- 振動データを測定、解析する方法
- 波動・音波関連
特に①のどうやって振動を制御するのか、という点を大学の授業などでは重点的に学習します。
これは振動そのものを理解する上でベースとなる知識になるからですね。
最初は1自由度から始まり、自由度を増やして多自由度、最終的には連続体まで学習します。
その後、回転体や自励振動、非線形振動などが応用として学習する範囲になります。
振動のパターン
それぞれの項目で共通して学習する内容として、下記のような振動状態の種類があります。
- 減衰があるか、無いか
- 外力があるか、無いか
- 外力がある場合、物体を直接揺らしているか(強制振動)、土台を揺らしているか(変位振動)
これらのモデルと運動方程式を表にまとめました。
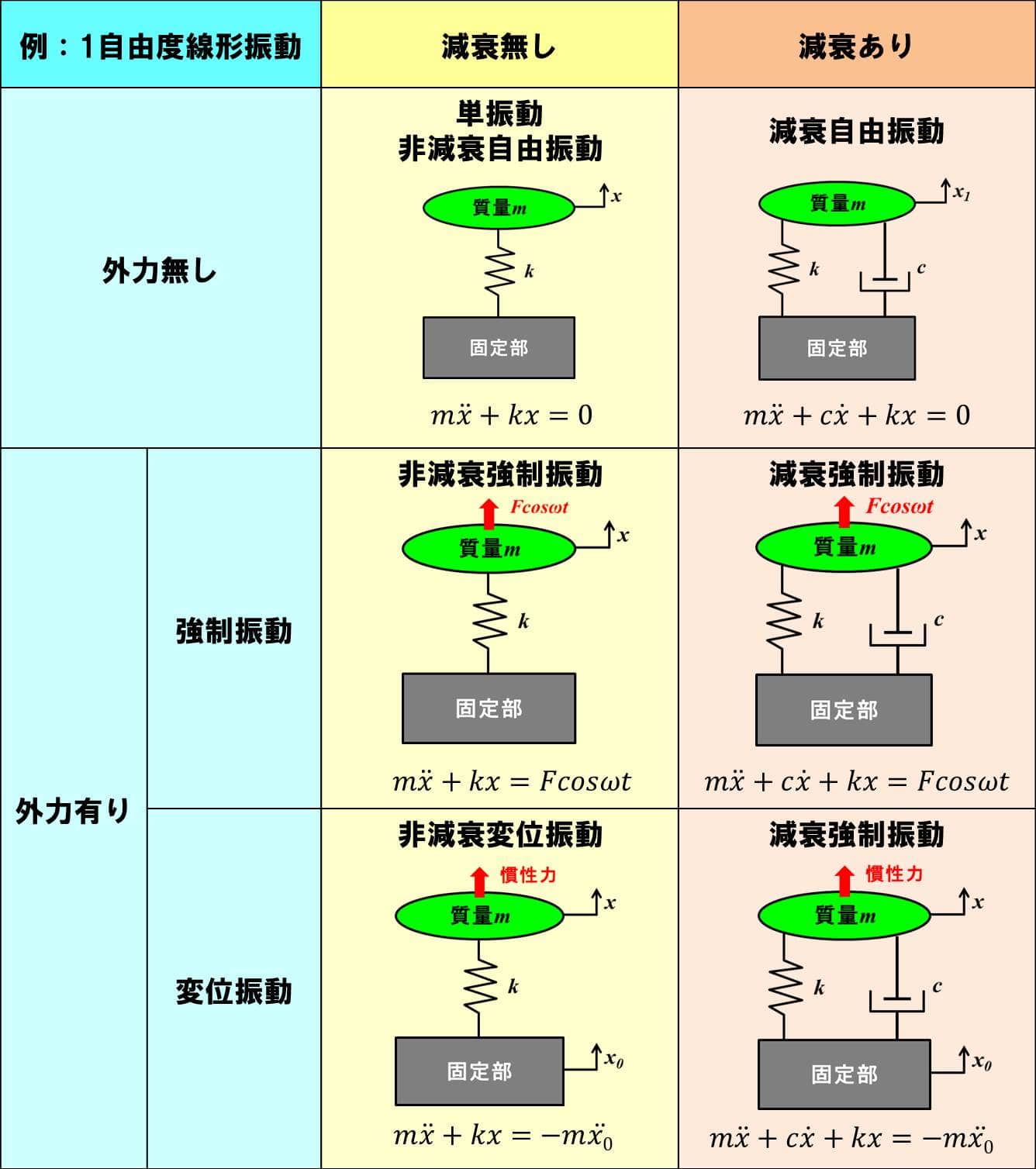
これは1自由度の線形振動の場合で、2自由度系であっても、多自由度系であっても、非線形であっても同じです。
単振動が一番簡単で、減衰ありで外力が加わると、強制振動、あるいは変位振動となり、複雑な計算が必要になります。
これら強制振動、変位振動の場合、振動工学で重要な現象、共振現象を考える必要が出てきます。
共振とは下記のように、ある周波数の周期的外力を与えると、物体が大きく揺れる現象をさします。
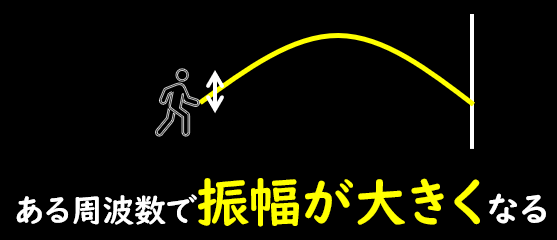
さて、これらは全て1自由度、つまり質点が1つだけ、という状態です。
質点を増やしていくと、実際のモノの状態に近づいていくのですが、増やすとどうなるのか・・・?
下図のようなイメージですね。
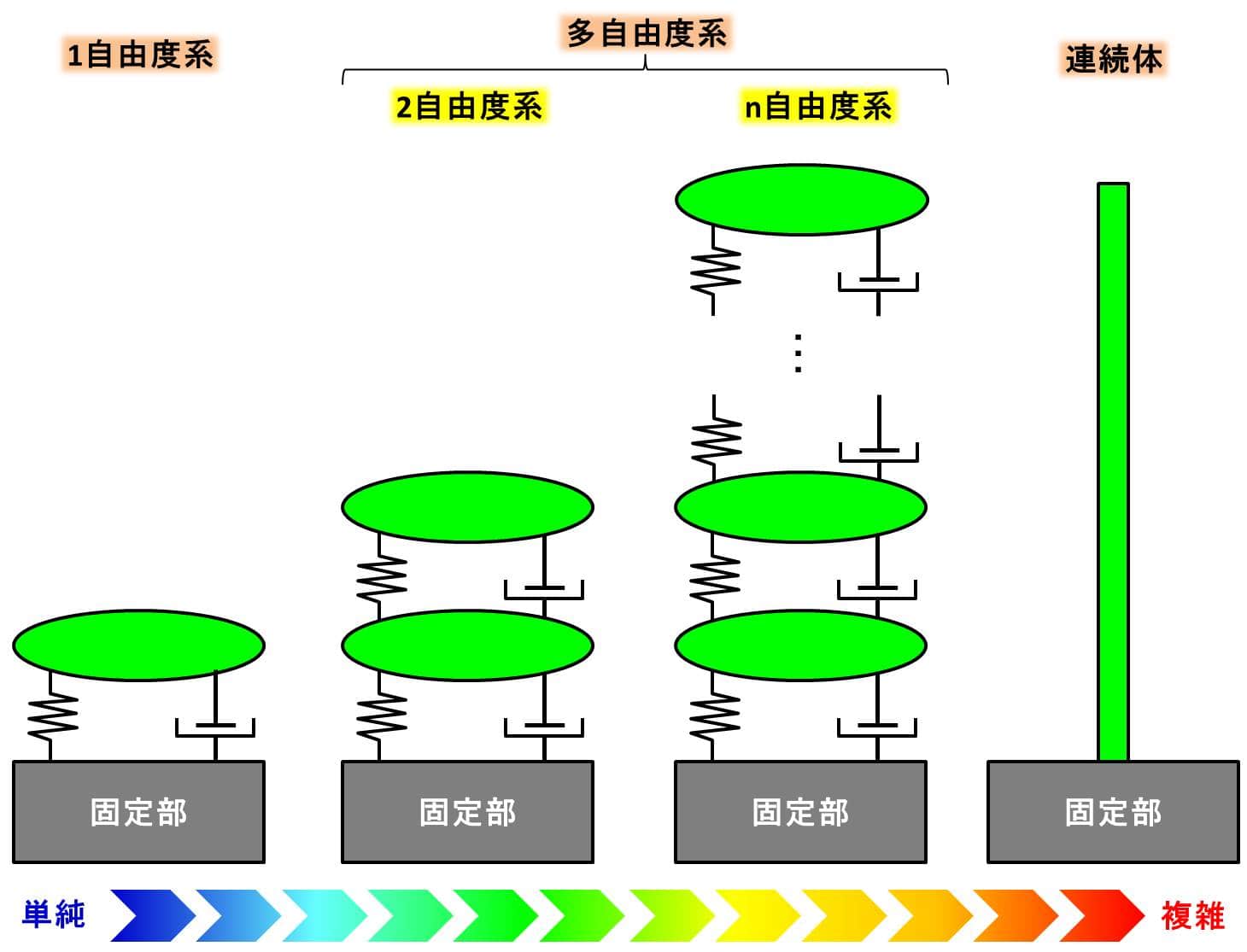
2自由度、多自由度、連続体と実物に近づけると、どうなるか解説した記事は下記となります。
基本的には1自由度系と考え方は同じですが、自由度が増えることで、振動の振動モード(固有モード)というものを考える必要がでてきます。
この 振動モード(固有モード)の考え方は超重要です。
振動モードの例として、下図を見てみましょう。
人が壁につながれたロープを上下に振っている図なのですが、ロープを振る速さを変えると、ロープの形状が変化して共振状態になります。
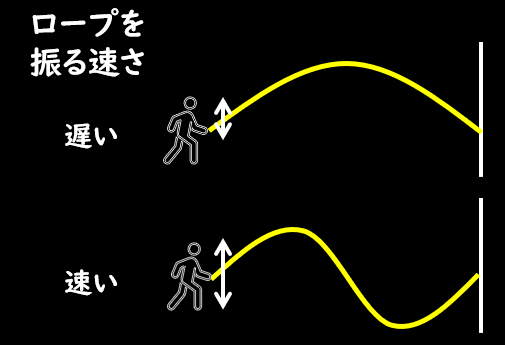
この振動する形状を振動モード(固有モード)と呼びます。
最後に、これまで線形の力が働くような系を考えていましたが、世の中には非線形の力というものが多く存在します。
非線形の力とは、 変位の1次に比例しない力、を指します。
つまり$y=ax$のような1次関数で表現できない力のことになります。
両端固定の梁だったり、ブランコだったり、雲のうずまきだったり・・・
この非線形の力を考えると、より複雑でリアルな現象を理解できます。
これらについては今後、詳細をわかりやすく記事にしていきます。
まとめ

振動工学の基礎的な部分の概要を解説しました。
まずは、単純な1自由度の振動からスタートします。
その中でも減衰のないものを単振動と呼びます。
振動のパターンですが、減衰項の有無、外力を付け加える、もしくは土台を揺らすようなパターンがあります。
基本的には1自由度系の考え方が多自由度系の振動でも応用できますが、固有モードの考え方など、多自由度系ならではのものを理解する必要があります。
そして、非線形の力を考えることで、さらに振動工学の応用範囲は広がります。
これらを学んでいくことで、立派な振動の専門家になれますので、私といっしょにがんばっていきましょう!
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
