減衰の係数って、\(c\)とか\(ζ\)とか色々あってどれを使ったらいいかよくわからないよ。


確かに何種類か表し方があるから、ちゃんと整理して理解しておこうね。
今回は振動の減衰についてのまとめをします。
授業で習った減衰振動、復習しようとしてネットで検索すると
「あれ?表記が習ったものと違う・・・!?」
ということがよくあるのではないでしょうか?
減衰比ζとか減衰率γとかいろんな表記があって、微妙に運動方程式の形も変わってきたりして、
非常にイライラした覚えがあります。
そんなイライラしたことのある方のために、本記事では減衰の表し方や、いろんな減衰の種類について触れて整理していきたいと思います。
減衰係数やら減衰率やらいろんな減衰の表し方がありますので、しっかりと理解して、間違いのないようにしましょう。
そもそも減衰って何??っていう方や、減衰振動の運動方程式を解きたい方は、下記の過去記事を参考にしてくださいね。
振動・波動の基礎②-リアルな振動を考えよう!振動の減衰について詳しく解説
減衰振動における自由振動の計算-過減衰の形と双曲線関数について解説
本記事をおススメする人
- 減衰の表し方の区別がつかない人
- 減衰について整理して学びたい人
動画でも解説していますので、是非参考にしていただければと思います。
振動の減衰の表し方 一覧
最初に一覧表を示します。
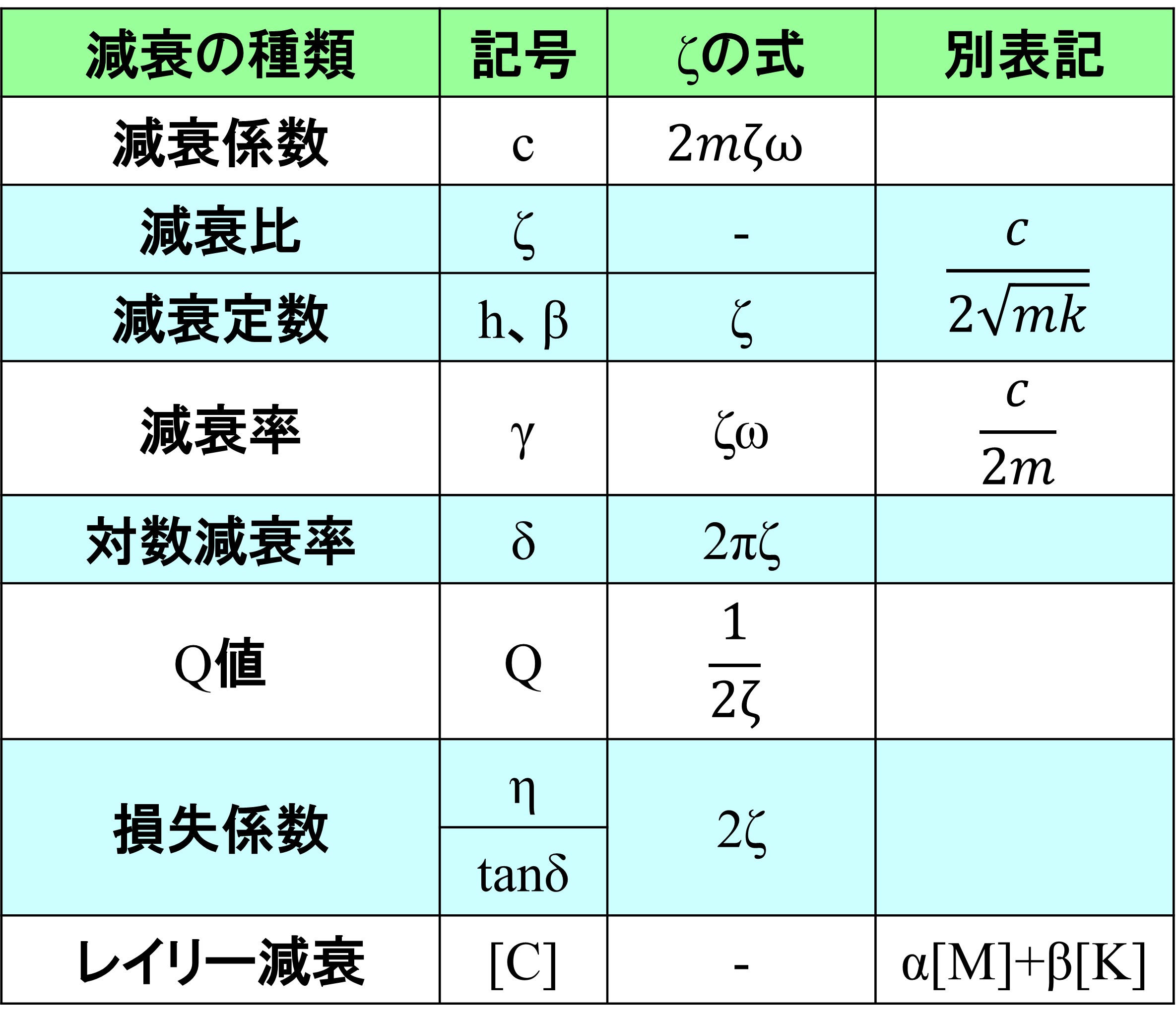
後ほど個別に解説していきますね。
振動の減衰とは
振動の減衰とは、下図のように時間が進むにつれて振幅が小さくなる現象でした。
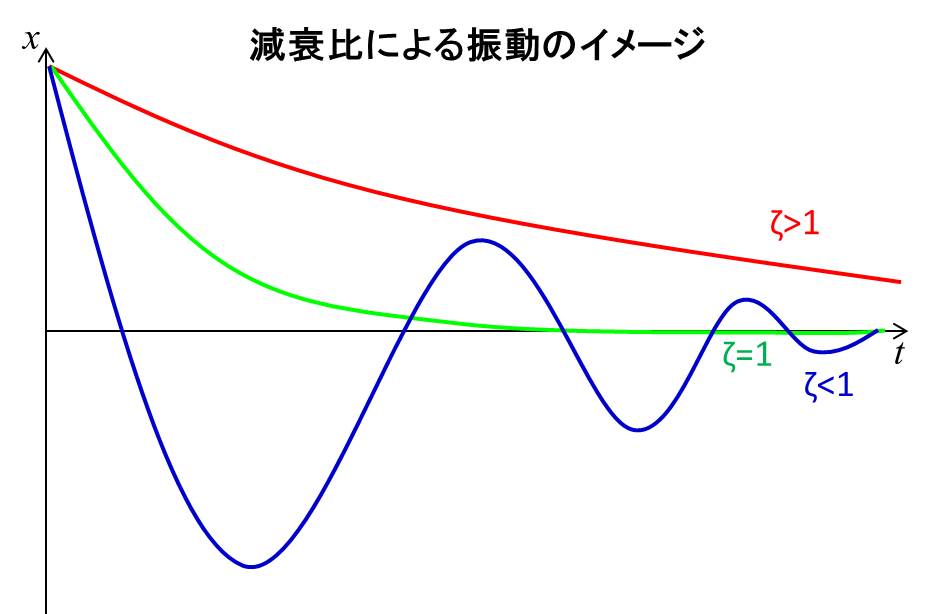
つまり減衰とは、振動を邪魔する成分、というわけです。
\(ζ\)が減衰率を表していてζが1以上の場合、振動しなくなります。
(\(ζ=1\)のときを臨界減衰、\(ζ>1\)のときを過減衰と呼びます。)
さて、この邪魔する成分、どんなものがあるでしょうか?
主なものを下記にまとめてみました。
減衰の種類
- 空気抵抗などの粘性減衰
- 内部摩擦による減衰
- 物質界面の摩擦減衰
このようにいろんな減衰があり、それぞれいろんな減衰の表し方をします。
その中でも一番よく使われるのが、速度に比例する粘性減衰です。
教科書などで扱うもっとも簡単な減衰ありの振動の運動方程式を、実際に見てみると、減衰の項は下の赤字の部分になります。
$$m\ddot{x}\color{red}{+c\dot{x}}\color{black}+kx=0$$
この\(c\dot{x}\)という項は、速度に比例する減衰を示しているわけです。
厳密には粘性減衰のすべての場合が速度の1乗に比例するわけではないのですが、減衰の初歩的な理解のために、このように簡単に1乗で表記しているのですね。
減衰振動については動画でも解説していますので、参考にしていただければと思います。
減衰項の中身
減衰係数c
さて減衰項\(c\dot{x}\)について、もう少し深く見ていきましょう。
まず定義として、減衰項の係数\(c\)ですが、これを減衰係数と呼びます。
もっとも簡単な減衰振動の運動方程式に出てくる減衰項の係数なので、減衰係数です。
減衰比ζ
次によく使うのはこの減衰比ζでしょう。
運動方程式の両辺を\(m\)で割って、固有振動数\(ω\)を用いて書き直すことで、\(ζ\)が出てきます。
$$\ddot{x}+2ζω\dot{x}+ω^2=0$$
$$ω=\sqrt{\frac{k}{m}}$$
この減衰比\(ζ\)と減衰係数\(c\)には下記の関係があります。
$$ζ=\frac{c}{\sqrt{mk}}$$
減衰定数h、β
この減衰定数\(h\)と\(β\)は減衰比\(ζ\)と中身は同じです。
$$h=β=ζ=\frac{c}{2\sqrt{mk}}$$
紛らわしい!!
減衰率γ
これも教科書によっては出てきます。
$$γ=ζω=\frac{c}{2m}$$
\(ζ\)と\(γ\)を使う人が多いのですが、統一してほしいものです・・・
対数減衰率δ
対数減衰率は下記のように求めることができます。
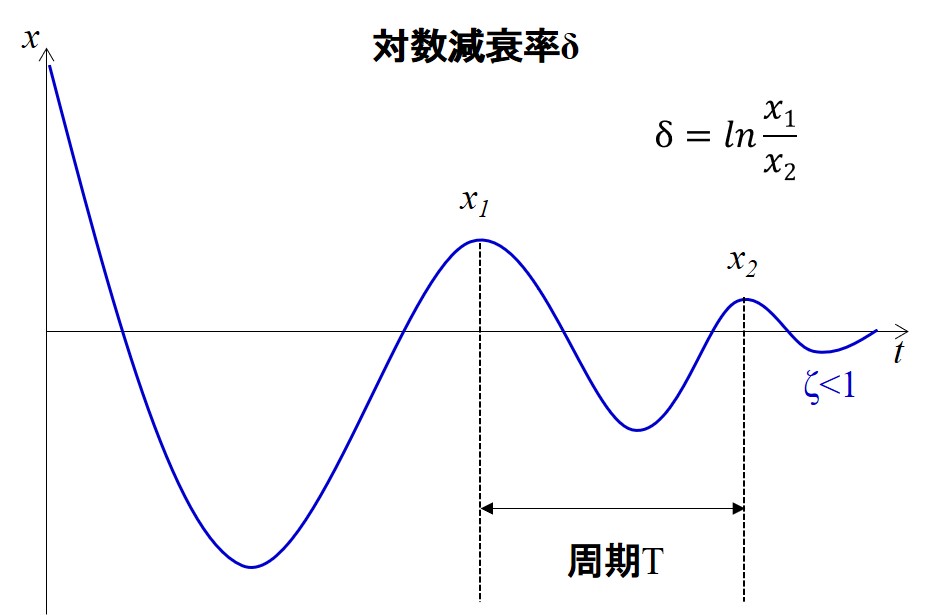
対数減衰率は減衰率ζと下記のような関係があります。
$$δ=2\piζ$$
Q値
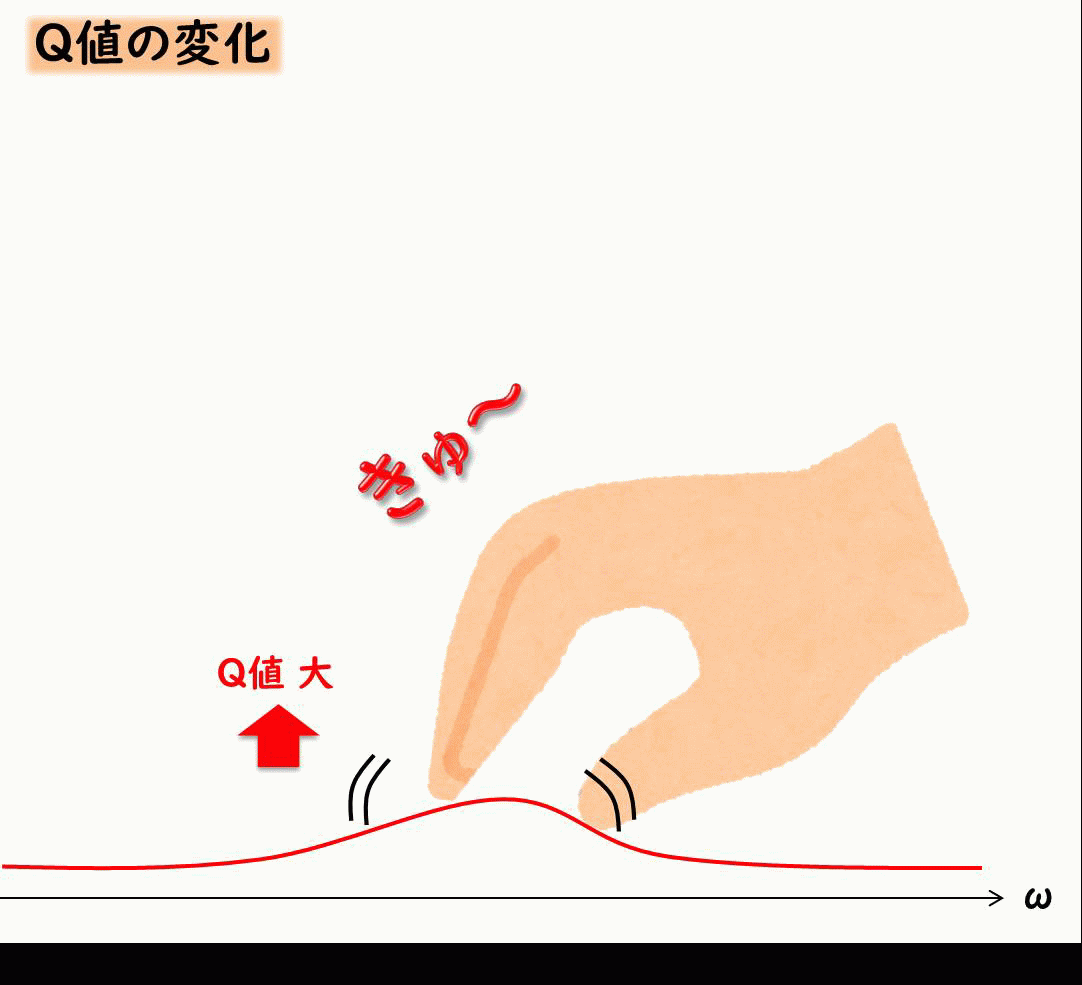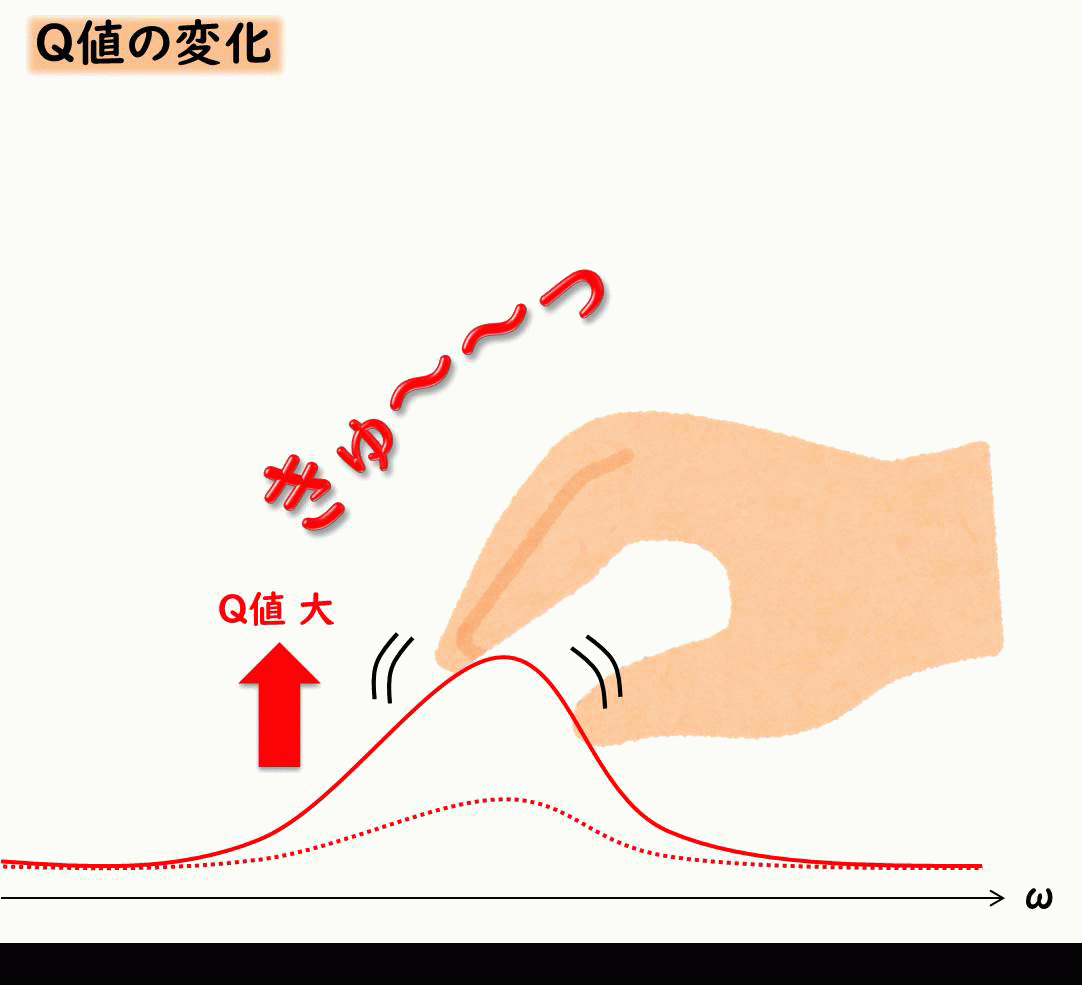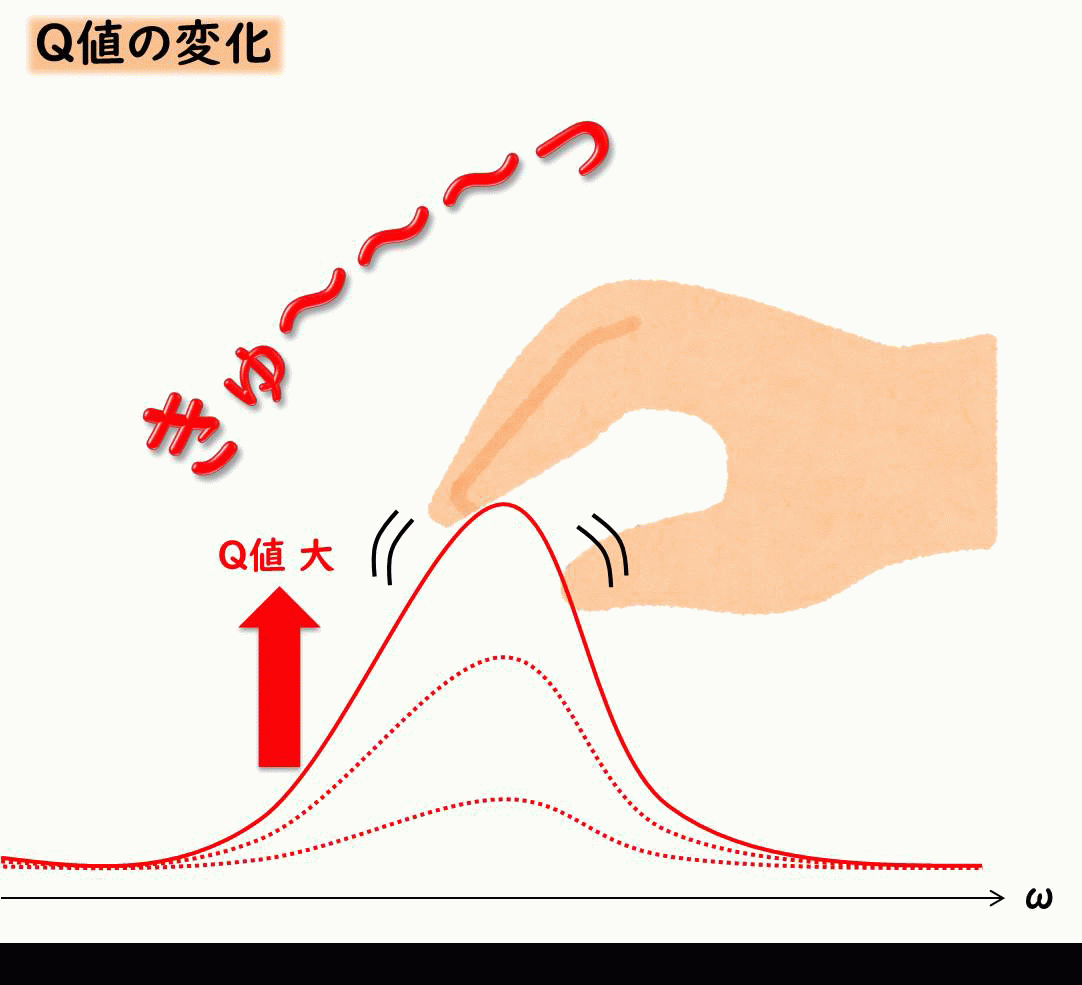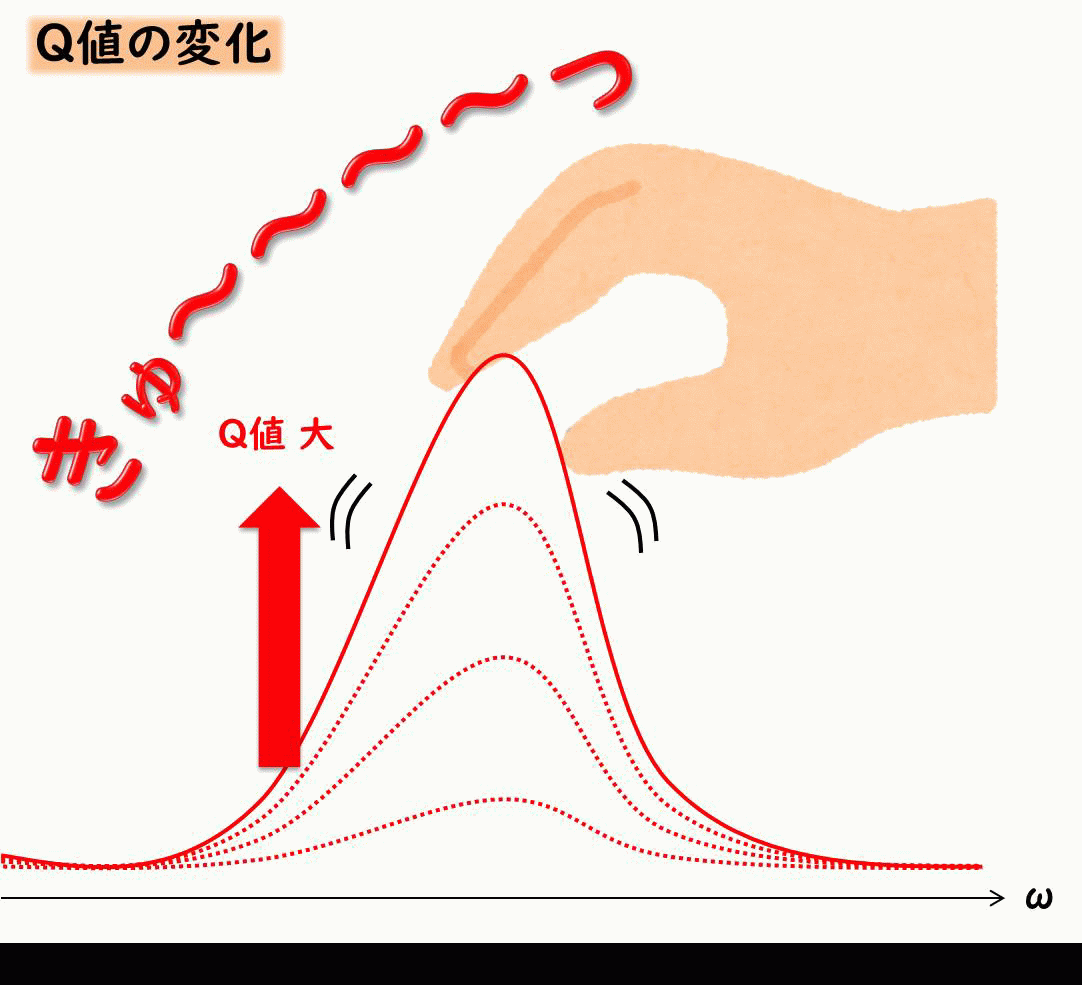
\(Q\)値とは共振の鋭さを示すパラメータでした。(過去記事)
この\(Q\)値には減衰比\(ζ\)と下記のような関係にあります。
$$Q=\frac{1}{2ζ}$$
損失係数\(η\)
\(η\)(イータ)という文字も使われます。
損失係数\(η\)には減衰比\(ζ\)と下記のような関係があります。
$$η=2ζ$$
\(tanδ\)
\(tanδ\)とは、材料の分野では損失係数、電気回路の分野では誘電正接(誘電損失)とも言われます。
振動を抑える材料を制振材料と呼んだりするのですが、どれだけ振動を抑えることができるかの目安として、\(tanδ\)を使います。
\(tanδ\)は\(η\)と同じ意味で、下記のようにイコールでつながれます。
$$tanδ=η$$
損失係数って何?
この損失係数は\(ζ\)などにも変換できるので、減衰を示しています。
でもなぜ\(tan\)??と思った方もいらっしゃると思います。
これは複素数平面で考えると、イメージがつかめると思います。
結論としてイメージを示しておくと、
複素数平面において、虚部(複素数部分)は振動のロスを示していて、
\(tanδ\)は虚部をどれだけ持つかを示しています。
はい、何を言っているのかわかんなーい!と思った方は下記を見てみましょう。
振動を複素数で書くことができるのは過去記事で学びましたが、減衰を加えると振幅は下記のようになります。
$$Z=\frac{F}{-mω^2+k+icω}$$
これを複素数の部分を分子にもってくるために、分母と共益な複素数を分母分子にかけると、
$$Z=\frac{-mω^2+k-icω}{(-mω^2+k)^2+c^2ω^2}F$$
この式を見てみると、減衰がなければ虚部の部分がゼロになりますよね?
減衰がない場合は実部がそのまま振幅になりますが、虚部が存在する、すなわち減衰があると、
振幅は上式の実部に相当するので、減衰の分だけロスします。
複素数平面で考えると、虚部があると斜めになって実軸と角度をもつわけで、実部の長さは短くなるイメージですね。
この実部とのなす角を\(δ\)としていて、傾きを\(tanδ\)としているわけで、当然傾きが大きいと実部の長さが短くなりますよね?
つまり減衰が大きい
⇒\(tanδ\)が大きい
⇒複素数平面で考えると、傾きが大きくなる
⇒実部が小さくなる
⇒振幅が小さくなる
という流れになります。
\(tanδ\)を求めるには?
減衰にはいろんな種類があるのですが、構造による減衰については動的粘弾性測定という測定で求めることができます。
また、電気回路の交流の分野では、電圧と電流の位相のずれによって電力のロスが生じます。
これはコンデンサやコイルが電流や電圧の位相を進めたり遅らせたりする効果があるからで、この位相ずれによるロスを誘電損失と呼び、これも\(tanδ\)で表します。
レイリー減衰
振動分野で計算上、減衰を簡単に扱うための仮定があり、それがレイリー減衰と呼ばれるものになります。
別記事でも解説しておりますので詳細はそちらを参考にしていただければと思います。
下記の動画でも解説していますので、参考にしていただければと思います。
振動を多自由度で扱う場合、計算を簡単にするためにモード座標系に座標変換するのですが、
その座標変換をするために、下記のように減衰マトリックスを仮定します。
$$[C]=α[M]+β[K]$$
モード座標系については過去記事を参考にしてください。
このようにすることで、減衰マトリックスの\(α\)の部分は質量マトリックスへ、\(β\)の部分は剛性マトリックスに押し込むことができ、減衰無しの時と同じように座標変換ができるようになります。
通常、減衰マトリックス[C]は対角行列ではなく、いろんな非対角項が入っているのですが、非対角項の影響は小さいと仮定したのがレイリー減衰です。
レイリー減衰を仮定して計算すると実際の振動をよく再現できるので、振動の設計の分野ではよく使われています。
まとめ
減衰について、最後に表にまとめておきます。
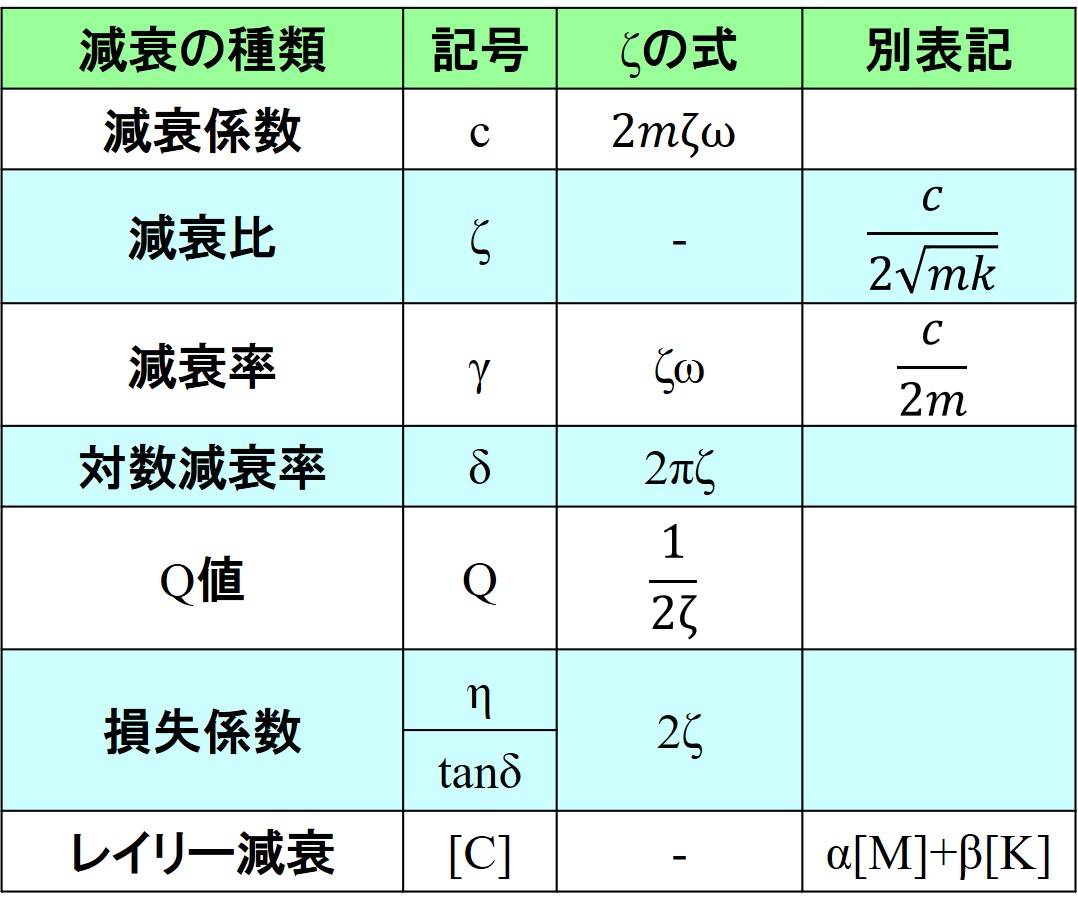
このように減衰にはいろんな種類があります。
正直、表記については一つに統一してくれと思うのですが、今のところ、個別に理解しておくしかないです。
振動を語る上で減衰は非常に大事なパラメータなので、しっかりと意味を理解しておきましょうね。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら