レイリー減衰って出てきたんだけど、これって普通の減衰と何が違うの?


レイリー減衰はモード解析法で使われる減衰の表し方なんだ。今回はレイリー減衰について解説するね。
本記事ではレイリー減衰について解説します。
シミュレーションとか振動解析をやってると、急に横文字の減衰が表れて「なんじゃこりゃ??」って思った人も多いのではないでしょうか?
私も「シミュレーションを行うときにはレイリー減衰を使うんだよ~」と教えられて、はてなのお花畑が頭に浮かんでしまった記憶があります。
端的に行ってしまえば、 モード解析法で減衰振動を取り扱うための減衰なのですが、その中身について、本日は初心者でもわかるように解説しますね。
レイリー減衰を学ぶ前に、前提知識として、モード解析法について過去の記事で解説していますので、そちらを参考にしてください。
下記動画でも解説していますので、是非参考にしていただければと思います。
運動方程式とモデル
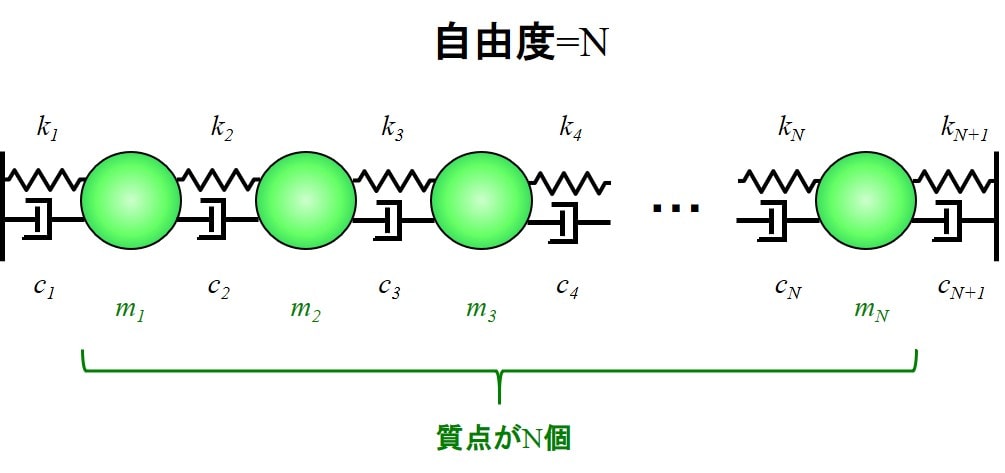
レイリー減衰は、多自由度系で減衰を取り扱うために使われます。
よって、上記のようなN自由度系のモデルで話を進めていきます。
なお、運動方程式は、\([M]\)を質量マトリックス、\([C]\)を減衰マトリックス、\([K]\)を剛性マトリックスとして、
$$[M]\ddot{X}+[C]\dot{X}+[K]X=0$$
と書けます。
モード解析法を使うために
さて、この運動方程式を解くために、モード解析法を用いて、計算量を減らすことを考えるわけです。
モード解析法は過去の記事で解説していますので、詳細はそちらを参考にして頂きたいのですが、
モード解析法の要点は、 \([M]\)や\([K]\)を対角化することで、N元連立微分方程式をN個の微分方程式に座標変換する方法、 でしたね。
で、前回までは減衰の\([C]\)というものが無かったわけですが、減衰もちゃんと考えるために、レイリー減衰というものを仮定します。
レイリー減衰は下記のように表されます。
$$[C]=α[M]+β[K]$$
なお、レイリー減衰を仮定したときの減衰比を\(ζ\)とすると、
$$ζ=\frac{α}{2ω}+\frac{βω}{2}$$
となります。
詳細は後述しますね。
このレイリー減衰は、 空気抵抗や摩擦、といった粘性減衰とは異なり、モード解析で使うために仮定した、いわゆる計算を楽にするための減衰です。
でもこのレイリー減衰を使うと、いろんな物理現象を表すこともできるので、よく使われる減衰となっています。
レイリー減衰を用いるとどうなるか?
それではレイリー減衰を運動方程式に代入してみましょう。
このままだと、ただ複雑になっただけのように見えますので、ここからモード解析法を使います。
つまり、この運動方程式を変換行列\([P]\)を用いて各項を対角化していきます。
変換行列は、 減衰が無い運動方程式が解を持つ条件から、固有値、固有ベクトルを求め、その固有ベクトルを列ベクトルとして並べた行列となります。
具体的にはi次の固有ベクトルを\(\vec{u}^{(i)}\)と下図のように書けます。
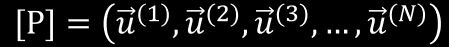
まず、この変換行列の逆行列\([P]^{-1}\)を左側からかけると、
つぎに\(X\)と各マトリックスの間に\([P][P]^{-1}\)を挿入して、
このように書き表すことができますね。
ここで、\([M]\)と\([K]\)については変換行列[P]で挟むことで対角化されており、対角化した行列をそれぞれ\([m]\)、\([k]\)とすると、
$$[P]^{-1}[M][P]=[m]$$
$$[P]^{-1}[K][P]=[k]$$
と書けます。
また、モード座標系を導入して、 \([P]^{-1}X=q\) としますと、運動方程式は、
減衰の項だけ取り出して、カッコを外してあげると、
となります。
この質量マトリックス\([M]\)の部分と剛性マトリックス\([K]\)の部分は、変換行列\([P]\)で挟み込まれて対角化されるので、
$$α[m]+β[k]$$
と書き直すことができます。
よって運動方程式は下記のようになります。
この運動方程式に含まれる行列は全て対角化されている行列なので、N個の微分方程式が並んだ状態になるわけですね。
つまり レイリー減衰を用いてモード解析法を使うと、減衰の部分も対角化出来て、連立微分方程式を解く必要がなくなります。
レイリー減衰の特徴
レイリー減衰を用いたときの減衰比ζは周波数依存性があり、周波数が低いとαに、周波数が高いとβに依存します。
はい、いきなりわけわからーん!となりそうなので、運動方程式からたどっていきましょう。
運動方程式は下記ですね。
行列で書くと下図のようになります。
このように書いたとき、1つ目の運動方程式を取り出すと、
となります。
減衰の項の部分を\(c_1^*\)と置くと下記のようになります。
$$m_1^*\ddot{q}+c_1^*\dot{q}+k_1^*q=0$$
運動方程式を解くときに、固有振動数\(ω\)と減衰比ζを使って書き表すと式がスッキリするので書き換えましょう。
$$ω_1=\sqrt{\frac{k_1^*}{m_1^*}}$$
$$ζ_1=\frac{c_1^*}{2\sqrt{m_1^*k_1^*}}$$
これらを使うと運動方程式は、
このようになって、1自由度の減衰振動を解く形とまったく同じになるわけです。
ここで\(ζ_1\)についてもう少し式変形してみると、
αの項とβの項で分けて\(ω_1\)を用いて書くと、
$$ζ_1=\frac{α}{2ω_1}+\frac{βω_1}{2}$$
このようになり、減衰比ζの\(ω_1\)依存性を書くと下図のようになります。
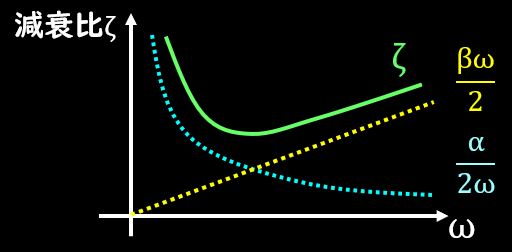
低周波数側でαの影響が大きく、高周波数側でβの項の影響が大きいことが分かりますね。
まとめ
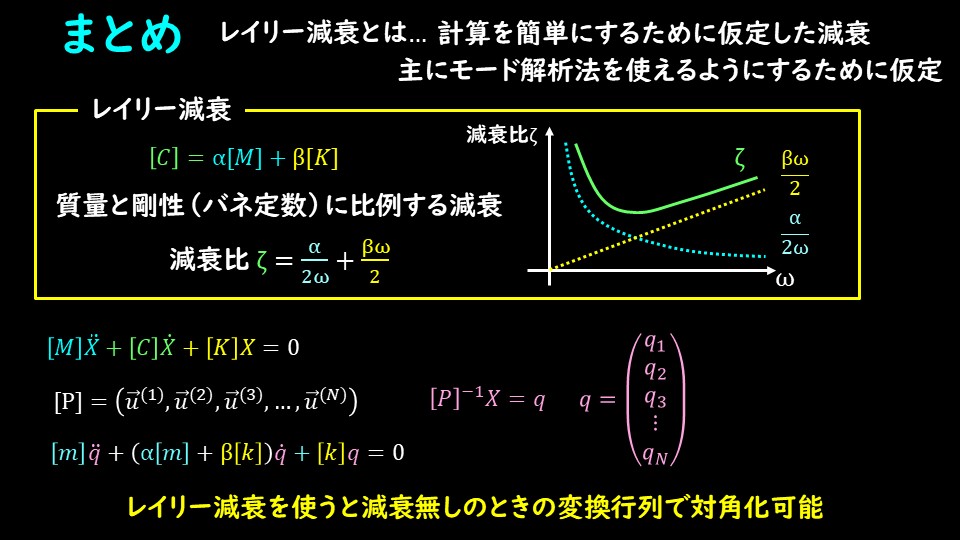
レイリー減衰について解説しました。
レイリー減衰はモード解析法で減衰振動を取り扱うために取り入れた減衰で、下記のように表せます。
$$[C]=α[M]+β[K]$$
このように減衰マトリックスを置くと、モード解析法で対角化することができ、計算が楽になります。
また減衰比ζは下記のような関係性があります。
$$ζ=\frac{α}{2ω}+\frac{βω}{2}$$
周波数が低いとαに、周波数が高いとβに依存します。
以上を理解して頂ければレイリー減衰の基本は抑えられていますので、わからない部分は本記事を読みなおしたり、動画を参考にして頂ければと思います。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎㉒-3 モード解析法での強制振動の取り扱い方をわかりやすく解説
