粘弾性と損失係数と減衰振動って関係あるの?


粘弾性と減衰は密接に関係しているから、今日は粘弾性と減衰振動の関係性を説明するね。
今日は粘弾性・損失係数と減衰振動について解説します。
物には粘性と弾性という性質があり、その両方を合わせて粘弾性と呼びます。
粘性が大きいと減衰が大きく、粘性が大きい物体を振動させると、減衰が大きな減衰振動になります。
これらの詳細について解説していきますね。
粘弾性以外の減衰についても過去の記事で解説していますので、そちらを参考にしていただければと思います。
また、動画でも解説していますので、是非こちらも参考にしていただければと思います。
粘弾性

粘弾性は『粘性』と『弾性』を合わせて粘弾性と呼びます。
粘弾性=粘性+弾性 というイメージですね。
そもそも粘性とか弾性とか何なの?という方のために、それぞれを簡単に説明しますね。
弾性

まず弾性です。
これはフックの法則に従う性質です。
フックの法則は材料力学等では下記のように書きます。
$$σ=Eε$$
\(σ\)は垂直応力、\(E\)は縦弾性係数(ヤング率)、\(ε\)はひずみを示します。
高校物理では下記のようにバネの式を習った方が多いのではないでしょうか?
$$F=kx$$
\(F\)はバネの力、\(k\)はバネ定数、\(x\)が変位です。
これらは両方とも、 [力]=[硬さを示す係数]×[変位量] という形になっています。
位置の変化に比例して力が発生する性質が弾性です。
バネのエネルギーを弾性エネルギーと言ったりしますね?その弾性です。
粘性
粘性についてですが、これはニュートンの法則に従う性質です。
$$σ=μ\dot{ε}$$
先ほどの弾性の時と同様に、\(σ\)は応力、\(ε\)はひずみでμは粘度を示します。
ニュートンの法則は高校物理では習わない内容(流体力学などで習う内容)なので、なじみのない方も多いかもしれません。
ニュートンの法則の右辺を見て頂きたいのですが、\(\dot{ε}\)とひずみの時間微分したものが存在します。
これはひずみが単位長さあたりの位置の変化量を示しているので、その時間微分は、速度ひずみを示すことになります。
粘性は速度勾配に比例して力が発生する性質、となります。
粘弾性の例

具体的にどういう物質が粘性が大きいの?
弾性は、力が変位に比例する(フックの法則)、粘性は、力が速度に比例する(ニュートンの法則)と理解して頂いたところで、
具体的にどういう物質が粘性が大きくなっていて、どういう物質が粘性が小さいのか、を示したいと思います。
こちらがそのイメージです。

硬い金属などは粘性が小さく、ゴムとかガムとかは粘性が大きい性質があります。
ワンピースのルフィとかはゴム人間なので、粘性が大きいということになりますね。
粘性と減衰について
それでは、この粘性と減衰の関係性についてです。
減衰振動でよく扱う減衰の種類として、粘性減衰というものがあり、この減衰と非常に関わりが強くなっています。
まぁ名前からしても『粘性減衰』っていうくらいなので、粘性と関係性がありそうなのは容易に想像つきますよね。
粘性減衰というのは、速度に比例した減衰力を発生させるものでした。
モデルを書くと、下記のようにダンパー(ダッシュポット)が質点についたような図になりますね。
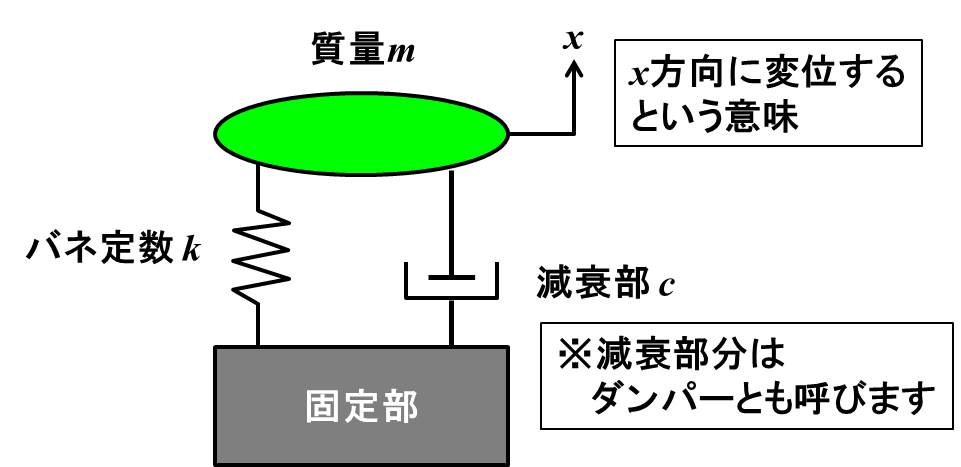
粘性減衰の大きさ\(F\)は、減衰係数を\(c\)とすると、
$$F=cv=c\dot{x}$$
となります。
この式を見て頂くと、ニュートンの法則とそっくりであることがわかりますね。
つまりは『減衰係数=粘度』とすると、粘性の物体に振動を与えたとき、粘性が減衰を表すことになります。
もっとざっくり言い換えると、 『粘性が大きいと減衰が大きくなる』 ということになります。
減衰が大きいということは力を吸収するという風にも言い換えることができるので、 ゴムゴムのルフィには打撃(力)が効かないわけですね。
粘性と減衰振動の波形の関係
金属のような粘性が小さい場合の自由振動波形は下図のような波形になります。
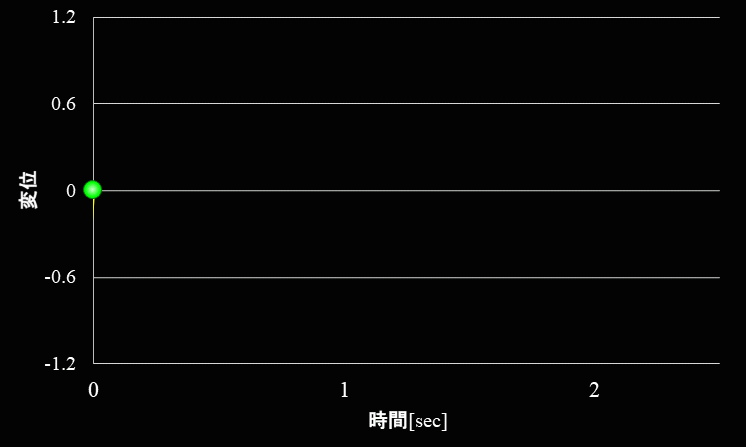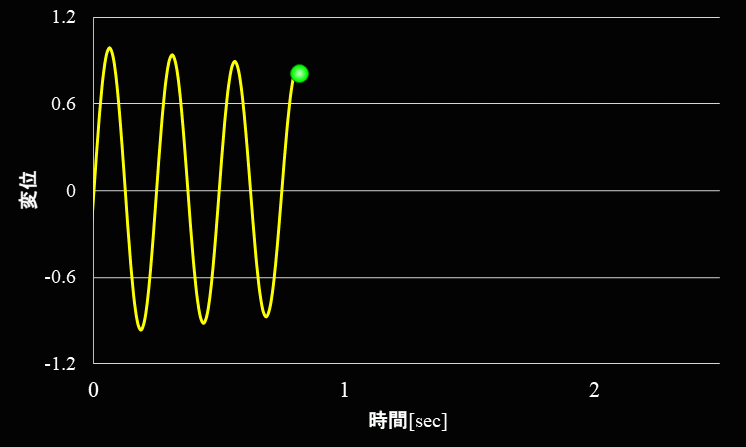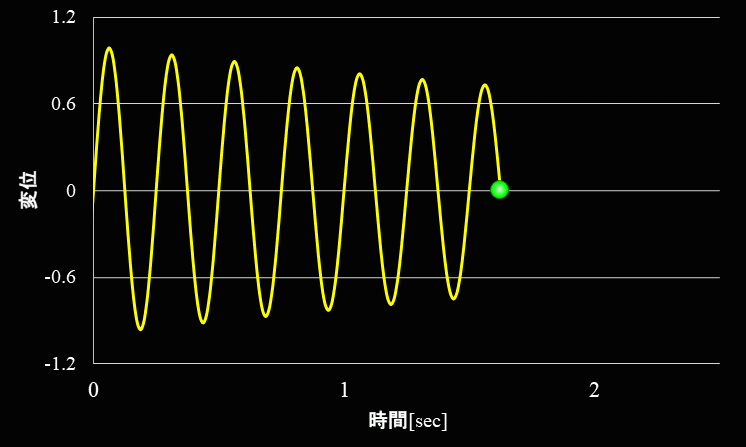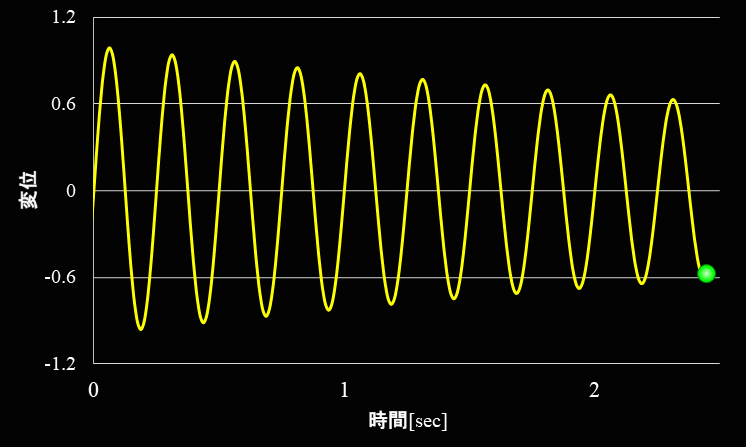
一方、ガムやゴムのような粘性が大きい場合の自由振動の波形は下図のようになります。
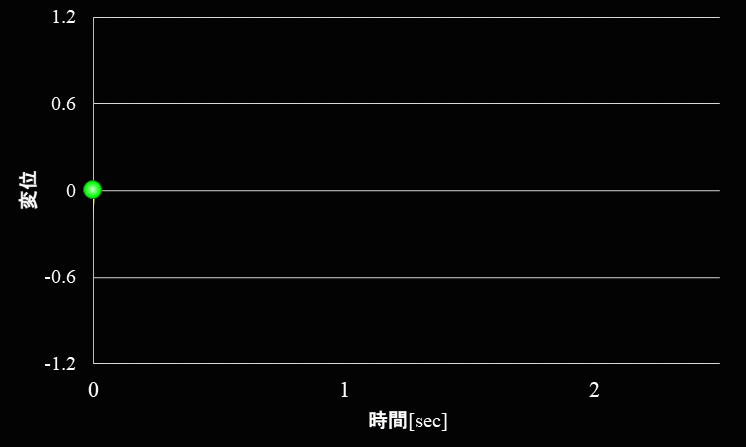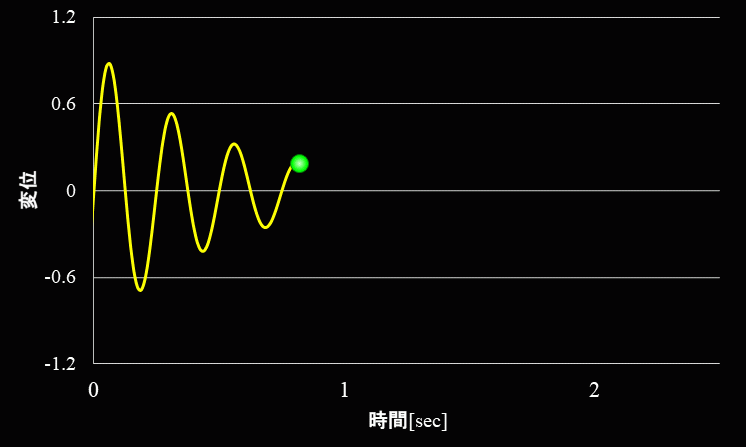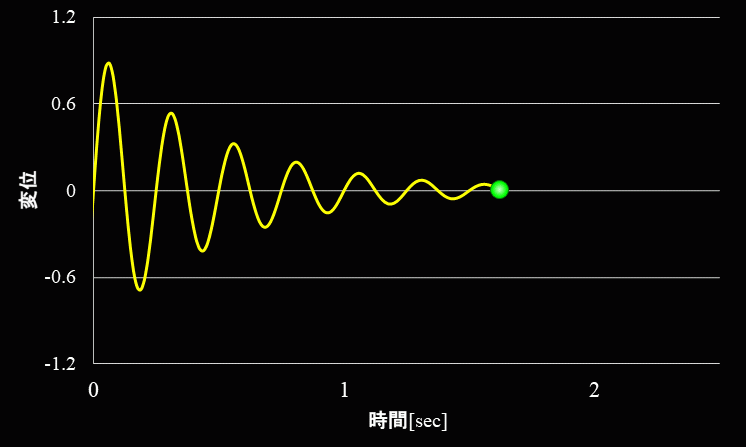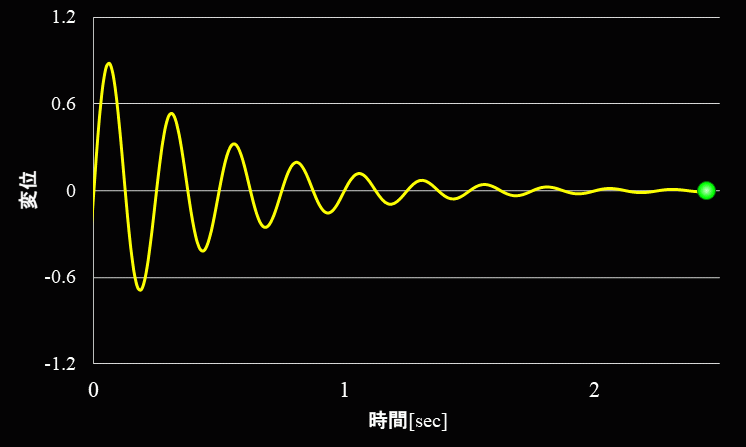
金属などの粘性の低い物質では、振幅の小さくなる度合いが緩やかに対して、ゴムやガムなどの粘性が高い物質を振動させると、 振幅は急激に減少していきます。
粘弾性と損失係数
次は損失係数について説明します。
損失係数は\(η\)(イータ)や\(tanδ\)で表され、 粘性と弾性の比、というイメージです。
(厳密には固有振動数\(ω\)が入ってきます)
\(η\)や\(tanδ\)は下記のようなつながりがあります。
$$η=tanδ=2ζ$$
損失係数\(η\)、\(tanδ\)が\(2ζ\)と一致するということを証明していきます。
弾性と粘性による力
先ほどあったように、弾性は変位に比例する力、粘性は速度に比例する力となります。
弾性の力を\(F'\)としてバネ定数\(k\)、変位を\(x\)とすると
$$F’=kx$$
粘性の力を\(F''\)として粘度\(μ\)とすると
$$F’’=μv=μ\dot{x}$$
ここで粘性減衰を仮定し、減衰係数\(c\)と粘度\(μ\)が等しいとしますと、
$$F’’=cv=c\dot{x}$$
このように表すことができます。
ところで、これら\(F'\)と\(F''\)は数学的には単純に足し合わせることができません。
例えば、\(x=cosωt\)とすると、\(\dot{x}=-ωsinωt\)となって、
$$F'+F’’=kcosωt-cωsinωt$$
となりますので、1つの項にまとめることはできないですよね?
(三角関数の合成を使えばまとめることはできるのですが、今回は単純な足し合わせということで、三角関数の合成は使わないということにしてください)
基本的に微分した項と微分していない項は分けて書くことが普通なのです。
なので、これらは1次独立的な状態にあることが多いわけです。
特に振動工学で取り扱うような変位が三角関数で表される状況だと、1次独立的な状態になります。
つまり、微分した項(粘性の項)と微分していない項(剛性の項)は、ベクトルで考えると、同じ方向を向いておらず、
独立したベクトル2本(粘性のベクトルと剛性のベクトル)を考える必要があるわけですね。
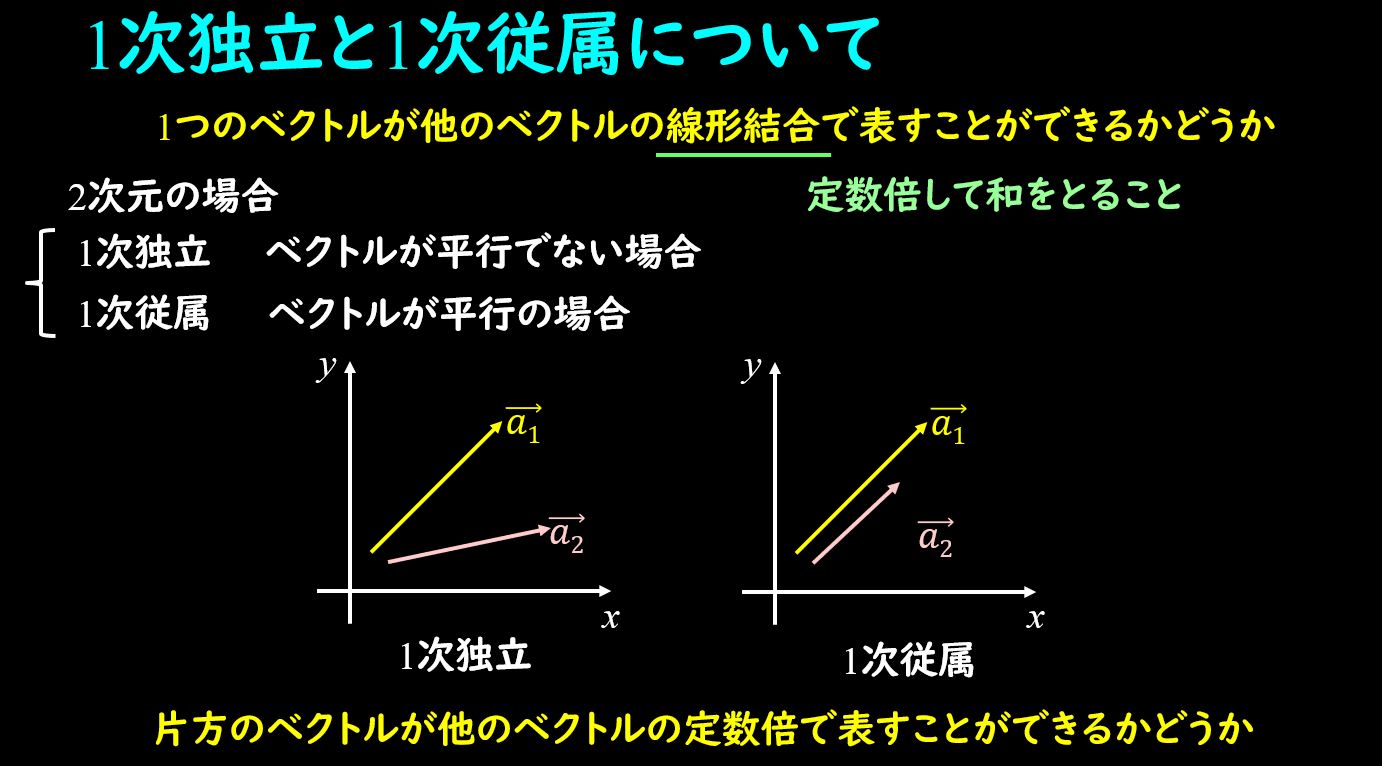
上図でいうところの\(\vec{a_1}\)と\(\vec{a_2}\)がそれぞれ粘性、剛性のベクトルとなっていて、1次独立の状態になっている、ということになります。
で、これをもっとスマートに図的にも式的にも表すためにどうすればよいか?と考えると、高校数学でも学んだ『複素数』を用いるとキレイに表せることに気づくわけです。

そんなもん気づくわけねーだろ!!
そんなツッコミが入りそうですが、振動工学などの物理系で
『複素数を使って、2つの軸のものを同時に考える』
という考え方は、よくやる手法なので、気づかなかった人は覚えておきましょう。
それではどのような力が発生するか、複素数を使って表していく、ということを理解していただいたところで、
物体が振動したときにどのような力が発生するかを見ていきます。
物体が変位\(X_0e^{iωt}\)で時間的に振動しているとすると、弾性の力は
$$F'=kx=kX_0e^{iωt}$$
粘性からの力は
$$F’’=c\dot{x}=iωX_0e^{iωt}$$
物体にはたらく力は弾性の力と粘性の力の和になるので、
$$F=F'+F’’=(k+icω)X_0e^{iωt}$$
このようになるのですが、この式の\(X_0e^{iωt}\)は、物体の変位そのものになっているので、
発生している力\(F\)は\(k+icω\)×変位というように、変位量に比例していると見ることができます。
この時の係数\(k+icω\)を複素弾性率\(G\)と呼び、
$$G=k+icω$$
と書くことができます。
複素弾性率\(G\)の実部と虚部をそれぞれ\(G'\)、\(G’’\)とすると下記のようになります。
$$G=G'+iG’’=k+icω$$
損失係数\(η\)は粘性と弾性の比となりますので、
$$η=tanδ=\frac{G''}{G'}$$
と表すことができ、下記のようになります。
$$\frac{G’’}{G'}=\frac{cω}{k}$$
これは複素数平面上に図で書くと下図のようになります。
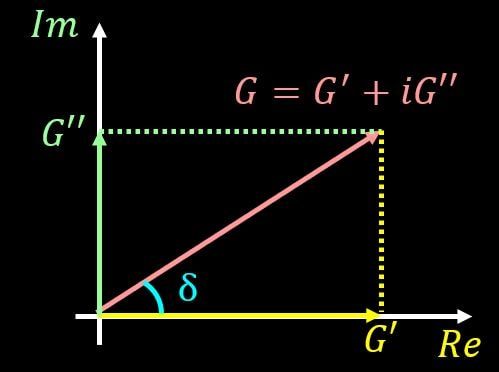
\(G\)と実軸がなす角が\(δ\)となって、傾きが\(tanδ\)となっています。
この傾きは粘性と弾性の比\(\frac{G’’}{G'}\)そのものを示していますね。
損失係数を計算する
ここで、減衰比\(ζ\)は下記のように表すことができますので、\(c\)を\(ζ\)に置き換えましょう。
$$ζ=\frac{c}{2\sqrt{mk}}$$
$$\frac{cω}{k}=\frac{2ζω\sqrt{mk}}{k}=2ζω\sqrt{\frac{m}{k}}$$
\(ω\)の部分については
$$ω=\sqrt{\frac{k}{m}}$$
となるので、代入すると、
$$2ζω\sqrt{\frac{m}{k}}=2ζ$$
このようになり、損失係数\(η\)が\(2ζ\)と等しくなります。
複素弾性率について
さて、複素弾性率\(G\)が急に出てきたのですが、ここで、もう少し詳しく説明します。
複素弾性率は、下記のように実部と虚部をわけて表すことができるのでしたね。
$$G=G'+iG’’$$
この\(G'\)を貯蔵弾性率、\(G’’\)を損失弾性率と呼びます。
貯蔵・損失の意味

\(G'\)や\(G''\)の貯蔵や損失というのはどういう意味があるかについてですが、これはエネルギーの観点の話となります。
損失弾性率G’’
損失係数\(tanδ\)は粘性と弾性を示していて、\(tanδ\)が大きい=粘性が大きく減衰が大きいということになります。
さて、減衰が大きいとエネルギーがどのようになるか、について考えていきたいのですが、詳細は下記の過去記事で解説していますので参考にしていただければと思います。
ここでは簡単に説明しておきますと、振動に減衰が含まれると、エネルギーがロスされていくのでした。
そのエネルギーロス量を示すものが、散逸関数\(D\)と呼ばれるもので、
$$D=\frac{1}{2}cv^2$$
と、減衰係数と速度で表すことができ、減衰係数が大きいとエネルギーロスが大きくなることを示しています。
粘性減衰を仮定している場合、減衰係数cが大きい、ということは粘性が大きいと言い換えることができますので、
粘性が大きい=エネルギーロスが大きい
ということになります。
すなわち、エネルギーを損失する、ということになるわけですね。
\(G’’\)は複素弾性率の虚部の部分で、粘性の部分に相当するパラメータなので、損失弾性率、という名前がついているわけです。
貯蔵弾性率G'
一方、貯蔵弾性率は複素弾性率の実部を示していますので、バネ定数\(k\)と同義になります。
この部分のエネルギーについては、バネの弾性エネルギー\(K\)で表すことができて、
$$K=\frac{1}{2}kx^2$$
となりますね。
これも過去の記事で解説していますので、詳細はそちらを参考にしていただければと思います。
この弾性エネルギーは、振動している間は、運動エネルギーに入れ替わったりするエネルギーとなり、系の外にエネルギーが出ていくわけではありません。
つまり、系全体でエネルギー保存が成り立つエネルギーとなりますので、その意味をこめて『貯蔵』弾性率と呼んでいるわけです。
エネルギーが系全体に貯蔵されるか、系外に出て行って損失するか、ということを貯蔵弾性率と損失弾性率が表しているんですね。
そして、その損失弾性率と貯蔵弾性率の比が、粘性と弾性の比を表していて、損失係数\(η\)、\(tanδ\)とつながっている、ということになっています。
まとめ
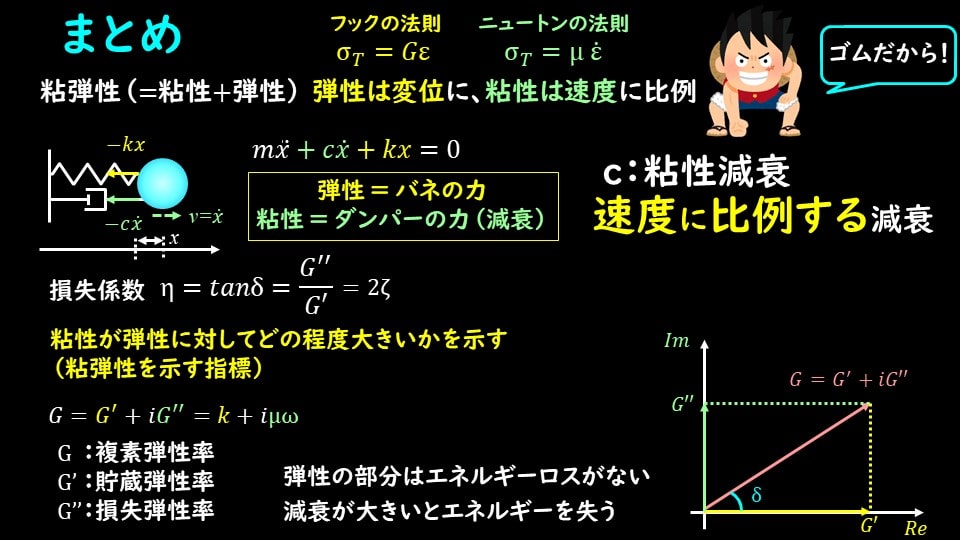
本日は、粘性減衰を仮定した場合、粘弾性と損失係数、減衰振動との関係性を解説しました。
『粘性』と『弾性』を合わせて粘弾性と呼び、粘弾性=粘性+弾性と表すことができます。
粘性は速度ひずみに比例して発生する力(ニュートンの法則)、弾性は変位に比例して発生する力(フックの法則)です。
減衰振動を考えるにあたって、粘性減衰を仮定すると、振動の減衰部分が、粘性を表して、バネの力が弾性を表すことになります。
損失係数\(η\)、\(tanδ\)は、粘性と弾性の比に表していて、粘性が弾性に対してどの程度大きいかを表しています。
この損失係数\(η\)、\(tanδ\)は、エネルギー的な観点で見ると、損失弾性率、貯蔵弾性率の比で表すことができて、
損失弾性率は粘性の部分を、貯蔵弾性率は弾性の部分を表しています。
この損失・貯蔵というのは、振動したときにエネルギーが系から損失していくのか、貯蔵されるのか、を示していました。
これら損失弾性率、貯蔵弾性率を複素数を用いて複素数平面上に図示したとき、複素弾性率と実軸のなす角が\(δ\)となり、傾きが損失係数\(tanδ\)となります。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎 振動をエネルギーの観点から理解する-減衰振動、散逸関数
