この記事は下記の減衰振動で出てきた2階の線形微分方程式を解いた結果を、もう少し詳しく解説します。
参考記事
まずは復習で2階の線形微分方程式について、説明し、双曲線関数の説明をします。
2階の線形微分方程式
下記のような式を2階の線形微分方程式を考えます。
$$ζ = \frac{c}{2\sqrt{mk}}$$
$$ω = \sqrt{\frac{k}{m}}$$
これは減衰を考慮した振動の運動方程式ですね。
ζは減衰比、ωは固有振動数を示します。
解の求め方(簡易版)
詳細は参考記事を見てくださいね。
参考記事
これを解くためには、微分しても関数系が変わらない解を仮定してから、一般解を求めます。
$$x = Ae^{λt} Aは定数$$
このように指数関数の解を仮定して、運動方程式に代入すると、
となるので、λの部分の2次方程式がゼロになると、すべての$t$で成立しますね。
この2次方程式を特性方程式と言い、この解は
となります。
このルートの中の\(ζ^2-1\)が1以上のとき、どのようになるか、について解説します。
双曲線関数
双曲線関数というものを使用しますので、この関数について説明します。
関数の形
双曲線関数
- \(sinhx = \frac{e^x-e^{-x}}{2}\)
- \(coshx = \frac{e^x+e^{-x}}{2}\)
- \(tanhx = \frac{e^x-e^{-x}}{e^x+e{-x}}\)
グラフ
\(sinhx、coshx、tanhx\)のグラフを下記に示します。
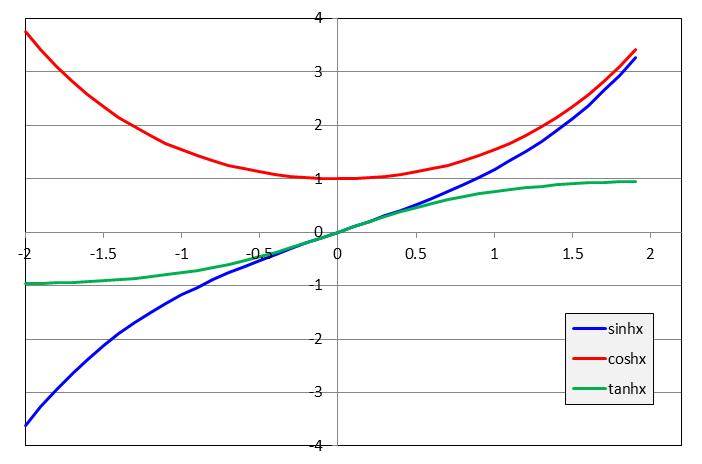
この関数の形って振動と関係あるの??


振動している領域では使わないんだけど、減衰を大きくした過減衰の状態で少し使うんだよ
一般解の求め方
線形微分方程式の一般解は、任意定数を含む2つの解の足し合わせ、となります。
\(x_1 = e^{λ_1 t}、x_2 = e^{λ_2 t}\)としますと、下記のようになりますね。
特性方程式の解は下記の通りで、\(ζ>1\)のときを考えます。
二つの解を\(λ_1、λ_2\)とすると
となり、これを一般解の式に代入して、整理します。
これが過減衰の式ということなのですが、本記事ではこれを双曲線関数で示します。
双曲線関数での表記の導出
まず、\(ω\sqrt{ζ^2-1} = γ\)と置いて変形すると
この式を双曲線関数で示そうと思います。
適当な定数\(A、B\)を用意し、\(Acoshx\)と\(Bsinhx\)の和の式を変形していきます。
これらを\(e^x\)と\(e^{-x}\)で整理しますと、
となります。
運動方程式の一般解の式に似てきましたね。
\(C_1= \frac{A+B}{2}、C_2=\frac{A-B}{2}、x = γt\)とすると
この式から一般解は双曲線関数を使って表すと下記のようになります。
さて、この式がどのような関数になるか、についてが重要ですね。
eの指数部分ωζと双曲線関数のγのどちらが大きいかで、関数の形は変わります。
(双曲線関数もeの指数関数なので、どちらが強いかは指数関数の指数部分の大きさ次第ということです)
しかし、\(ω\sqrt{ζ^2-1} = γ\)と置いていますので、
\(ωζ > γ =ω\sqrt{ζ^2-1}\) ですね。
この場合のグラフを下記に示します。
なお、\(fx = e^{2x}(coshx+sinhx)\)として黒線で示しています。
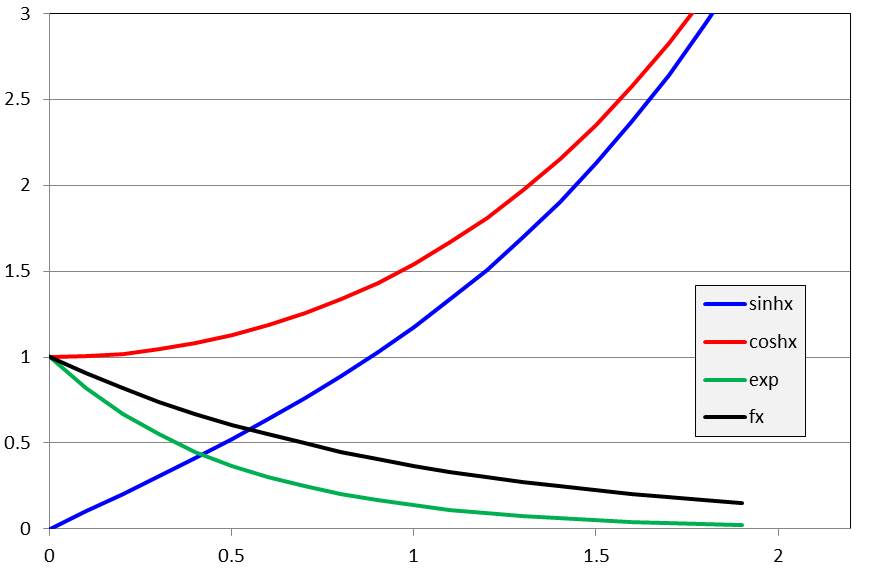
黒線は単調減少のグラフになっていることがわかりますね。
ちなみに緑の線はζ=1で双曲線関数がゼロになったとき、すなわち臨界減衰の形と一致します。
最後にζで場合分けした減衰の振動のグラフを示して終わります。

まとめ
過減衰の部分の計算について詳細を説明しました。
双曲線関数を\(exp\)を用いて指数関数で表記すれば、一般解からグラフの形は想像しやすくなりますね。
どのような関数か、イメージをもっていただければ理解しやすくなりますので、関数の形は覚えておきましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
