[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]単振動の式ってなんで三角関数になるの？[/voice]
[voice icon="https://deltapower.site/wp-content/uploads/2020/09/にっこり右側.jpg" name="デルタ先生" type="r"]これは運動方程式を解くことで、三角関数が出てくるからなんだ。今日は実際に運動方程式を解いてみよう。[/voice]
高校物理で単振動の式を習ったとき、
『振動は三角関数で表すことができる』
と習いませんでしたか？（私もこう習いました）
しかし、なぜ三角関数で表すことができるかまで説明してくれる先生は少ないですよね？
今回は運動方程式を解くことで、三角関数を導出します。
微分方程式を解く必要がありますが、初めてでも理解できるように解説しますので、最後まで理解できるように頑張りましょう！
[box class="blue_box" title="参考記事"]
[/box]
[box class="green_box" title="本記事をおススメする人"]
- 単振動の運動方程式を解きたい人
- 振動の式が三角関数になることに疑問を持った人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
[/box]
単振動の復習と求める変位の式
まずは単振動とはどんな運動か、復習しておきましょう。
下記のような、ずーっと同じ振幅、同じ周波数で振動するような振動のことを『単振動』と言います。
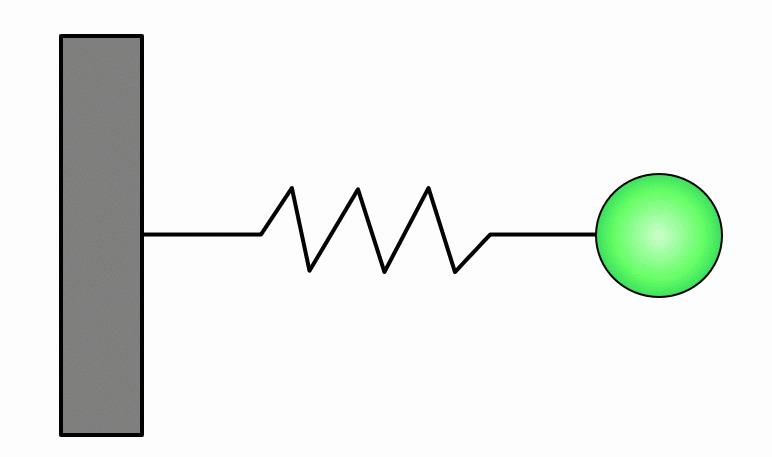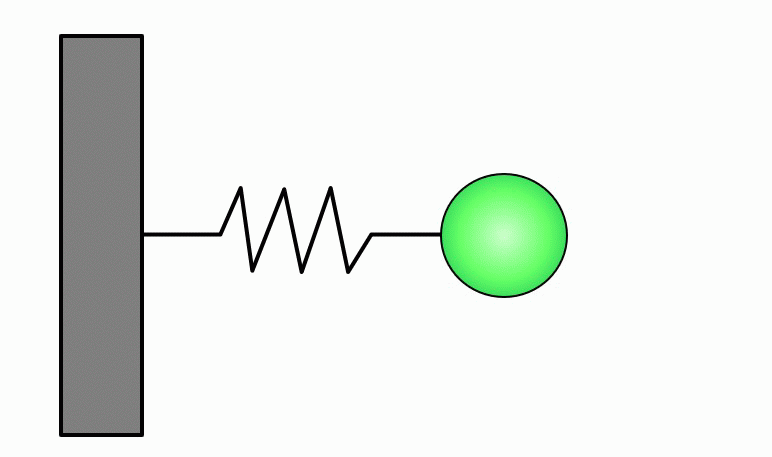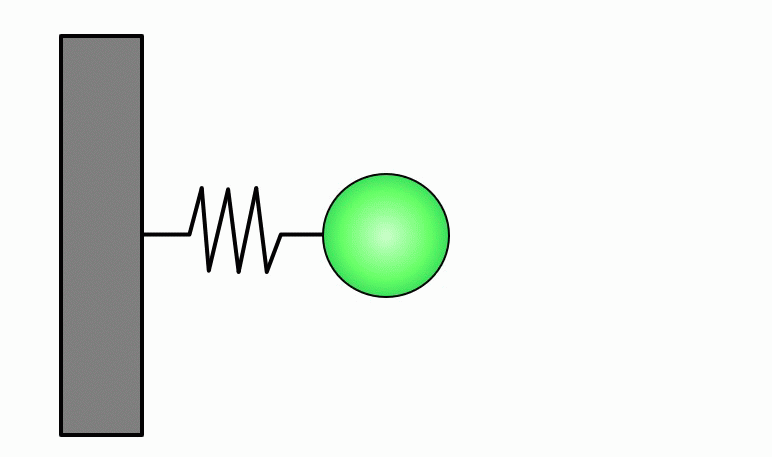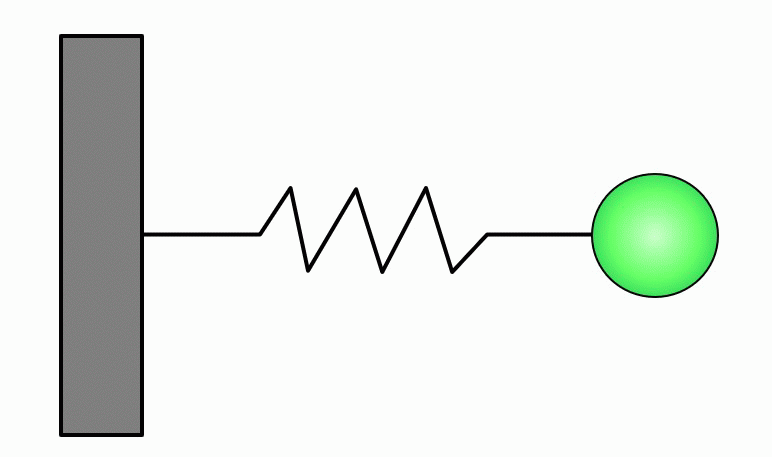
バネが自然長の長さのとき、質点の位置を原点として、そこからバネが伸び縮みした量を変位と呼んで$x$とします。
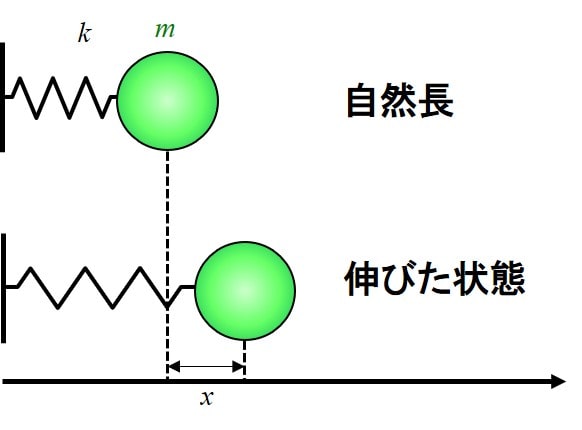
この時、$x$の式は
$$x(t)=Asin(ωt+φ)\tag{1}$$
と表される、と高校物理で習いましたね？
今回、これを運動方程式を解くことで、なぜ三角関数が出てくるかを示します。
単振動の運動方程式
図のように、バネにつながれた質点を考え、質点の質量をm、バネ定数をkとします。
バネが自然長の長さのときのx座標を0として、右方向を正の方向と定義すると、バネの力Fは
$$F=-kx$$
となりますね。
これはフックの法則から求まります。
フックの法則を忘れてしまった人はこちらの過去記事を参考にしてください。
運動方程式は$ma=F$で、$a$は加速度なので、変位量$x$を時間で２回微分した$\ddot{x}$と等しく、
$$m\ddot{x}=-kx\tag{2}$$
これが単振動の運動方程式ですね。
単振動の運動方程式を解く
さて、(2)式の単振動の運動方程式を解いて、(1)の式のように、変位の式が三角関数になることを示していきます。
(2)式の運動方程式は、xの時間微分が入っている方程式なので、微分方程式となっています。
この微分方程式の解き方を解説していきますね。
単振動の運動方程式の解き方
$$m\ddot{x}=-kx\tag{2}$$
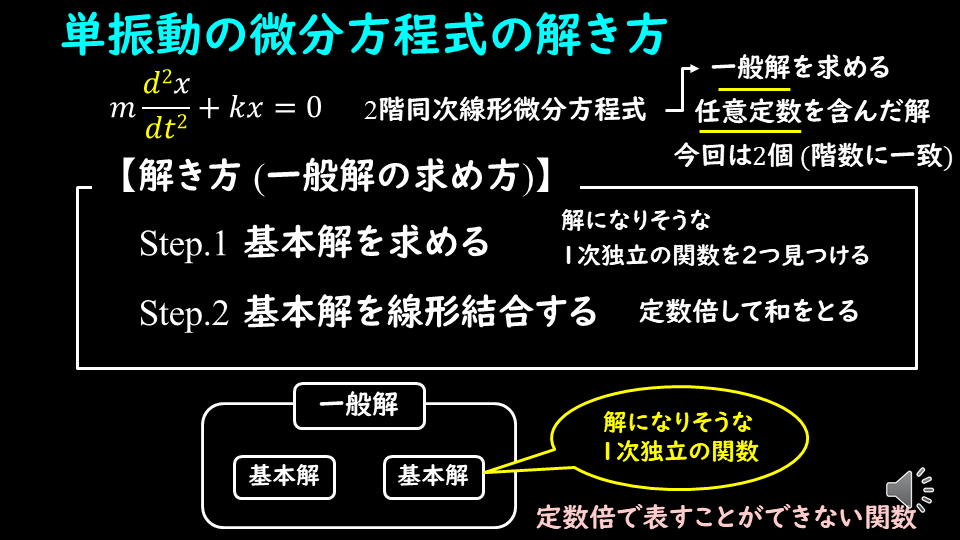
この(2)式は2階の同次線形微分方程式と呼ばれるもので、解き方がある程度決まっています。
[box class="pink_box" title="解き方の方針"]
- 微分方程式を満たしそうな解（基本解）を見つける
- 基本解を線形結合して、一般解を求める
[/box]
微分方程式で求めるものは、x=2とかx=1とかの数値ではなく、 関数を求めます。
解である関数を『一般解』と呼んでおり、この一般解を求めることが微分方程式を解くことになります。
一般解の中でも特殊なケースとして『基本解』と呼ばれるものがあり、その基本解の線形結合をすることで、一般解となる、ということも覚えておきましょう。
2階の微分方程式の場合、基本解は2つで、基本解の性質として、2つの基本解は1次独立である必要があります。
簡単には 1次独立とはお互いが定数倍で表すことができない、と考えていただければと思います。
このあたりの詳細の数学はこちらの過去記事を参考にしてください。
基本解を求める
(2)式を少し変形します。
$$\ddot{x}=\frac{k}{m}x\tag{3}$$
(3)式を解くにあたって、式の意味を考えてみましょう。
『xを2回時間微分すると、もとのxに－がついて定数倍されて戻ってくる』、
ということを示しています。(xは数ではなく、tの関数であることに注意！）
そんな関数に心当たりはありませんか？？
・・・答えは『$sin$』や『$cos$』ですね。
これら三角関数は2回微分されると、符号が逆転して元の三角関数に戻ります。
また、$sin(At)$のように、tの前に係数があると、2回微分すると$-A^2sin(At)$となり、
三角関数が定数倍されますね。
今回、この定数をωとすると、
$$ω=\sqrt{\frac{k}{m}}$$
と書くことができます。
よって、解の一つとして、
$$x=sin(ωt)\tag{4}$$
が得られます。
心配な方は(2)式の運動方程式に代入してみましょう。
基本解の線形結合
[voice icon="https://deltapower.site/wp-content/uploads/2020/04/男性悩み.png" name="物理苦手君" type="l"]あれ？さっきcosも解になるって言わなかった？[/voice]
[voice icon="https://deltapower.site/wp-content/uploads/2020/09/にっこり右側.jpg" name="デルタ先生" type="r"]そうだよ。cosも解の一つになるね。[/voice]
ということで、cosの方の解を書いておきましょう。
$$x=cos(ωt)\tag{5}$$
これも(2)の運動法手式に代入すると成立しますね。
ここまで来たら次のステップ、基本解の線形結合をとる、に移ります。
下記を線形微分方程式の性質として覚えておきましょう。
『一般解は基本解の線形結合、つまり定数倍して足し合わせた形になる』
今回、(4)や(5)で求めたsin、cosの解は1次独立の関係にあり基本解です。
sinは定数倍してもcosにならないですし、cosも定数倍してもsinになりませんので、1次独立です。
一般解を求めるためにこれらを和の形で表しましょう。
AとBを任意定数として、
(4)と(5)の線形結合より、
$$x=Asin(ωt)+Bcos(ωt)$$
三角関数を合成して一つにまとめると
$$x=\sqrt{A^2+B^2}sin(ωt+φ)$$
$$sinφ=\frac{B}{\sqrt{A^2+B^2}}$$
$$cosφ=\frac{A}{\sqrt{A^2+B^2}}$$
$\sqrt{A^2+B^2}$が見づらいのでこれを定数Cと改めておくと、
$$x=Csin(ωt+φ)\tag{6}$$
この(6)式が一般解の形です。
最初に説明した高校で習った単振動の変位の式である(1)と同じ形ですね。
このように、 運動方程式を解くと、三角関数の形で解が求まるので、三角関数で振動を表現できるわけです。
まとめ
今回は単振動の運動方程式を解くことで、変位の式を導き出し、三角関数で表現できることを解説しました。
解くに当たって微分方程式を解く必要があるので、微分アレルギーの人は苦労するかもしれませんが、微分方程式は解き方がある程度決まっています。
今回の単振動のケースは非常に簡単なパターンですので、ぜひマスターしておいてください。
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
参考文献
- 振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店