ラプラス変換表があるのはわかったんだけど、実際の微分方程式にどうやって使えばいいの?


ラプラス変換表の形にするために、少し式変形をしないといけないケースは多いんだ。ちゃんと使えるように式変形のルールをしっかり把握しておこう。
ラプラス変換表を使ってラプラス変換をしようとしたけど、どうやって使うかわからない人!
本記事では具体的にラプラス変換表を使ってラプラス変換をしていきます。
最後まで読んでいただければ、ラプラス変換表の使い方を理解できますので、頑張って理解していきましょう。
本記事をおススメする人
- ラプラス変換表について理解したけど、使い方がよくわからない人
- ラプラス変換表を使うために、ラプラス変換のルールを把握しておきたい人
ラプラス変換のおさらい
おさらいです。ラプラス変換のイメージを下記に示します。
\(t\)の関数から\(s\)の関数へ変換するのがラプラス変換で、ラプラス変換の公式は下記のようになるのでした。
$$F(s)=\int_0^\infty e^{-st}f(t)dt\tag{1}$$
この変換を使うと、微分方程式を解きやすくなるんですよ~、というのがラプラス変換。
でもラプラス変換を行う度に、積分するのも面倒なので、ラプラス変換表というものがありました。
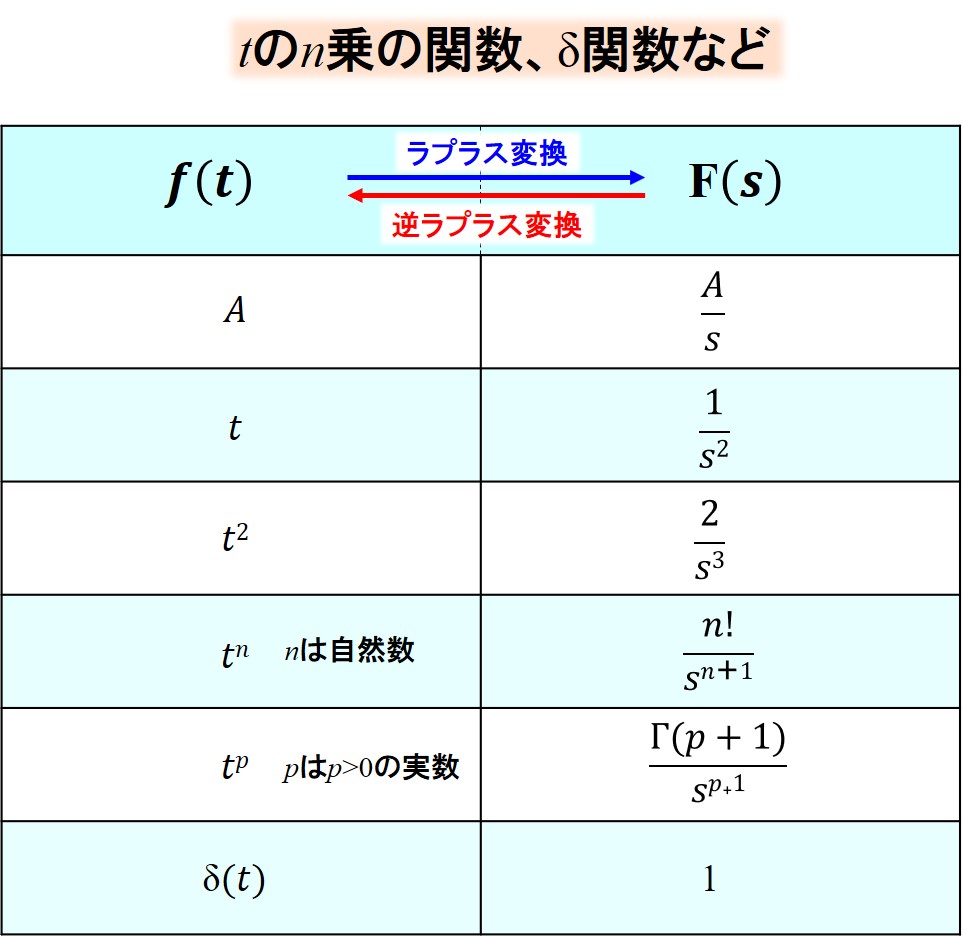
このラプラス変換表をそのまま使えることはレアケースなので、ラプラス変換表を使える形に変形できるようにルールを覚えておく必要があります。
ラプラス変換のルール
下記がラプラス変換のルールをまとめたものです。

特に重要なのが、微分・積分のルールで、このようになることはしっかり覚えておきましょう。
なぜならばラプラス変換は微分方程式に対して使いますので、この微分のルールを知らないとラプラス変換表を使うどころではありません。
実際にラプラス変換してみる
それではラプラス変換をしてみましょう。
\(f(t)\)、\(g(t)\)をラプラス変換したものをそれぞれ\(F(s)、G(s)\)とします。
ラプラス変換の記号を筆記体のLを用いて、
$$\begin{eqnarray}\mathcal{L}\left[f(t)\right]&=&F(s)\\\\\mathcal{L}\left[g(t)\right]&=&G(s)\end{eqnarray}$$
このように表すことにします。ただの表記の問題です。
簡単な例からやっていきましょう。
\(f(t)+g(t)\)のラプラス変換
例として、\(f(t)=t^2\)、\(g(t)=t\)として、
積分の中の\(t^2+t\)は分割できますので、
このように分解できます。
\(f(t)=t^2\)や\(g(t)=t\)という関数のラプラス変換は変換表からすぐに求めることができて、
$$F(s)+G(s)=\frac{2}{s^3}+\frac{1}{s^2}$$
となります。
\(af(t)\)のラプラス変換
\(a\)は定数ですので、\(a=2\)とし、\(f(t)=t^2\)とします。
$$\mathcal{L}\left[af(t)\right]=\int_0^\infty e^{-st}(2f(t))dt$$
\(t^2\)の係数の2は積分の外に出せるので、
$$2\int_0^\infty e^{-st}f(t)dt=2F(s)$$
\(f(t)=t^2\)なので、このラプラス変換は表からすぐ求まり、
$$2F(s)=\frac{2×2}{s^3}=\frac{4}{s^3}$$
このように求まります。
\(f(at)\)のラプラス変換
これは先ほどの$af(t)$のラプラス変換と間違いやすいので、\(a=2\)、\(f(t)=t^2\)として、計算してみます。
まず、\(f(t)\)のラプラス変換は変換表から、
$$F(s)=\frac{2}{s^3}$$
\(f(at)\)のとき、ラプラス変換の性質に当てはめると、
$$\begin{eqnarray}\mathcal{L}\left[f(at)\right]&=&\frac{1}{2}F\left(\frac{s}{a}\right)\\&=&\frac{1}{2}\frac{2}{(\frac{s}{a})^3}\\&=&\frac{a^3}{s^3}\\&=&\frac{2^3}{s^3}\\&=&\frac{8}{s^3}\end{eqnarray}$$
\(af(t)\)のラプラス変換の答えと異なることに注意してください。
\(e^{-at}f(t)\)のラプラス変換
\(a\)は定数ですので、\(a=2\)とし、\(f(t)=t^2\)とします。
$$\begin{eqnarray}\mathcal{L}\left[e^{-at}f(t)\right]&=&F(s+a)\\&=&\frac{2}{(s+a)^3}\\&=&\frac{2}{(s+2)^3}\end{eqnarray}$$
\(f(t-a)\)のラプラス変換
\(a\)は定数ですので、\(a=2\)とし、\(f(t)=t^2\)とします。
$$\begin{eqnarray}\mathcal{L}\left[e^{-at}f(t)\right]&=&e^{-as}F(s)\\&=&e^{-2s}\frac{2}{(s)^3}\end{eqnarray}$$
\(\frac{df(t)}{dt}\)のラプラス変換
この微分のルールは非常に重要ですので、使えるようにしておきましょう。
$$\begin{eqnarray}\mathcal{L}\left[\frac{df(t)}{dt}\right]&=&\int_0^\infty \frac{df(t)}{dt}e^{-st}dt\\&=&\left[f(t)e^{-st}\right]_0^\infty -\int_0^infty f(t)(-se^{-st})dt\\&=&-f(0)+s\int_0^\infty f(t)e^(-st)dt\end{eqnarray}$$
ここで\(F(s)=\mathcal{L}\left[ft)\right]\)とすると、上式は、
$$\begin{eqnarray}&=&-f(0)+SF(s)\\&=&sF(s)-f(0)\end{eqnarray}$$
ここで、例えば、\(f(t)=sinωt\)とすると、
$$\frac{df(t)}{dt}=ωcosωt$$なので、
$$\begin{eqnarray}\mathcal{L}\left[\frac{df(t)}{dt}\right]&=&\mathcal{L}\left[ωcosωt\right]\\&=&sF(s)-f(0)\end{eqnarray}$$
$F(s)$は$f(t)=sinωt$をラプラス変換したものであるから、ラプラス変換表より、
$$F(s)=\frac{ω}{s^2+ω^2}$$
また、\(f(0)=sin0=0\)なので、
$$\begin{eqnarray}\mathcal{L}\left[ωcosωt\right]&=&\frac{sω}{s^2+ω^2}\end{eqnarray}$$
\(cosωt\)のラプラス変換に\(ω\)をかけた式と同じになっていますね。
\(\int_0^t f(τ)dτ\)のラプラス変換
積分のルールも微分のルールと同じくらい重要ですので、使えるようにしておきましょう。
証明は省略します。
\(f(t)=t^2\)とすると、
$$\int_0^t f(τ)dτ=\frac{t^3}{3}$$
求めるべきは、このラプラス変換なので、
$$\mathcal{L}\left[\int_0^tf(τ)dτ\right]=\frac{F(s)}{s}$$
$F(s)$は$t^2$のラプラス変換なので、
$$F(s)=\mathcal{L}=\frac{2}{s^3}$$
となり、
$$\mathcal{L}\left[\int_0^tf(τ)dτ\right]=\frac{2}{s^4}$$
と求まります。
検算として、\(\frac{t^3}{3}\)のラプラス変換も同じ答えになることを確認しておきますと、
答えは一致しますね。
まとめ
ラプラス変換についてのルールを解説しました。
非常に重要な微分系と積分系は是非覚えておきましょう。
