本日は同次形の微分方程式の解法について解説します。
微分方程式って何??という方は下記の過去記事を参考にしていただいて、微分方程式のイメージをつかんでください。
同次形の微分方程式は、解き方と、『同次形だ!』と気付けるかがポイントになります。
本記事をおススメする人
- 微分方程式の変数分離は解けるけど、同次形の解き方を勉強をしたい人
- 微分方程式についてなんとなくわかったけど、解き方が分からない人
同次形の微分方程式
下記が同次形の微分方程式です。
$$y'=f(\frac{y}{x})・・・①$$
同次形の解法
解法5ステップ
- \(\frac{y}{x}=z\)と置きます。
- \(y=zx\)、\(y'=z'x+z\)とします(式変形と微分するだけ)
- 元の式を\(z'x+z=f(z)\)と置き換える。
- \(z'=\frac{dz}{dx}=\frac{1}{x}(f(z)-z)\)と式変形する。
- \(f_1(x)=/frac{1}{x}、g(z)=f(z)-z\)として、変数分離形で解く
\(\frac{y}{x}=z\)と置く→式変形→変数分離形の形にもっていく、という流れです。
\(z=\frac{y}{x}\)とおきます。
両辺に\(x\)をかけると
$$y=zx$$
これを\(x\)について微分します。\(z\)も\(x\)の関数であることに注意しましょう。
$$y'=z'x+z$$
①に\(y\)と\(y'\)を代入します。
$$z'x+z = f(z)$$
$$\frac{dz}{dx}=\frac{1}{x}(f(z)-z)$$
ここで、\(f_1(x) = \frac{1}{x}、g(z) = f(z)-z\)とすると、
$$\frac{dz}{dx}=f_1(x)g(z)$$
これは変数分離形の微分方程式ですね。
変数分離形の微分方程式の解き方の詳細については、下記の記事を参考にしてください。
さて、変数分離形の微分方程式の解き方は下記の5ステップですね。
解法5ステップ
- 両辺を\(g(z)\)で割る (\(g(z)≠0\)とする)
- 両辺に\(dx\)をかける
- 両辺に積分記号をつける
- \(z=○○\)の形に式変形
- \(g(z)≠0\)となるyの条件を満たすような積分定数Cを求める
両辺をg(z)で割って、両辺にdxをかけます。
$$\frac{dz}{g(z)} = f_1(x)dx$$
これを両辺積分して、実際に積分計算すれば解けるわけですね。
$$\int\frac{dz}{g(z)} = \int f_1(x)dx$$
あとのステップは具体的な関数が無いと進めませんので、次からの具体例で見ていきましょう。
具体例
それでは具体例で実際に同次形の方程式を解いていきましょう。
\(y'=\frac{y^2}{x^2+xy}\)
ん??これって同次形の微分方程式なの??


そうだよ、分母と分子を\(x^2\)で割ったらいいんだ。
まずは\(x^2\)で分母と分子を割ることに気付けるか、というところがポイントです。
$$y' = \frac{\frac{y^2}{x^2}}{1+\frac{y}{x}}$$
このように書くと、同次形になっていますね。
\(z=\frac{y}{x}\)とおくと、\(y=zx\)となり、
微分したy'は\(y'=z'x+z\)です。
もとの式は、
$$z'x+z = \frac{z^2}{1+z}$$
少し整理しましょう。
$$\frac{dz}{dx}x=\frac{z^2}{1+z}-z= \frac{z^2-z(1+z)}{1+z}$$
よって右辺は、
$$= \frac{-z}{1+z}$$
となります。
両辺を\(x\)で割ります。
$$\frac{dz}{dx}=\frac{1}{x} \frac{-z}{1+z}$$
ここまできたらあとは変数分離形で解くだけですね。
両辺を\(\frac{-z}{1+z}\)で割って、\(dx\)をかけましょう。
$$\frac{1+z}{z}dz=\frac{1}{x}dx $$
ここで\(z≠0\)としています。
次は両辺に積分記号をつけます。
$$-\int\frac{1+z}{z}dz=\int\frac{1}{x}dx $$
左辺の積分は
$$-\int(\frac{1}{z}+1)dz = -log|z|-z+C$$
\(C\)は積分定数です。
右辺も計算すると、
$$-log|z|-u+C=log|x|$$
logを外すために左辺と右辺でわけます。
$$log|zx|=-u+C' (C'=-C)$$
\(log\)を外して、
$$zx=e^{-z+C'} = C''e^{-z}$$
ここで\(z=\frac{y}{x}\)を代入して
$$y=C''e^{-\frac{y}{x}}$$
\(y≠0\)としていましたので、\(y=0\)となるような\(C‘’=0\)を含むような定数を\(C_1\)すると、
$$y=C_1e^{-\frac{y}{x}}$$
これが一般解となります。
同次形の式の見極め方
解き方はわかるんだけど、同次形の式ってどうやったらわかるの?


いくつか同次形のパターンへもっていく方法があるので、それを覚えた方がいいね。
そもそも同次形って何??っていう方もいらっしゃると思いますので、簡潔に説明します。
ここの微分方程式で間違いやすいのは、
同次形多項式と、同次形の微分方程式の解法で出てくる同次形は別物
です。
同次多項式 = 式のそれぞれの項の次数が同じモノ
これを人によっては同次形といったり、斉次(せいじ)形と言ったりします。
斉次という言葉は、微分方程式を習い始めたころから少しずつ出てくる言葉です。
『斉次』 = 『同次』 と置き換えましょう。
同次微分方程式、非同次微分方程式については下記の記事を参考にしてください。
具体例
同次多項式だけでは同次形にならない
\(x\)と\(y\)の関数として、\(f'(x,y)\)というものを考えます。
$$f'(x,y) = x^2 + 2xy + y^2$$
それぞれの項の次数は全部2次です(\(xy\)は[\(x\)の1次]+[\(y\)の1次]で2次です)。
これは2次の同次多項式ですが、同次形の微分方程式の解法で扱った形にはなりません。
$$(右辺) = \frac{1}{x^2}(1+\frac{2y}{x}+\frac{y^2}{x^2})$$
先頭に\(\frac{1}{x^2}\)があるので、同次形にはなりませんね。
同次形が使えるケース①
では、どういう形であればよいのか?
分母と分子が同じ次数の同次多項式の分数であれば、同次形の微分方程式の解法が使える可能性があります。
$$f'(x,y) = \frac{x^2}{x^2+xy+y^2}$$
$$f'(x,y) = \frac{x^3}{x^3+x^2y+xy^2+y^3}$$
などです。
これらは 分母と分子の次数が同じ同次多項式になります。
このケースであれば、 分母分子をxのn乗(nは多項式の次数)で割ってしまえば、同次形の微分方程式の形にできます。
同次形が使えるケース②
分母と分子の次数が同じ多項式でなければ使えないか、と言われればそうとは限りません。
分母と分子の次数が同じ同次多項式に、定数が入った形でも成立します。
簡単な例を示します。
$$f'(x,y) = \frac{x-y+A}{x+y+B}$$
\(X=x+x_0、Y=y+y_0\)とすると、\(\frac{dx}{dy}=\frac{dX}{dY}\)なので
$$f'(X,Y)=\frac{X-Y+\color{red}{x_0-y_0+A}}{X+Y+\color{red}{x_0+y_0+B}}$$
このまま定数項があると、同次形にもっていくことはできません。
というわけで、定数項を消去するように、\(x_0\)と\(y_0\)を決めます。
$$\color{red}{x_0-y_0 =-A}$$
$$\color{red}{x_0+y_0 =-B}$$
この連立方程式を解きます。
$$x_0 =\frac{-A+B}{2}、y_0 = \frac{A-B}{2}$$
このように\(x_0、y_0\)を定めると、定数項の部分を消去できます。
このとき、下記のような式になります。
$$f'(X,Y)=\frac{X-Y}{X+Y}$$
これで、\(X、Y\)の同次形の微分方程式として解くことができます。
ちなみに、定数項をつけても大丈夫か?という疑問がありそうですが、大丈夫です。
置き換えたときに微分したところがそのままでよいのか、という点が不安ですよね?
数式的に見てみましょう。
$$\frac{dY}{dX} =\frac{dY}{dy}\frac{dy}{dx}\frac{dx}{dX}$$
無理やり\(\frac{dy}{dx}\)を出して、\(\frac{dY}{dy}\)と\(\frac{dx}{dX}\)を計算してみましょう。
\(x=X-x_0、Y=y+y_0\)なので、下記のように計算しますね。
$$\frac{dY}{dy}=1$$
$$\frac{dx}{dX}=1$$
よって、
$$\frac{dY}{dX} =\frac{dy}{dx}$$
定数項を付けても大丈夫、ということですね。
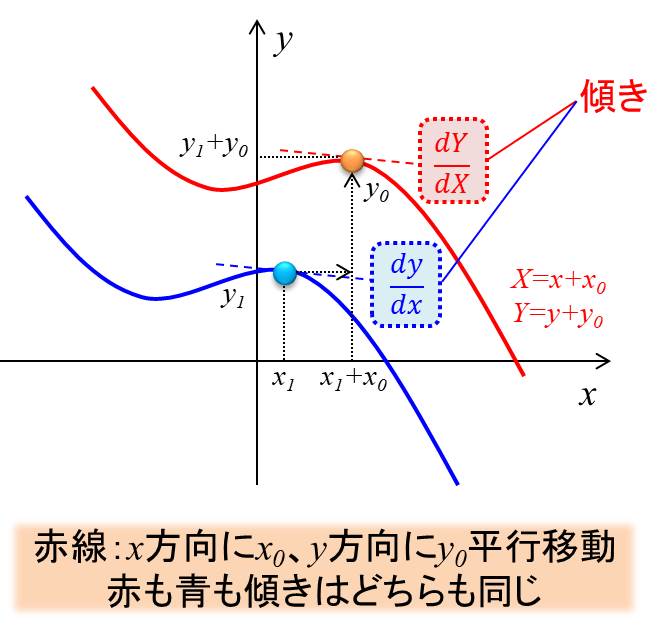
これはグラフでイメージしたほうが分かりやすいと思いますので、さらに補足します。
\(x\)と\(y\)に定数項をつける、というのは、グラフの形はそのままで、\(x\)と\(y\)方向に平行移動させる、ということです。
\(\frac{dy}{dx}\)や\(\frac{dY}{dX}\)がグラフ上で示すのは、その点における傾き、ですね。
平行移動させても、関数の形は変わらないので傾きも変わらない、ということです。
まとめ
本記事では微分方程式の同次形の解法について解説しました。
同次形の解法は下記の5ステップで解けます。
解法5ステップ
- \(\frac{y}{x}=z\)と置きます。
- \(y=zx\)、\(y'=z'x+z\)とします(式変形と微分するだけ)
- 元の式を\(z'x+z=f(z)\)と置き換える。
- \(z'=\frac{dz}{dx}=\frac{1}{x}(f(z)-z)\)と式変形する。
- \(f_1(x)=/frac{1}{x}、g(z)=f(z)-z\)として、変数分離形で解く
\(\frac{y}{x}=z\)と置くことと、そもそも同次形の式であることに気づくことが重要です。
分母分子が同次多項式で、次数が同じケースや、同次多項式でなくても、定数がついているだけのケースであれば同次形にもっていくことが可能です。
見切るためには、多少の慣れも必要ですので、しっかりと自分の手も動かして身に付けることを忘れないでくださいね。
