振動って苦手だなぁ…高校のときも振動のところよくわからかったし…調和振動子って言葉出てきたんだけど、いったい何なの?

本日は、振動・波動の基礎として単振動(調和振動子)と振動の基礎用語について説明します。
レベルとしては高校3年生向けくらいで解説します。
ちなみに、調和振動子は古典力学と量子力学で少し表記が違います。
今回は高校物理の範囲なので、古典力学的の範囲で解説します。
動画でも解説していますので、参考にしていただければと思います。
単振動(調和振動子)とは
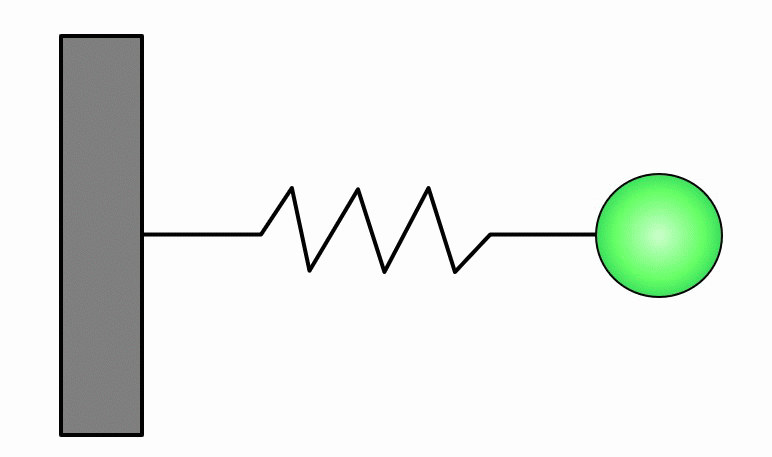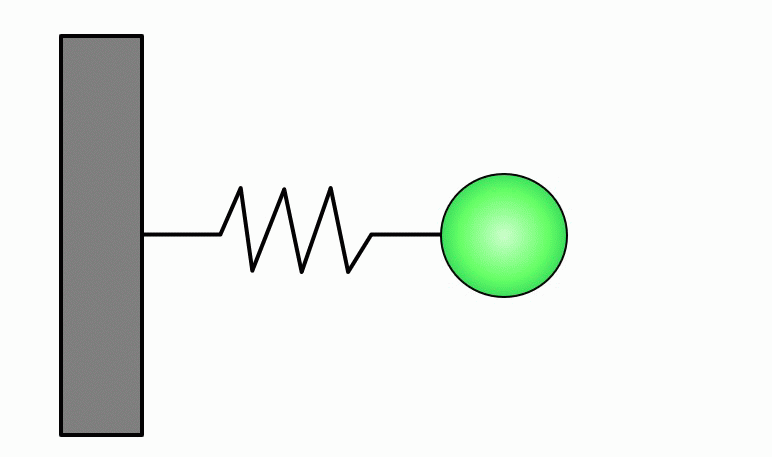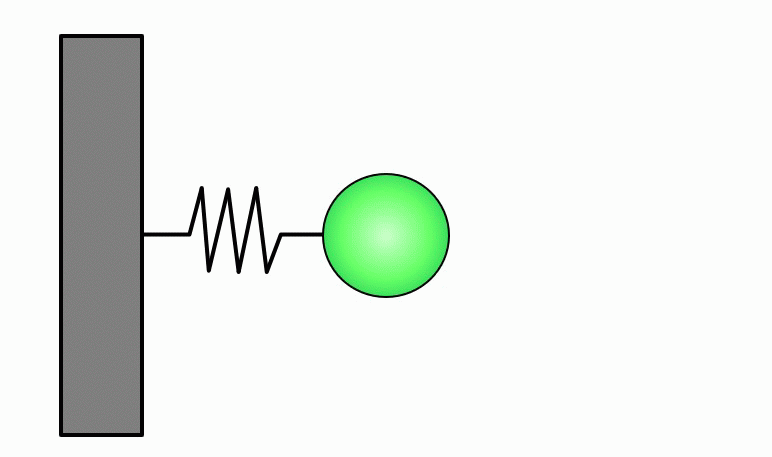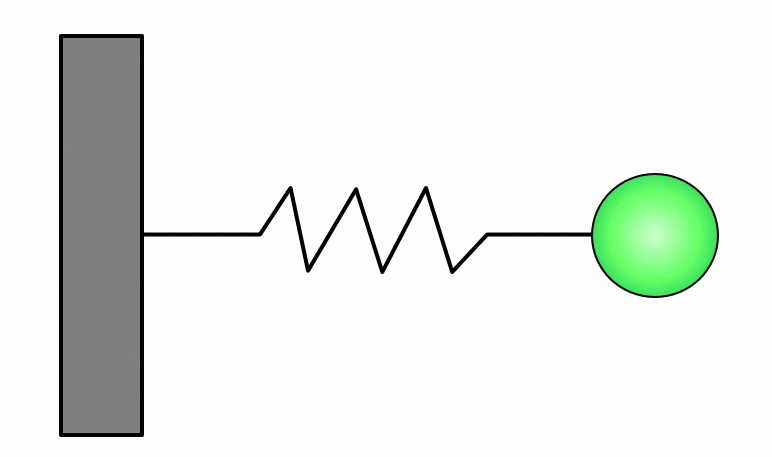
単振動(調和振動子)の概念
調和振動子 = 理想的なバネにつないだ時の振動
調和振動とは単振動と同じ意味で、調和振動子は調和振動するモノ、単振動するモノと覚えてください。
理想的なバネというのは、フックの法則に従うものです。下記の図のような状態ですね。
※物体と床の摩擦などは無視しています
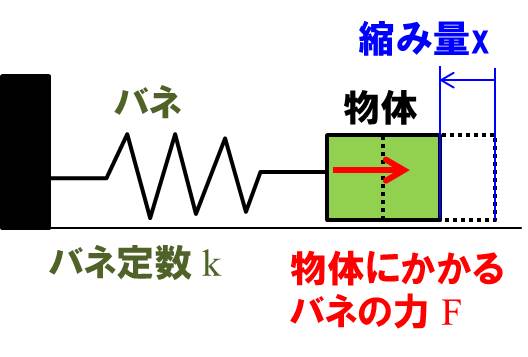
$$F=k×x$$
調和振動(単振動)の変位の式
どのような式に従うかについては下記です。
$$x = Asin(ωt+Φ)$$
結論として 三角関数で表されます。
横軸を時間\(t\)、縦軸を変位\(x\)としたグラフは下記のようなグラフになります。

時間とともに上下に波打って変位しているのがわかりますね。
え?変位の式にまだ説明していない文字が含まれている??
安心してください、これから振動の基礎用語を復習していきますので、そこで理解していきましょう。
振幅、周期、周波数について

振幅\(A\)
振幅は振動の大きさを示しており、上図の左側のグラフのように、0からの波の高さを振幅\(A\)で示します。
周期\(T\)
周期は1回振動するのにかかる時間であり、上図のグラフで赤色の波の部分を1回の振動と数えます。
この1回振動するのにかかった時間が周期\(T\)となります。
周波数\(f\)
次に周波数ですが、1秒間に振動する回数を示しています。
実際にグラフで数を数えてみましょう。
下のグラフは1秒間に2回振動しているので、2Hzのグラフになります。

次に5Hzのグラフを見てみましょう。

先ほどより早いスピードで振動しているのがわかると思います。
周期と周波数の関係
振動の周波数\(f\)は、振動の周期\(T\)の逆数です。
$$ T = \frac{1}{f} $$
これはよく使うので暗記しておいた方が早いです。
角振動数ωについて
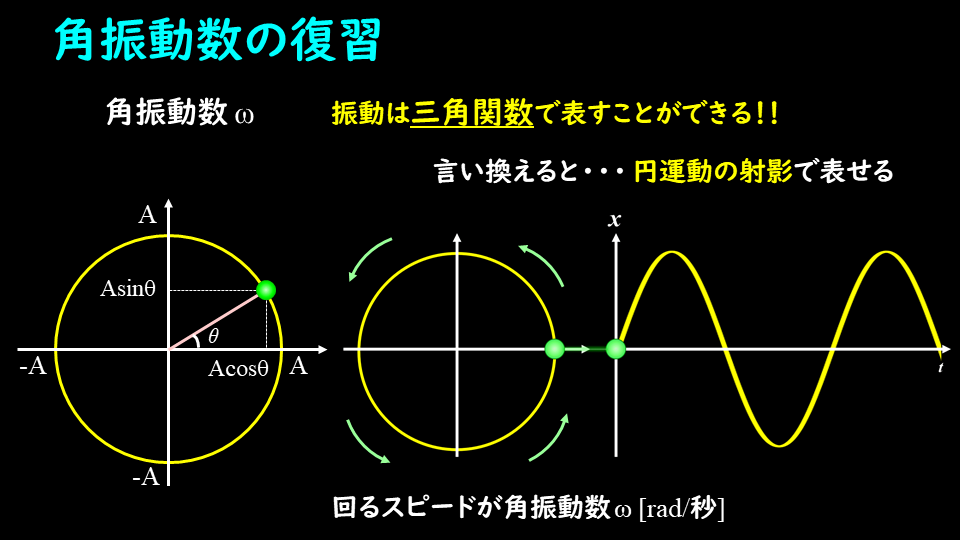
角振動数についてですが、振動は三角関数で表すことができるので、これを言い換えると、
振動の変位は円運動の射影で表すことができる
と言い換えることができます。
等速円運動の射影とはすなわち、円上の物体の\(x\)座標もしくは\(y\)座標を表すので、これらも振動の変位の式と同じ三角関数となります。
この等速円運動の回るスピードが角振動数ωに相当し、単位は[rad/秒]となります。
角振動数ωは下記で示されます。
$$ω = 2\pi f$$
ωは振動の周波数に比例していますので、『 どれくらいの速さで振動しているか』、を示しており、物理的には周波数と同じ意味となります。
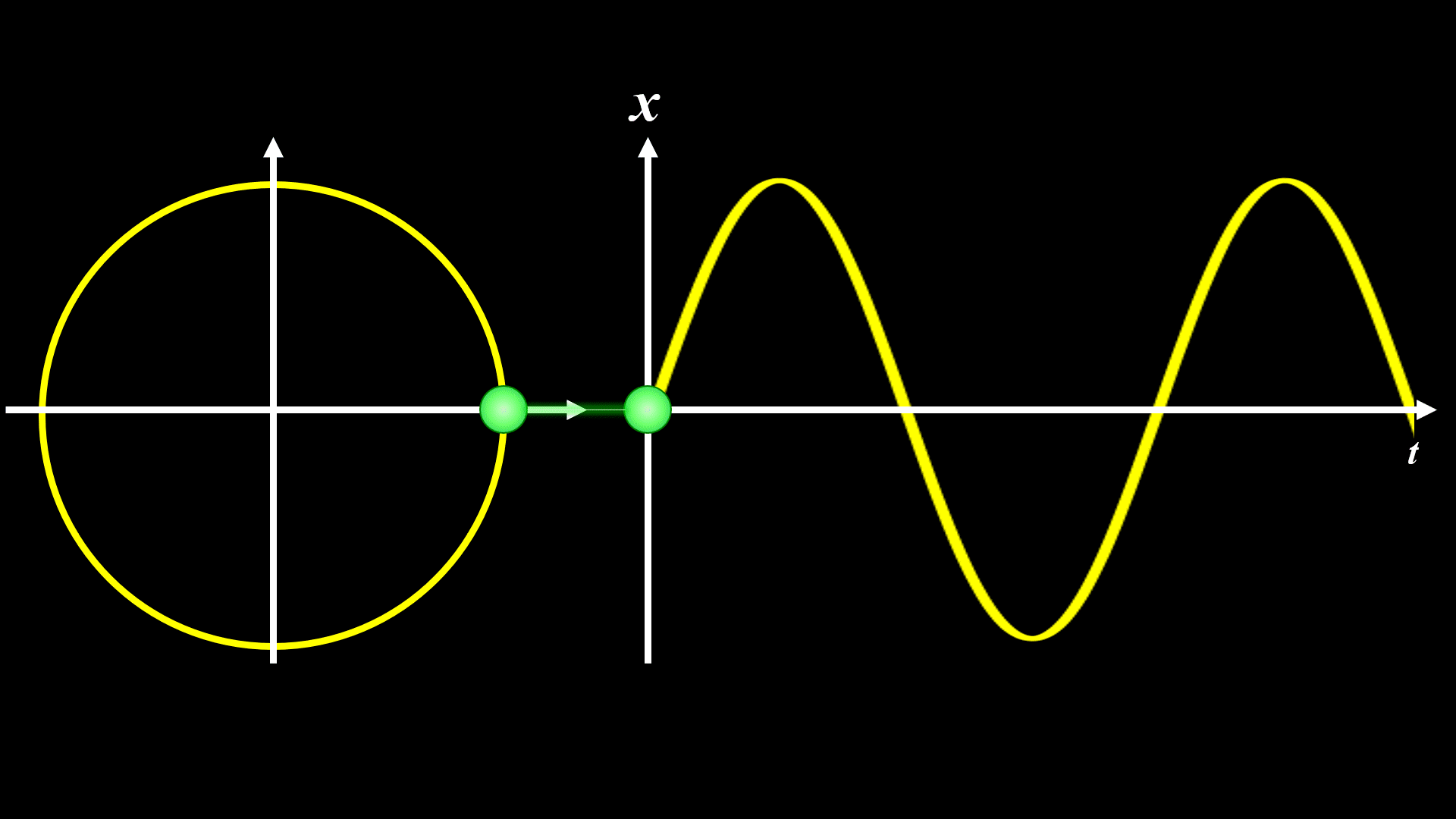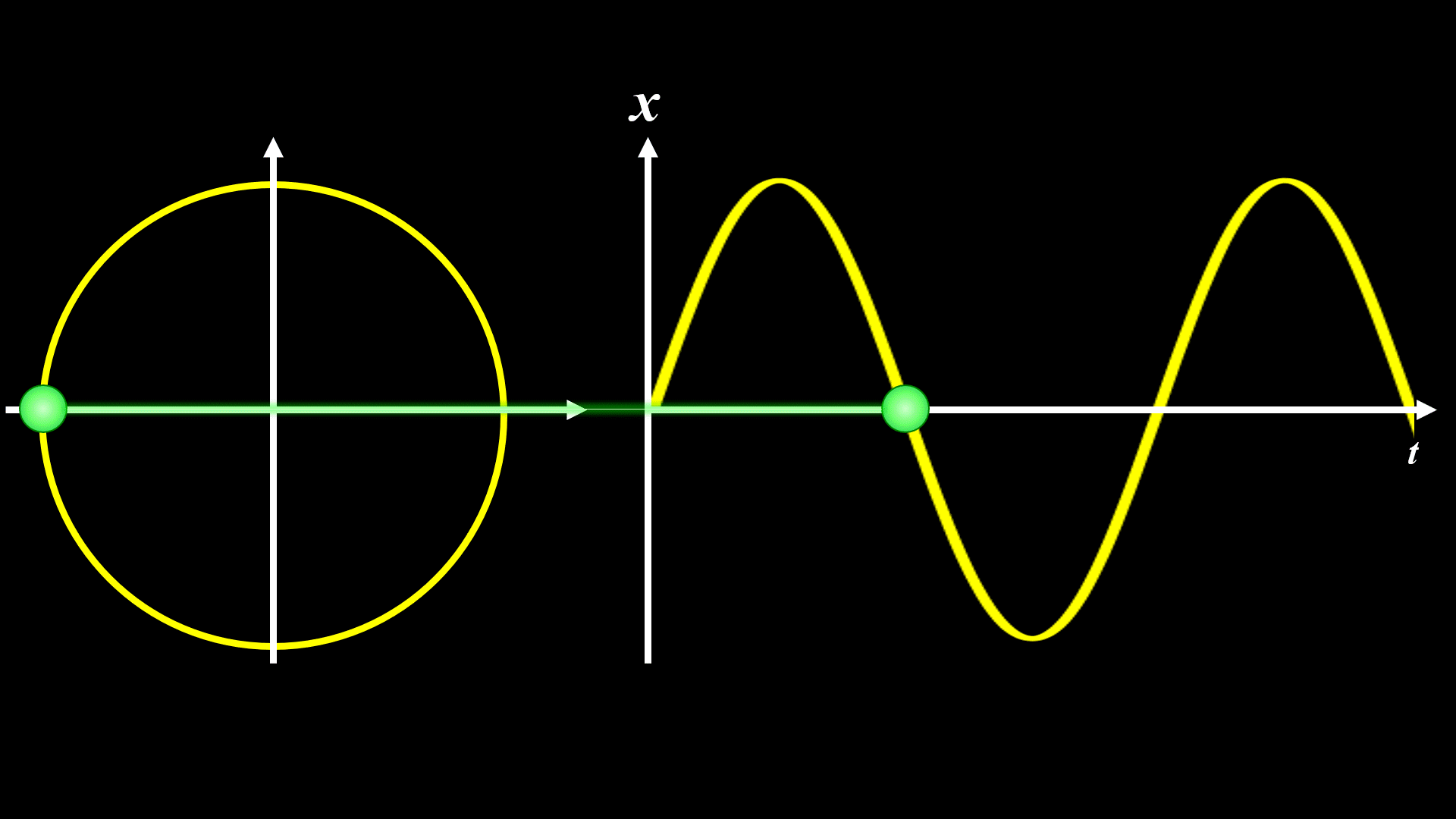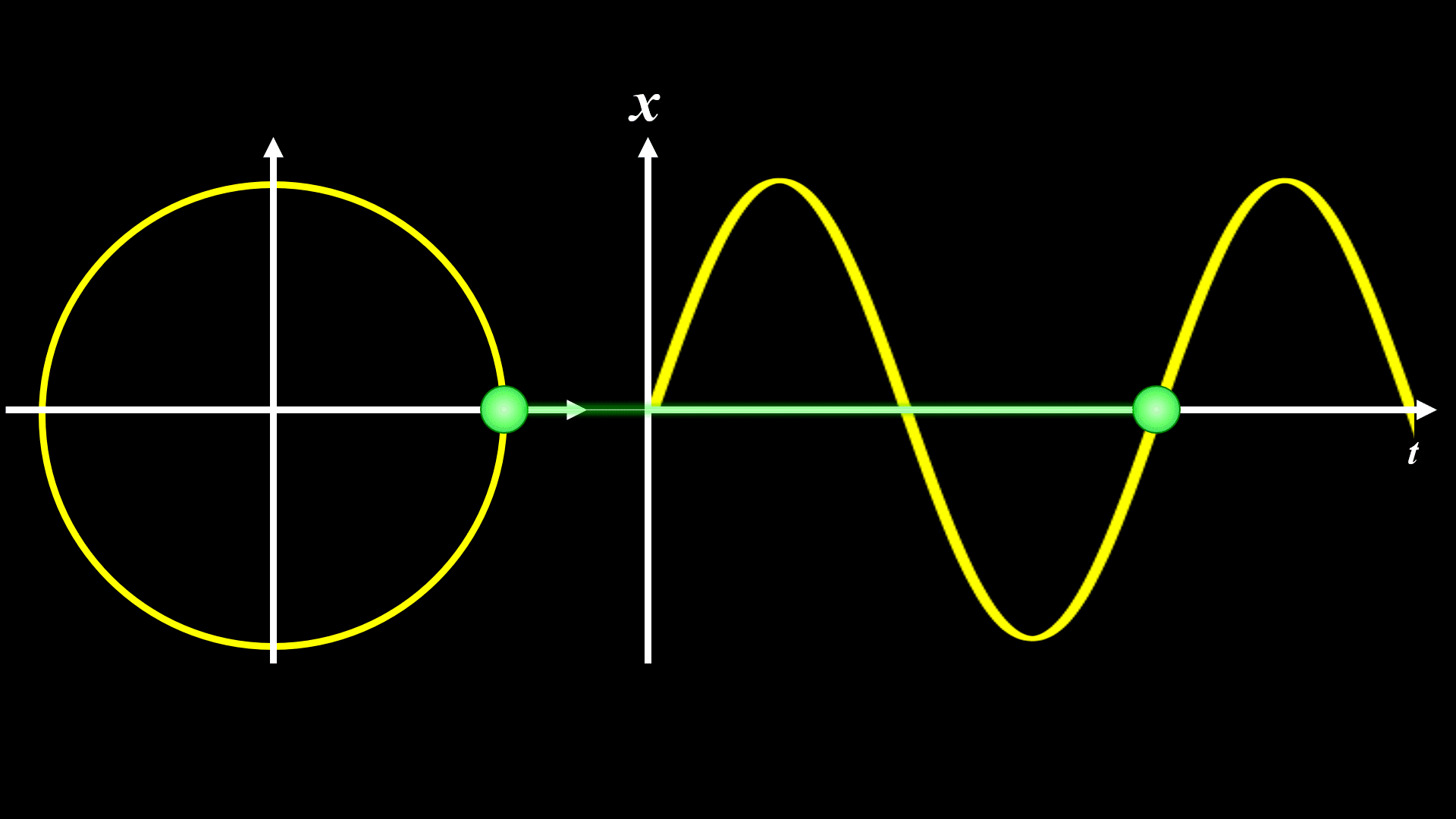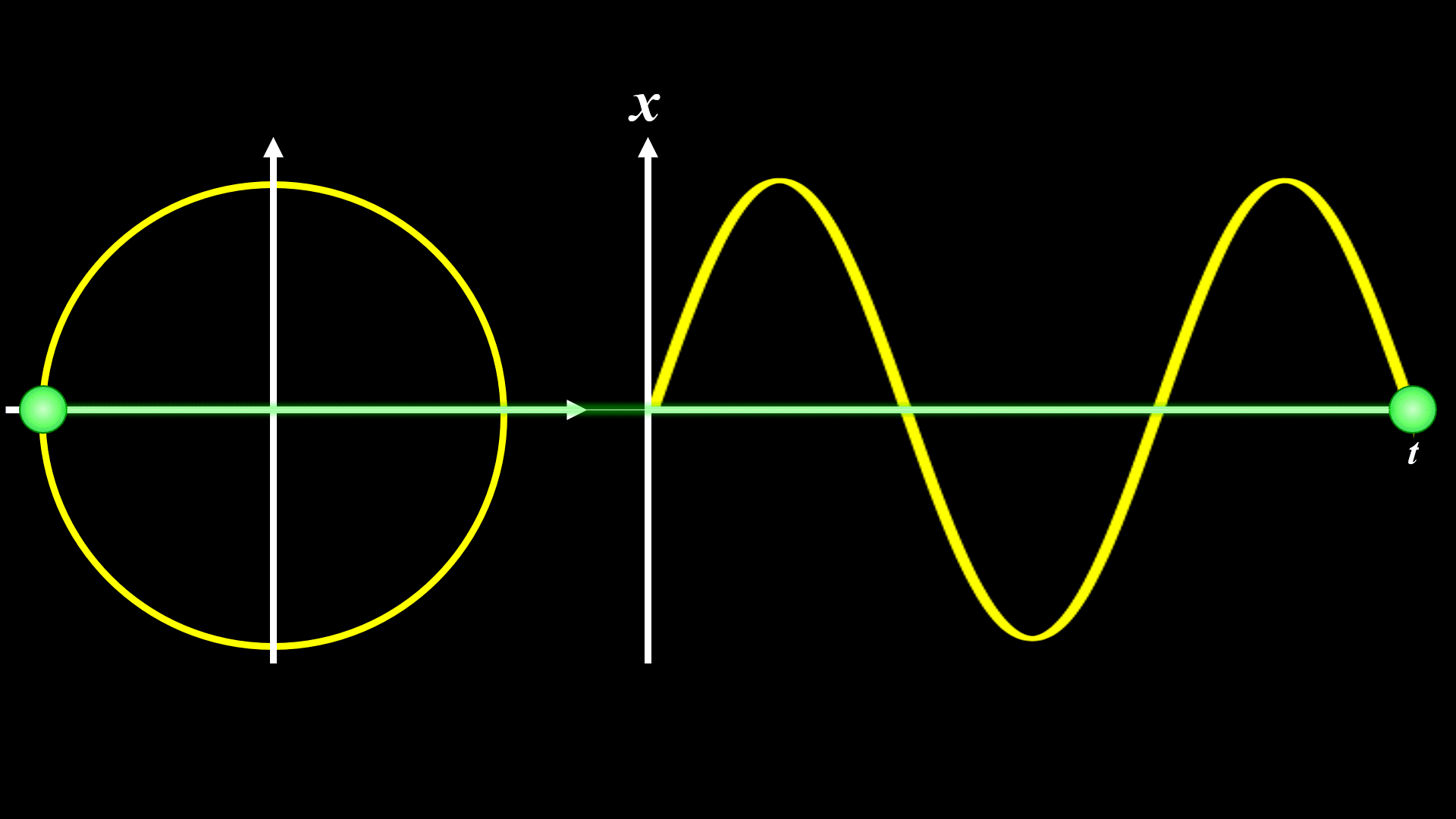
ωを倍にすると下記になります。
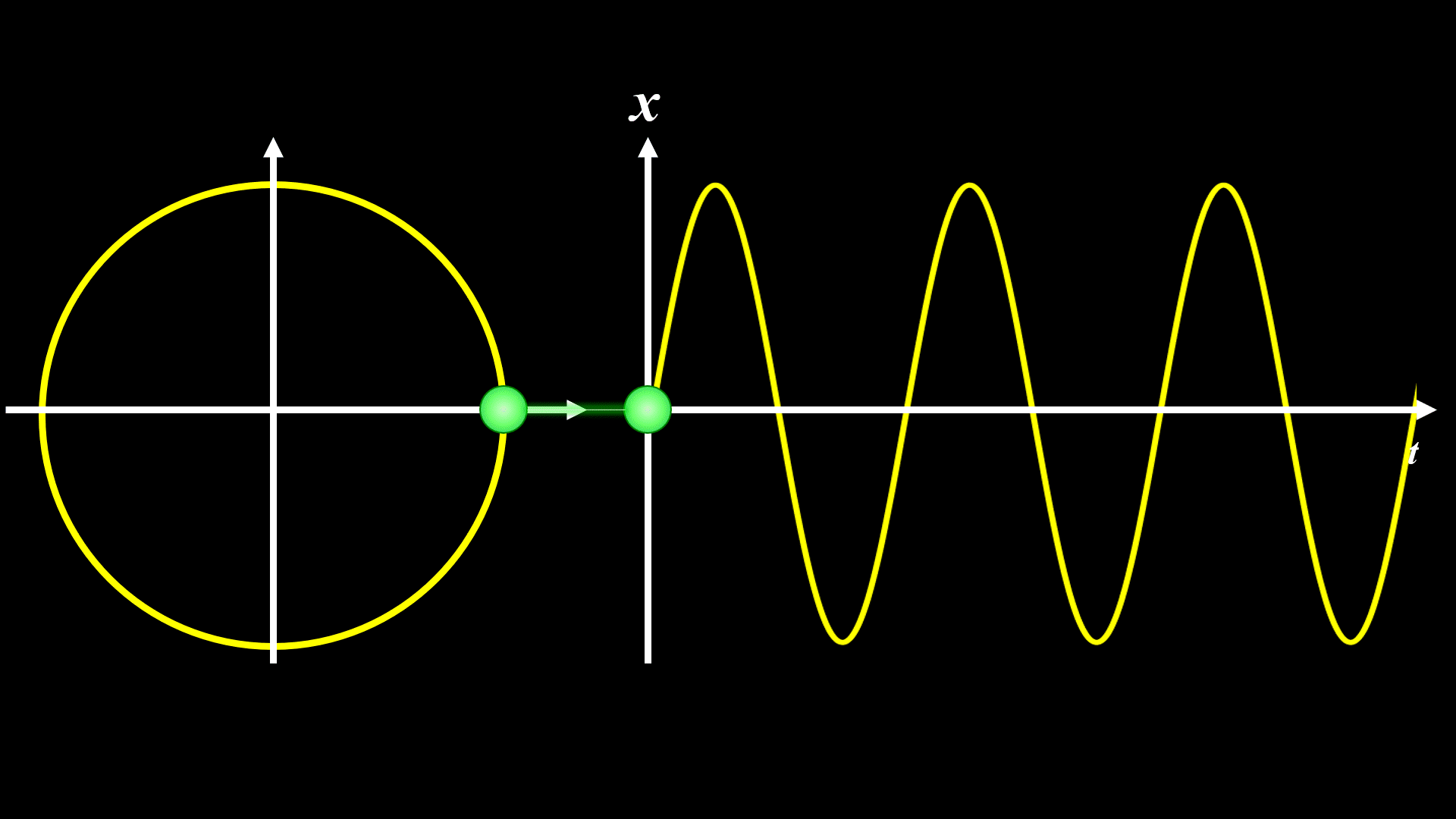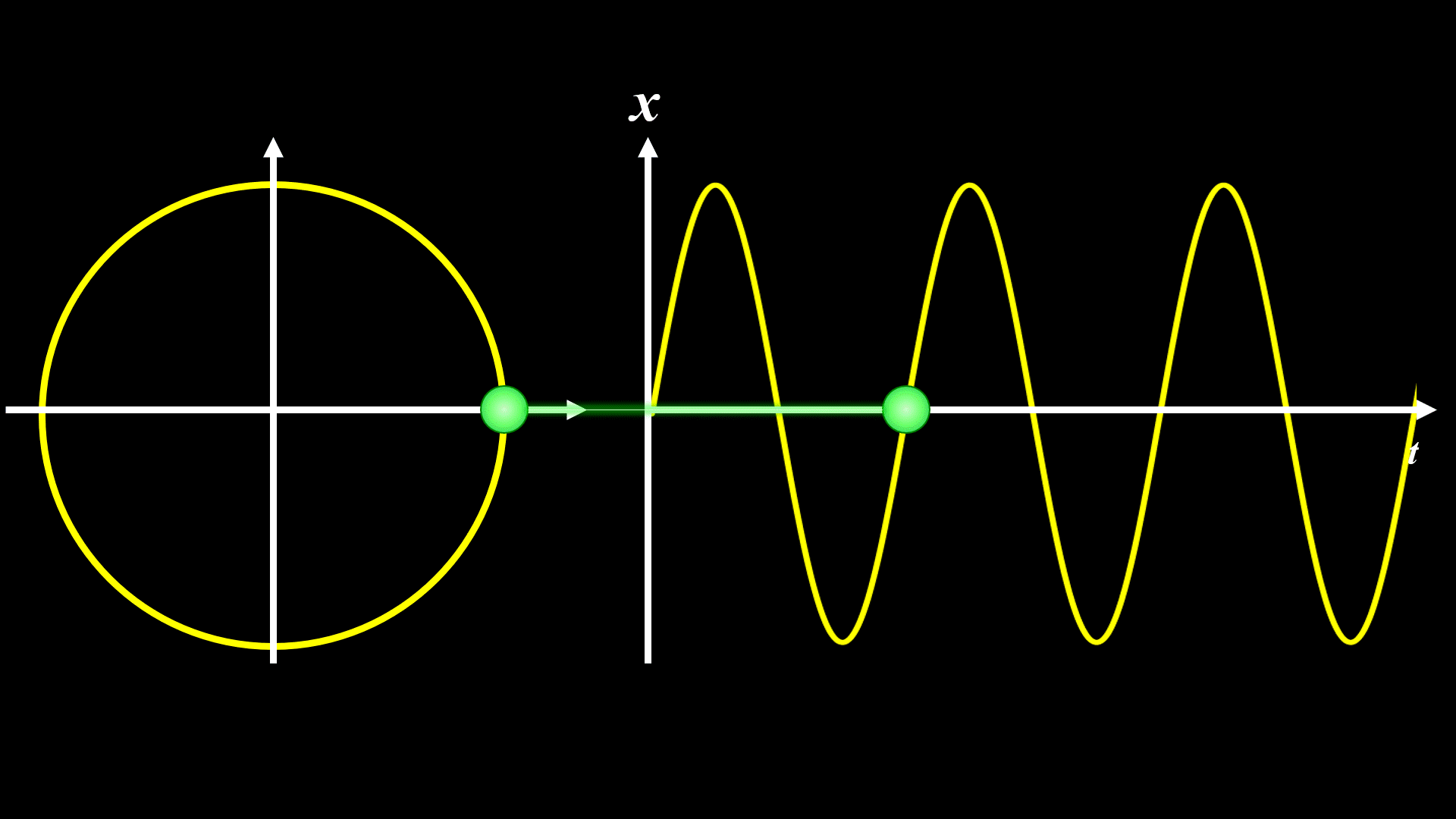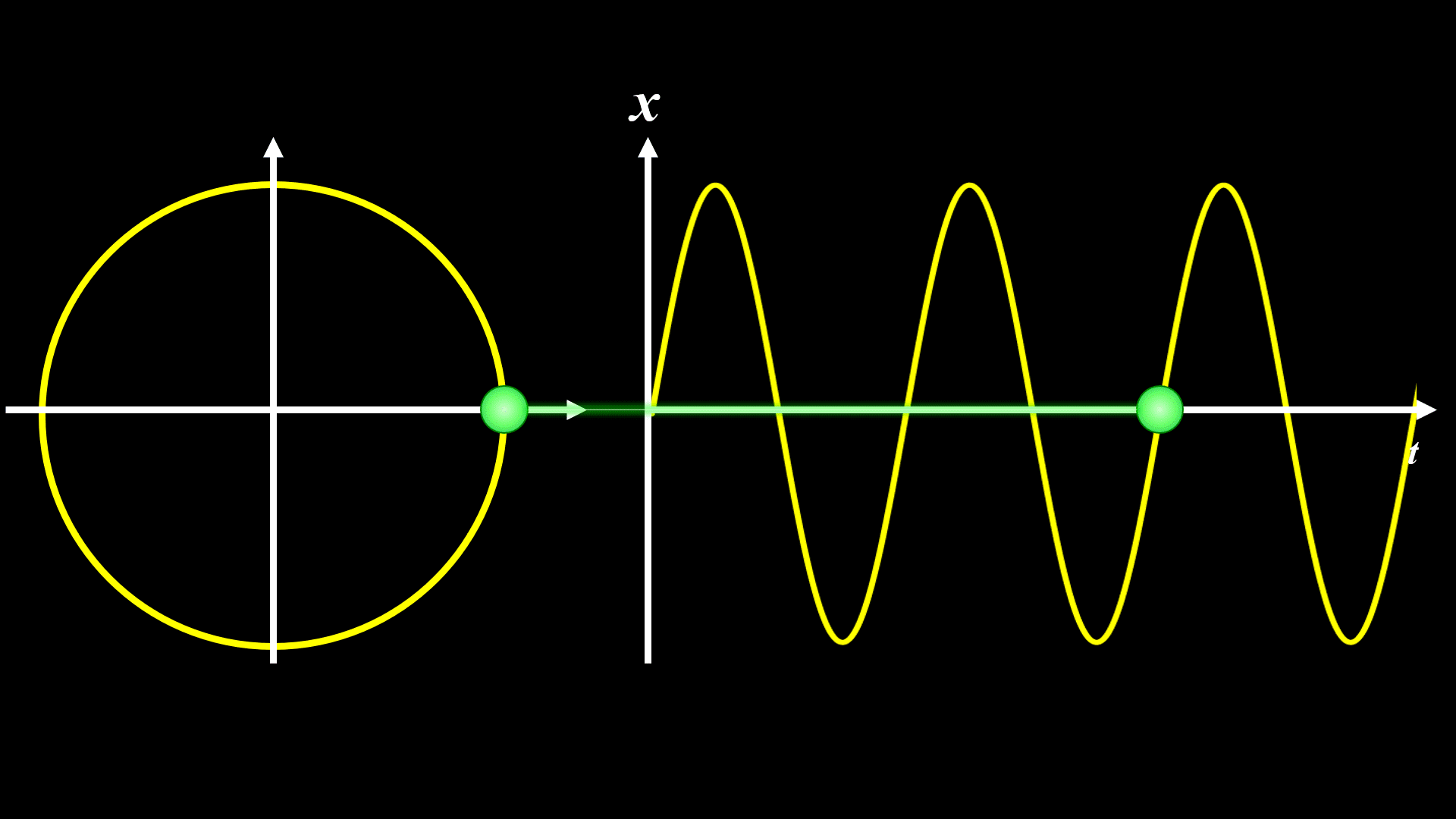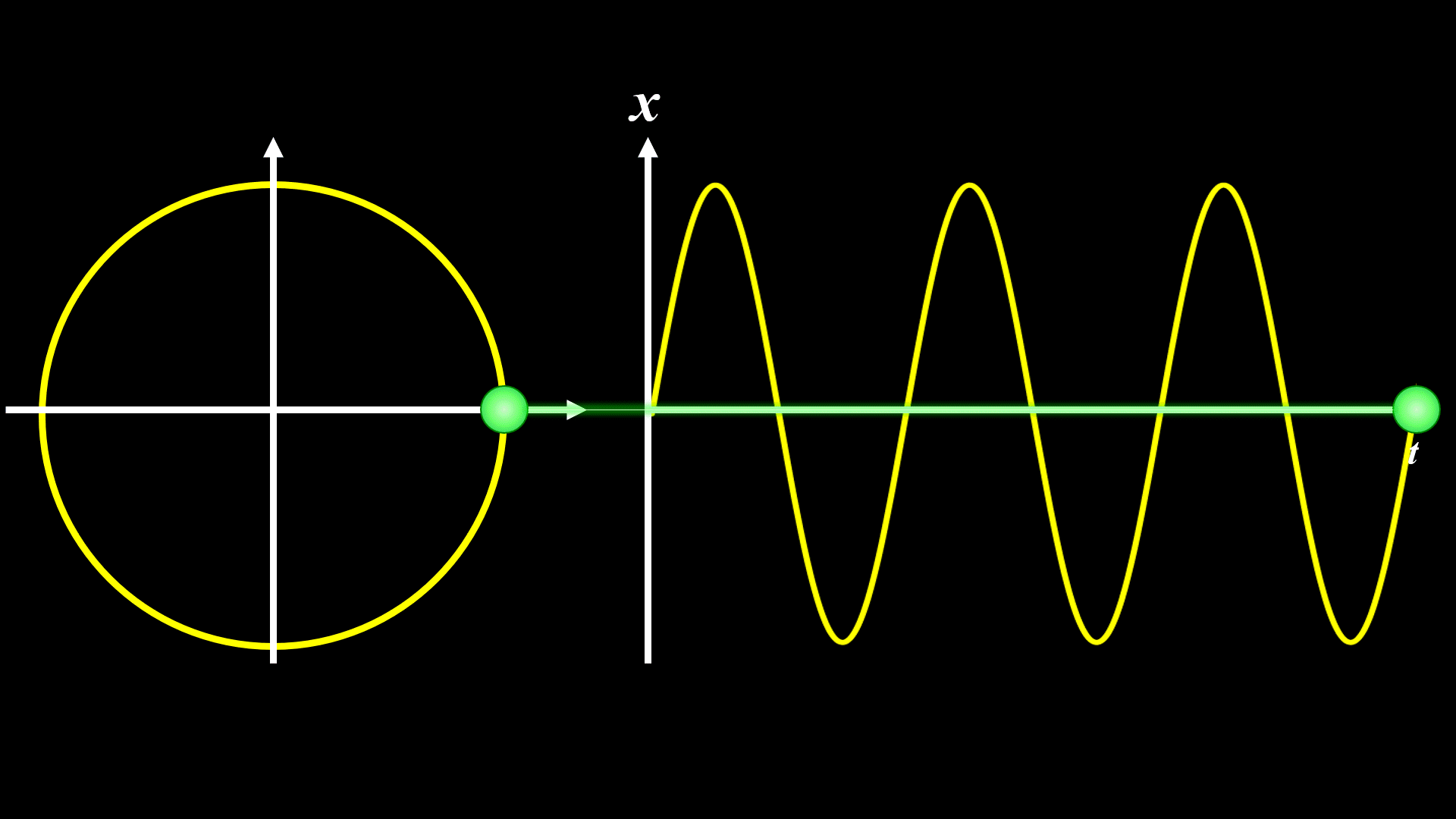
現実には重力が働いていたり、空気抵抗があったりするので、厳密にはこのようなアニメーションのようになりません。
あくまで 理想的にはこのアニメーションのようになる、と考えてくださいね。
角振動数ωのイメージ
さて、ここで角振動数ωというパラメータの概念を説明します。
ωは振動の周波数に比例する値です。
どれだけの速さで振動するか、を示します。
バネの場合、ωは下記のような式になります。
$$ω = \sqrt{\frac{k}{m}}$$
\(k\)はバネ定数、\(m\)は物体の質量です。
角振動数ωのイメージ
- \(k\)について 硬いバネの方が速く振動するイメージ
- \(m\)について 軽い方が速く振動するイメージ
このイメージは超大切なので覚えておきましょう。
初期位相Φ
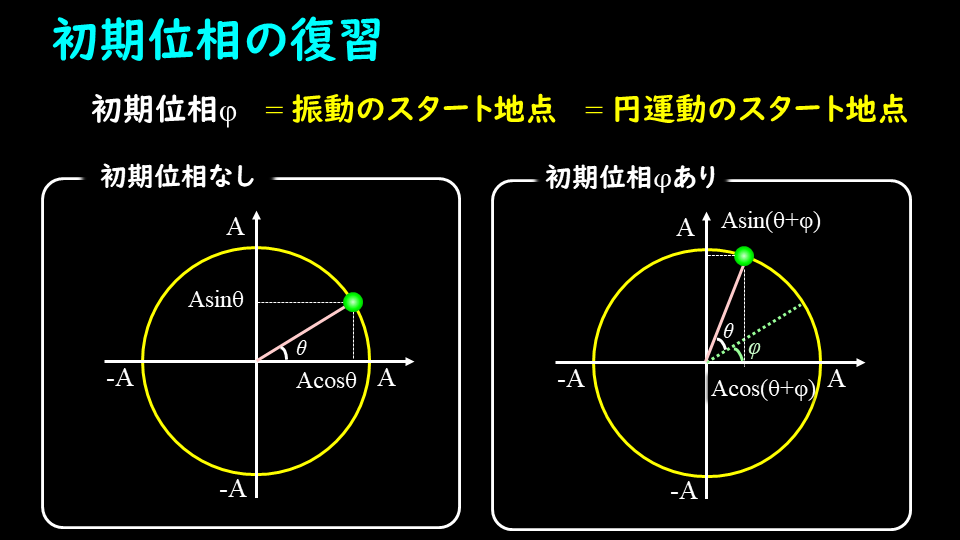
初期位相の話を無視してきましたので、ここで説明します。
初期位相は振動のスタート地点を示しています。
等速円運動で考えるとわかりやすいのですが、円運動のスタート地点と全く同じです。
今、物体の最初の位置を\(x=0\)としてきました。
これがゼロでない場合、初期位相が必要となってきます。
具体的には下記のグラフで説明します。
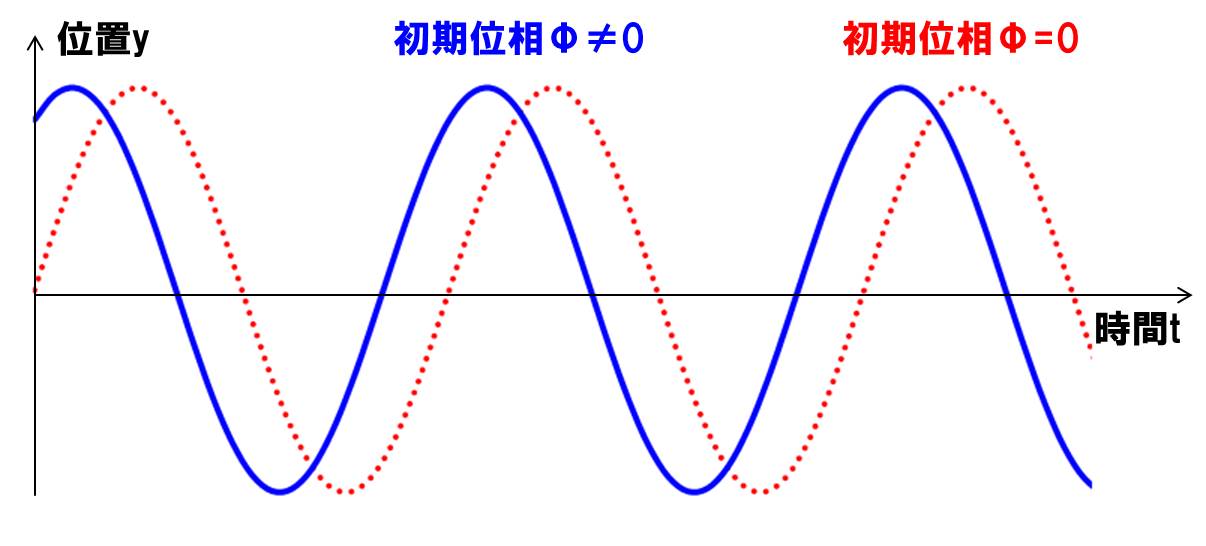
青の線が初期位相がある場合、赤の線が初期位相が無い場合です。
青の線では、物体の最初の位置が変わっている(\(y≠0\))となっています。
また、初期位相があることによって、波形が横方向にスライドしたように見えますね?
これを位相がずれる、と表現したりします。
初期位相の分だけ、波形がずれるんですね。
よく高校物理とかで、\(sin\)型とか\(cos\)型とかで説明されると思いますが、実用性は皆無です。
\(sin\)型で初期位相90°とすると\(cos\)型になるんですから、\(sin\)型、\(cos\)型という分類をするのがそもそも無駄です。
初期位相というのは、物体の最初の位置を合わせるためのパラメータと覚えてください。
速度と加速度について
これらは、変位の式を微分していくことで求まります。
変位の式は前述した通りで下記です。
$$y = Asin(ωt+Φ)$$
これを\(t\)で1回微分したものが速度\(v\)、2回微分したものが加速度\(a\)ですね。
グラフで重ねると下のようになります。(ω=1としています)
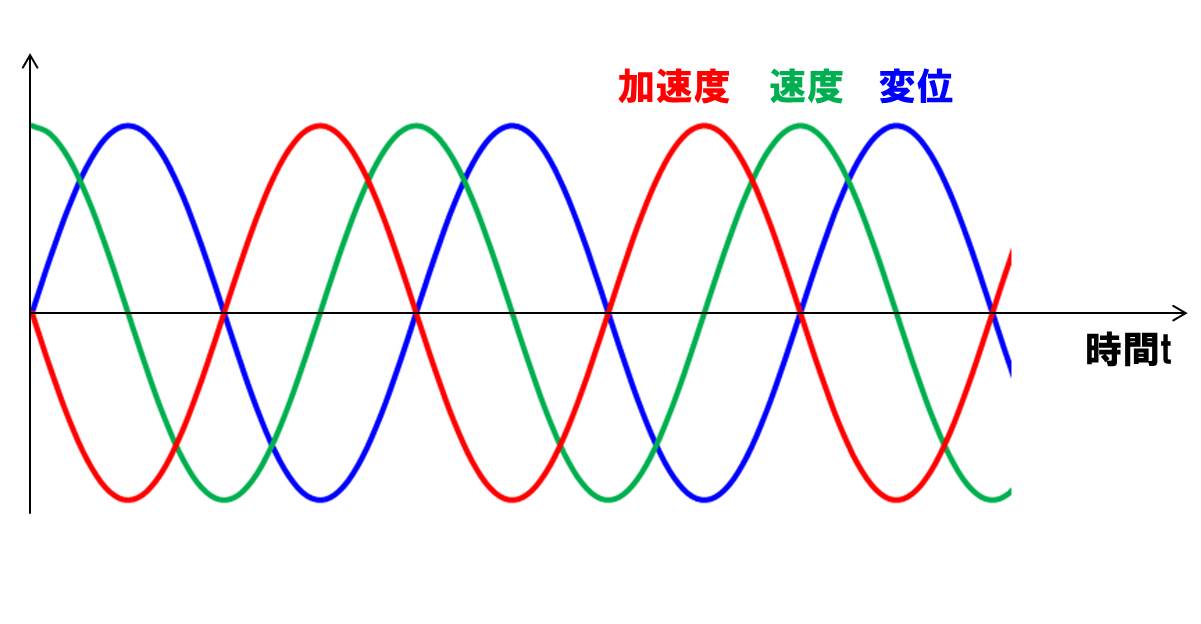
少し見づらいですが、このような感じになるという感覚だけもっておきましょう。
振幅の数値自体はωが入ってくる分、変位、速度、加速度で変わってきますので注意してください。
まとめ

調和振動子(単振動)について解説しました。
根本的には古典力学も量子力学も考え方としては同じなので、基礎的な内容を本記事でイメージをもっていただければ応用が利きます。
調和振動とは、理想的なバネの法則 フックの法則での振動で、三角関数で変位、速度、加速度は表されます。
これらの振幅は周波数によって変わってくる、ということを注意点として覚えておきましょう。
そして、この調和振動というのは理想的な状態である、ということも意識しておいてください。
現実には減衰であったり、非線形効果などが効いてくるため、この理想状態から違う結果となります。
このあたりは別記事で解説していますので、参考にしていただければと思います。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 振動・波動:小形正男、裳華房
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
