授業で急に非線形って出てきたんだけど、いったい何なの??

初学者に向けて、わかりやすく非線形、特に非線形の振動というものを解説します。
この記事では、できるだけ数式を使わず、イメージがわかるように説明していきます。
今まで何のこっちゃさっぱりだった人にも、この記事を読めばイメージをつかんでいただけます。
非線形とは
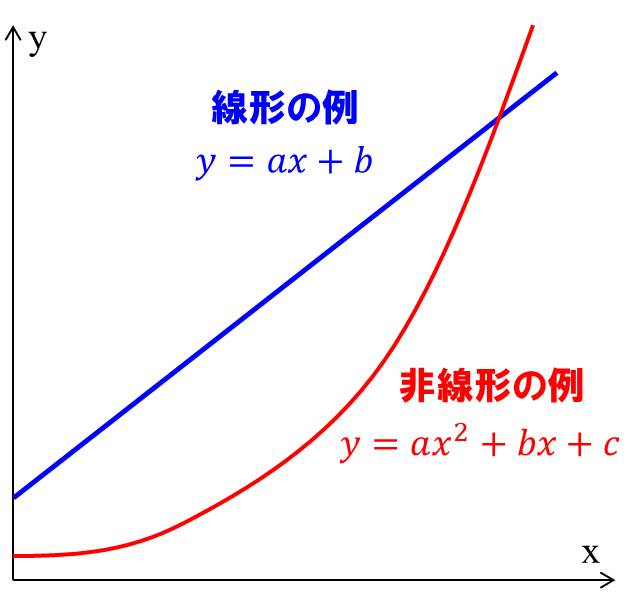
ざっくりと上図のように、 線形は1次関数、 非線形はそれ以外の関数で表されるもの、と覚えてください。
え?それだけ?という声が聞こえてきそうですが、それだけです。
線形と非線形の例を下記に示しますね。
線形の例
バネ:フックの法則
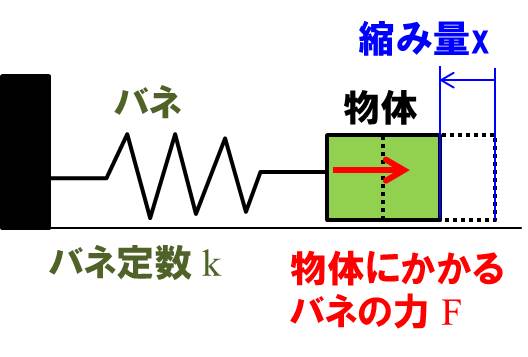
$$F=k×x$$
これは、バネの力は、バネの変位量(縮み量や伸び量)に比例する、ということを示しています。
比例する、というのは1次関数で表されるということになりますので、線形に変化する例となります。
オームの法則
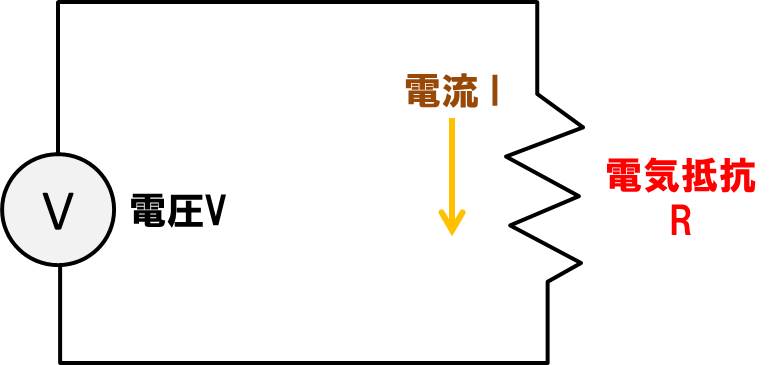
$$ V = I × R $$
かの有名な電気回路の公式、オームの法則も、電圧は抵抗、もしくは電流に比例します。
このように、シンプルで美しい物理現象には線形のものが多いのです。
非線形の例
線形ではないもの、なので実はめちゃくちゃ多いです。
数式も複雑なものが多いので、個別に詳細を書かず、下記にリスト化しますね。
非線形の例
- 気象情報(雲の動き):カオス現象と言われています
- ブランコ:身近ですが、非線形の力学で解析される現象です。
- LCR回路:電気回路でもコイルやコンデンサを入れると非線形の特性を示しますね。
- ダイオード:小さい電圧で大量の電流が流れ、そのI-V特性は1次関数の形から大きく外れます。
- 波の伝搬:三角関数で示されますので、これも非線形です。
- シュレーディンガー方程式:波動の方程式ですが、これは微分方程式ですので、非線形ですね。
挙げたらキリがないです。
ちなみに、線形と思われる現象というのは、理論的に1次関数に従う、ということなので、実際にやってみると線形でなく、非線形のような結果になるということも多々あります。
実験はなんでもかんでも理論的な結果が得られるわけではない、ということです。
非線形の振動
次に、非線形性があるモノが振動した場合、どのようなことが起こるかを説明します。
非線形の例として、次のような非線形の式を考えます。
$$F = k_1x ± k_3x^3$$
線形の例で示した、バネのフックの法則に$k_3x^3$を付け加えたような形です。
ちなみに両端固定梁とかはこの式の$k_3$の係数が+のケースになります。
詳しくは下記の記事を参考にしてください。
グラフを描くと下記のようになります。
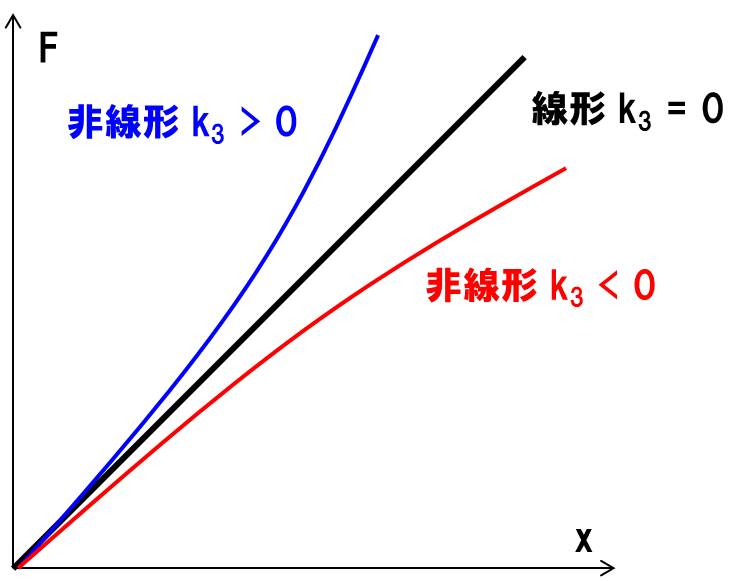
\(k_3\)が+のときをハードニング、-のときをソフトニングとも言います。
変位量が大きくなると、どんどん硬くなる(ハードニング)、もしくは軟らかくなる(ソフトニング)というイメージです。
こういう挙動を持つモノの振動特性はどうなるのか?
振動特性というのは、どんな周波数で、どれくらい振幅するか、ということを指します。
結論、下記のようなグラフになります。
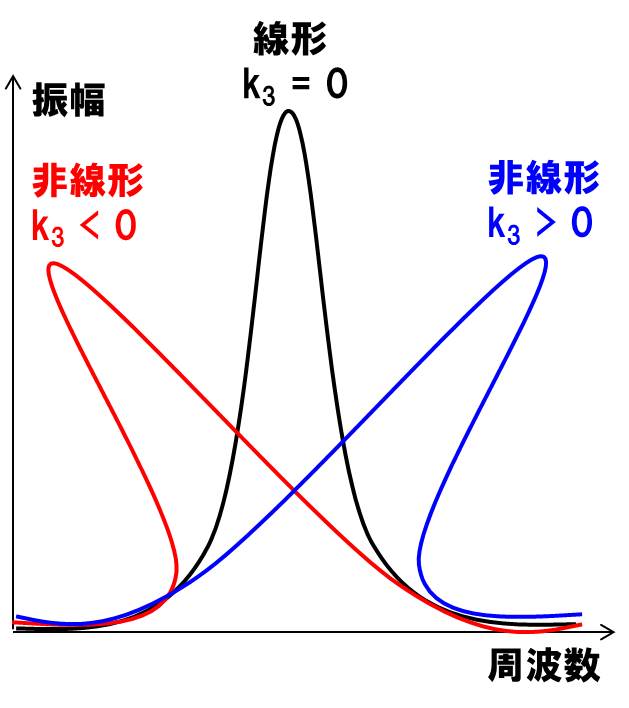
なんじゃこりゃ??と感じた人もいらっしゃると思います。
線形の時は、共振が発生する周波数で、共振ピークが鋭く立ち上がります(図の黒の線)
しかし、非線形にすると、図の青線や赤線のように、ピークがぐにゃりと曲がった形状になります。
曲がる方向は\(k_3\)の+と-で変わります。
んん??とある周波数では、振幅が3種類あるんじゃない?どうなってんの?

どういうことかを、下のグラフで示します。
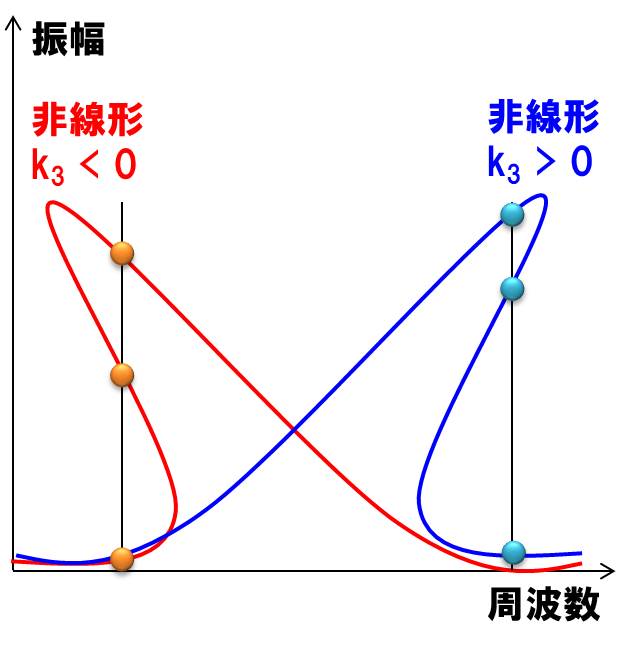
グラフにオレンジの点や、水色の点を追加しました。
これらは、同じ周波数なのに、違う振幅を3種類持つ、ということを示しています。
方程式を解くと3つの解をもってしまう領域なので、数学的にそうなっています。
では、実際にこの周波数の振動が加わった場合、どの振幅で振動するのか?
これは振動を加える直前の状態で決まります。
この周波数の振動を加える直前の状態が、止まっていたら、一番下側の振幅で振動します。
一方、直前の状態が、一番上側の近くの振幅で振動していたら、一番上側の振幅で振動します。
これらの性質から、非線形の振動は、周波数を低い側から高い側へ変化させたときと、
周波数を高い側から低い側へ変化させたときで、周波数特性が変わってしまいます。
具体的には下のグラフのようになります。
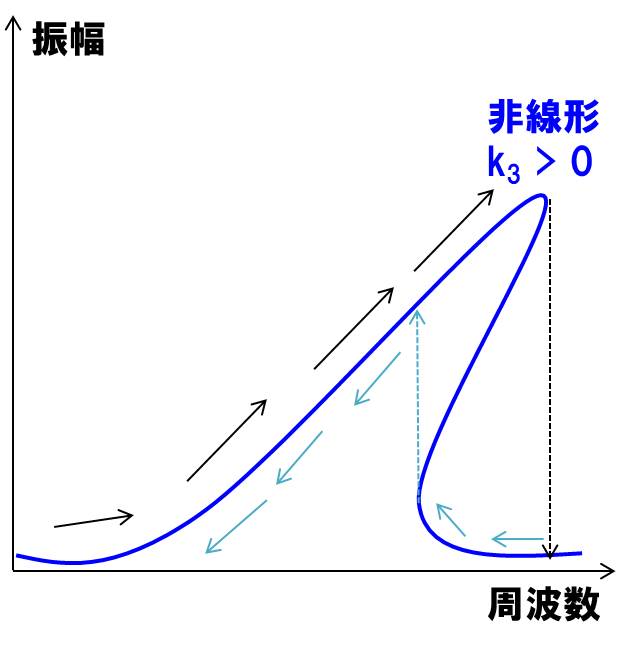
黒の矢印が周波数を低→高と変化させています。
水色の矢印が周波数を高→低と変化させています。
このような現象を履歴現象(ヒステリシス)と言います。
非線形振動の応用先は?
非線形振動は、このように面白い振動特性を持つのですが、では現実問題、どういったところで使われるのでしょうか?
よく聞く例としては、非線形にすることで、共振ピークの帯域幅が増加する、ということを活かしたデバイスに応用します。
加速度センサーや振動発電機などが一般的です。
線形の振動を利用すると、どうしても共振ピークが鋭く立ち上がるため、使用できる周波数が狭くなってしまいます。
広い周波数で対応するためには、このピークの鋭さを落として、太っちょのピークにする必要があるのですが、そうするとピークの高さが極端に落ちてしまいます。
ピークの高さを保ちつつ、広い帯域幅を実現するために、非線形を利用することがあるようです。
そのほかに、非線形振動の共振を防ぐ設計にするために、非線形振動の理論を解析する、ということもよく行われています。
ちなみに、今回紹介した非線形の式は、両端固定の構造物(橋など)の中央を上下に振動させたときの例に近い式になります。
(実際には、たわみを考慮したようなモデル化が必要です)
このあたりは今後、また記事で紹介させていただきます。
まとめ
非線形というものは何か、という説明をさせていただき、その例と非線形の振動について紹介させていただきました。
ざっくりとイメージはつかめたのではないでしょうか?
詳細の情報が知りたい方は、今後、さらに記事にしていきますのでご期待ください。
それではまた。
参考文献
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 非線形力学(共立物理学講座6):戸田盛和、渡辺慎介、共立出版株式会社
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
