変位型の振動の運動方程式が表記が違うんだけど…


以前解説した運動方程式の立て方は絶対座標系で、相対座標系で書いた場合と違うんだ。今日は相対座標系の内容を解説するね。
これまで変位型加振の運動方程式を絶対座標系で解きました。
振動・波動の基礎④-変位加振・地動加振・調和地動について 強制振動との違いも解説
教科書や大学の授業では絶対座標系ではなく、相対座標系で解いていることもあります。
求まる解としては絶対座標系と同じなのですが、相対座標系も理解しておき、どちらでも解けるようにしておきましょう。
動画でも解説していますので参考にしてください。
変位加振(地動加振)
強制振動とのモデルの違い
変位加振は、繋がれた質点に間接的に力を加え、振動させたときの状態を指します。
モデルを見て比較してみましょう。
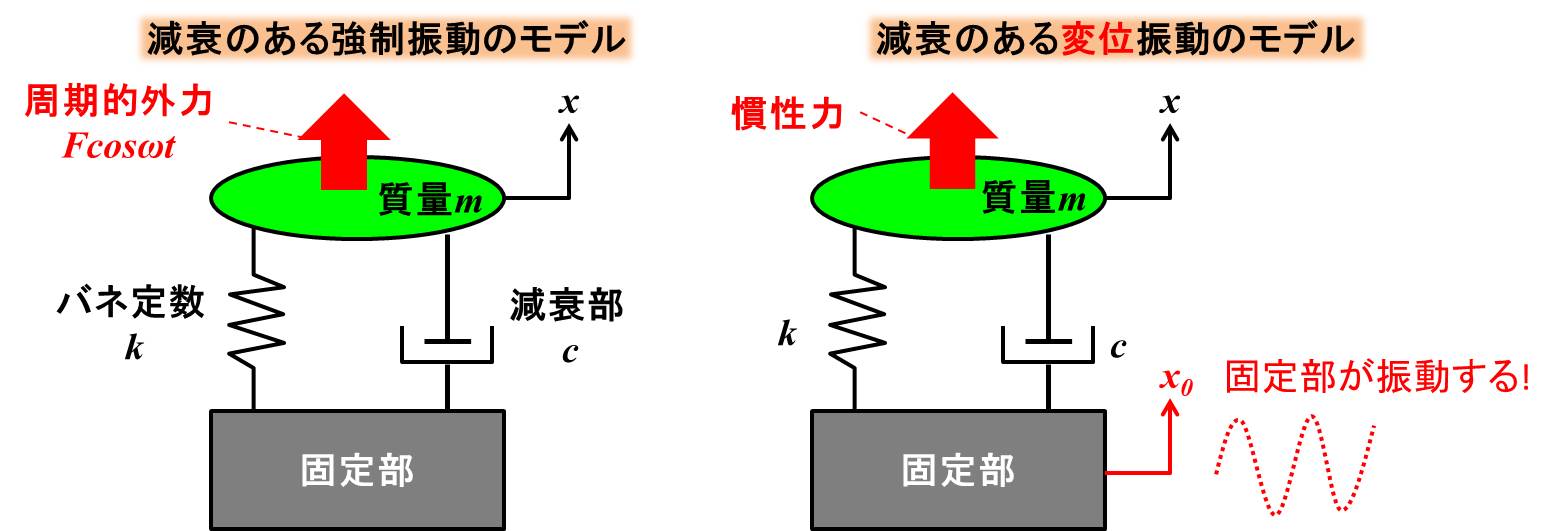
左側がこれまで扱ってきた強制振動のモデル、右側が変位振動のモデルです。
変位振動のモデルは固定部が揺れて、慣性力で質量を動かします。
この慣性力を考慮して運動方程式を作るのが、相対座標系です。

相対座標系の復習
相対座標系では下記のように慣性力を考慮する必要があります。

白い人からバスに乗っている青い人を見たとき、白い人がバスに乗っていない場合は、青い人は右側に動いているように見えます。
このときの運動方程式は、バスから青い人にかかる力を\(F\)とすれば下記のようになります。
$$ma=F$$
これは絶対座標系で見たときの運動方程式です。
一方、相対座標系の場合、白い人は青い人と同じバスに乗った状態で運動方程式を立てることになり、
白い人から見ると青い人は同じバスの中で静止しているように見えますね。
このときの運動方程式は、止まっている=加速度ゼロだから、左辺はゼロとなり、下記のようになります。
$$0=F-ma$$
この式の\(-ma\)が慣性力で、右辺の\(-ma\)を左辺に移項すると、絶対座標系と全く同じ式となり、
運動方程式の解は変わらないことがわかりますね。
運動方程式を立てる
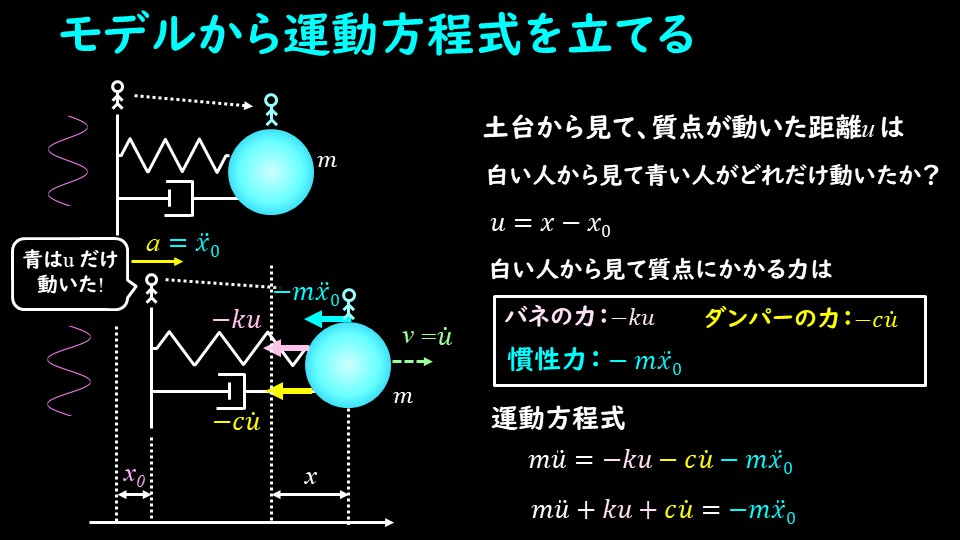
それではモデルから運動方程式を立ててみましょう。
図のように、土台に乗っている白い人から、質点に乗っている青い人を見たときの運動方程式を考えます。
まず、白い人から見て、青い人が動いた距離は、相対距離となります。
土台の変位量を\(x_0\)、青い人の変位量を\(x\)とすると、相対距離\(u\)は
$$u=x-x_0$$
となります。この相対距離分、バネやダンパーは伸び縮みしているので、バネの力、ダンパーの力はそれぞれ下記のようになります。
バネの力:\(-ku\)
ダンパーの力:\(-c\dot{u}\)
この二つの力に慣性力\(-m\ddot{x}_0\)を加えて運動方程式を書くと、
$$m\ddot{u}=-ku-c\dot{u}-m\ddot{x}_0$$
となり、左辺に\(u\)の項を、右辺に\(x_0\)の項を持ってきて整理すると、下記のようになります。
$$m\ddot{u}+ku+c\dot{u}=-\ddot{x}_0$$
運動方程式を解く

それでは運動方程式を解いていきましょう。
土台の変位\(x_0=Xsinωt\)として、運動方程式に代入すると、
$$m\ddot{u}+c\dot{u}+ku=mXω^2sinωt$$
となります。この運動方程式を複素数を用いて解いていきます。
複素数を用いた解法については過去の記事や、下記の動画を参考にしてください。
複素数を用いた解法の最初のステップですが、下記2つの式を作り、足し合わせます。
- 右辺=\(mXω^2cosωt\)の式を作る
- 右辺=\(mXω^2sinωt\)の式に複素数$i$をかけた式を作る
まず右辺=\(mXω^2cosωt\)の式は
$$m\ddot{u}+c\dot{u}+ku=mXω^2cosωt$$
となりますね。次に右辺=\(mXω^2sinωt\)の式に複素数$i$をかけた式は下記のようになります。
$$i(m\ddot{w}+c\dot{w}+kw)=imXω^2sinωt$$
ここで、座標を\(u\)から\(w\)に表記を変更しています。
単純に\(cos\)の式を作った際に\(u\)をすでに使ってしまっているので、代わりに\(w\)を使っただけですね。
さて、それではこの\(u\)の式と\(w\)の式を足し合わせます。
ここで、\(cosωt+isinωt=e^{iωt}\)というオイラーの公式を使って書き直すと、
$$m\ddot{u}+c\dot{u}+ku+i(m\ddot{w}+c\dot{w}+kw)=mXω^2e^{iωt}$$
となります。

ここでuとwが混在した形になっているので、\(u+iw=z\)とおくと、運動方程式は下記のように書き直せます。
$$m\ddot{z}+c\dot{z}+kz=imXω^2e^{iωt}$$
このように書き直すと、特殊解として\(z=Ae^{iωt}\)とおけば方程式を満たしそうですね。
実際に特殊解を代入して、係数Aを求めると下記のようになります。
$$A(-mω^2+icω+k)=mXω^2$$
ここで、両辺を\(m\)で割り、減衰比\(ζ\)と固有角振動数\(ω_0\)を用いて式を整理します。
$$ζ=\frac{c}{2\sqrt{mk}}$$
$$ω_0=\sqrt{\frac{k}{m}}$$
$$A(ω^2_0-ω^2+2iζω_0ω)=Xω^2$$
よって\(A\)を求めると、
$$A=\frac{Xω^2}{ω^2_0-ω^2+2iζω_0ω}$$
分母の複素数を実数にするために、分母分子に共役な複素数をかけて整理すると、
$$A=\frac{ω^2_0-ω^2-2iζω_0ω}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}Xω^2$$
この求めた\(A\)を特殊解\(z=Ae^{iωt}\)に代入して、
$$z=\frac{ω^2_0-ω^2-2iζω_0ω}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}Xω^2e^{iωt}$$

特殊解をもっと変形して、イメージがつく形にしていきます。
分子の部分を\(re^{iδ}\)の形で表して、\(e^{iωt}\)とまとめられるような形にします。
図の右側のように、複素数平面で考えたとき、分子は下記の\(r\)と\(δ\)を使って\(re^{iδ}\)の形に変形できます。
$$r=\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}$$
$$tanδ=\frac{2ζω_0ω}{ω_0^2-ω^2}$$
よって、下記のようになります。
$$z=\frac{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}e^{-iδ}Xω^2e^{iωt}$$
分母と分子は約分できて、
$$z=\frac{Xω^2e^{i(ωt-δ)}}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}$$
改めてオイラーの公式で三角関数で表すと、

今回求めるべき特殊解は、外力の加振が\(sin\)だったので、zの虚部になります。
よって特殊解\(u\)は
$$u=\frac{Xω^2}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}sin(ωt-δ)$$
非同次微分方程式の一般解は、同次方程式の一般解と非同次微分方程式の特殊解の和で表すことができて、
今回の同次方程式の一般解は減衰ありの自由振動の一般解と同じなので、結局求める一般解は下記のようになります。
$$u=e^{-ζωt}Csin(ω_dt+Φ_0)\frac{Xω^2}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}sin(ωt-δ)$$
減衰振動の一般解がわからない人は過去記事を参考にしてください。
振動・波動の基礎②-リアルな振動を考えよう!振動の減衰について詳しく解説
絶対座標系へ戻す
解の形が微妙に違うんだけど…


この解は相対座標系での解だからね。絶対座標系に戻すとちゃんと一致するよ。

ここからは単純に計算をしていくだけなので、スライドを追ってみてください。




このように、絶対座標系で求めた解と一致することが確かめられます。
どちらで計算すべき?

結局どちらで計算すべきかですが、正直、どちらでも構いません。
相対座標だろうが絶対座標だろうが、運動の様子が変わりません。
テストとかで座標系を指定された場合、その座標系で解くのがベターです。
今回計算したように、相対座標系から絶対座標系へ戻すのは結構な手間なので、絶対座標系の解が欲しい場合は、絶対座標系で解く方が楽です。
どちらで解くべきか、しっかりと自分で選択できるようにしておきましょうね。
まとめ

今回は変位加振の運動方程式を相対座標系で解きました。
絶対座標系への変換も行いましたが、なかなかの計算量になりますので、座標系を変換することはあまりお勧めできません。
どちらで解いても運動の状態は変わりませんので、自分が理解しやすい方で解くようにしましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
- 振動・波動:小形正男、裳華房
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎⑤-相平面について-単振動の場合 アニメーションで理解しよう
