振動・波動の基礎④-変位加振・地動加振・調和地動について 強制振動との違いも解説

振動・波動の基礎 変位加振・地動加振 大学物理
物理苦手君
そもそも強制振動の運動方程式のモデルって実際に起こりうるの？
デルタ先生
電気回路とかの分野では強制振動のような現象は発生するよ。

でも構造物が地震などで揺れる場合は少し変わってくるんだ。

これまで、繋がれた質量に直接的に外力を与えて振動させる、強制振動の解説をしてきました。

参考記事

振動・波動の基礎　③強制振動と共振について

今回は、振動の変位加振（地動加振、調和地動とも言います）について解説します。

本記事をおススメする人
  • 強制振動と変位加振（地動加振・調和地動）の違いを知りたい人
  • 物理を勉強していて興味がある人、仕事で振動の知識を使う人

動画でも解説をしていますので、是非参考にしてください。

変位加振（地動加振）とは？

強制振動とのモデルの違い

変位加振は、繋がれた質点に間接的に力を加え、振動させたときの状態を指します。

モデルを見て比較してみましょう。

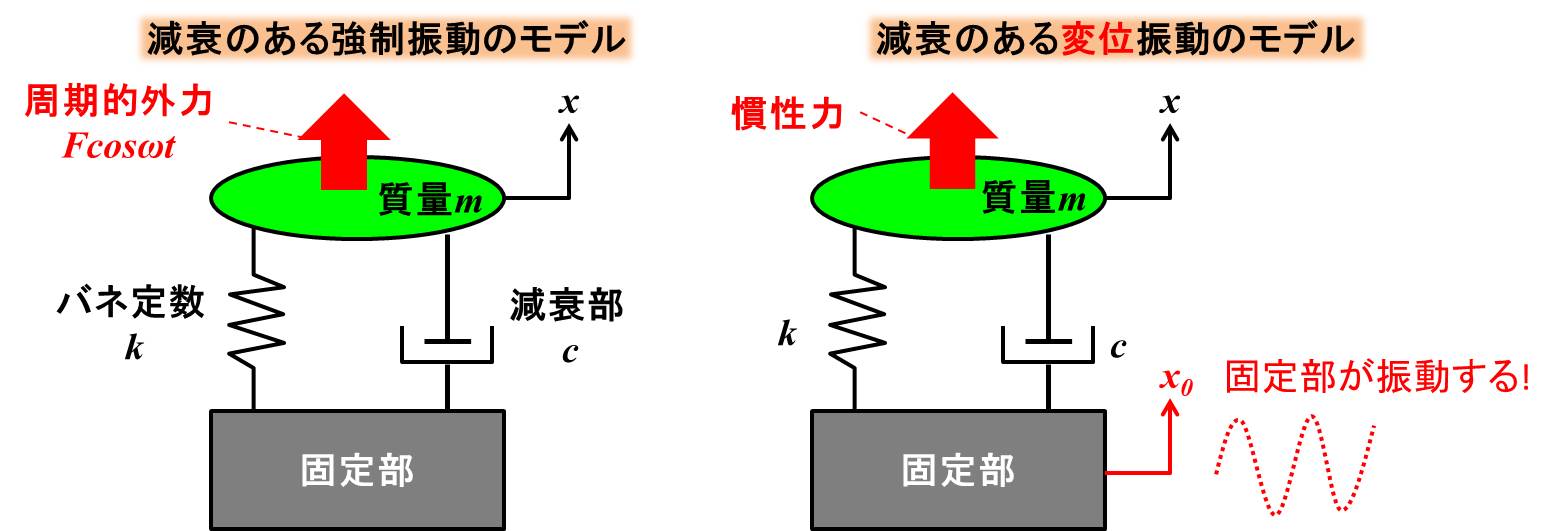
左側がこれまで扱ってきた強制振動のモデル、右側が変位振動のモデルです。

変位振動のモデルは固定部が揺れて、慣性力で質量を動かします。

今回は絶対座標系で運動方程式を立てていきますので、慣性力を用いた相対座標系での解法を知りたい方は下記を参考にしてください。

振動・波動の基礎④-2 変位加振・地動加振・調和地動の相対座標系での運動方程式を解説

このときの固定部の変位を$x_0$としています。

冒頭の地震の例で言うと、固定部が地面で、質量がビルなどの建物に相当しますね。

運動方程式を解く

さて、それでは違いを考えるにあたって、運動方程式を解くことは避けられません。

運動方程式は、

$$m\ddot{x}+c(\dot{x}-\dot{x_0})+k(x-x_0) = 0$$

$ω_0 = \sqrt{\frac{k}{m}}、ζ =\frac{c}{mω_0}$とすると、

$$\ddot{x}+2ζω_0(\dot{x}-\dot{x_0})+ω_0^2(x-x_0) = 0$$

$x_0$の項を右辺に持ってくると、

$$\ddot{x}+2ζω_0\dot{x}+ω_0^2x =2ζω_0\dot{x_0}+ω_0^2x_0$$

固定部の振動を振幅Xとして、$x_0 = Xcosωt$とすると、$\dot{x_0} = -Xωsinωt$より、

$$\ddot{x}+2ζω_0\dot{x}+ω_0^2x =-2ζω_0ωXsinωt+ω_0^2Xcosωt$$

三角関数の合成公式を使って、右辺を整理します。

三角関数の合成公式
$$Csinx+Dcosx = \sqrt{C^2+D^2}sin(x-δ)$$
$$tanδ = \frac{C}{D}$$

これを使うと

$$\ddot{x}+2ζω_0\dot{x}+ω_0^2x =\sqrt{(2ζω_0ω)^2+(ω_0^2)^2}Xsin(ωt-δ)・・・①$$

 

$$tanδ =\frac{-2ζω_0ω}{ω_0^2} = -\frac{2ζω}{ω_0}$$

 

ここまで式変形をして、①と強制振動の運動方程式②と見比べます。

$$\ddot{x}+2ζω_0\dot{x}+ω_0^2x = fcosωt・・・②$$

左辺が同じで、右辺が違うだけですね？

しかも微分方程式の左辺の形が同じで、右辺は三角関数なので、解となる関数の形は同じになります。

ちなみに、変位型振動の場合、位相差がついていますが、位相差は微分の演算に影響しないので、特殊解の形は同じとなります。

ということで、解き方については強制振動の運動方程式と同じになり、非同次方程式を解くことになります。

強制振動の運動方程式を実際に過去記事で解いていますので、結果だけを引用します。

参考記事

強制振動における共振の計算（減衰あり）

こちらも動画での解説がありますので、参考にしてください。

強制振動の運動方程式の一般解は下記です。

$$x=\frac{f}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}sin(ωt-δ)・・・③$$

変位振動も強制振動も同じ三角関数で表すことができるので、振幅の部分に着目します。

①と②式において、右辺の三角関数の係数を比較して、

$$f → \sqrt{(2ζω_0ω)^2+(ω_0^2)^2}X$$

と③の式を置き換えると、変位振動での振幅が求まりますね。

振幅部分をAとすると

$$A=\frac{\sqrt{(2ζω_0ω)^2+(ω_0^2)^2}X}{\sqrt{(ω_0^2-ω^2)^2+(2ζω_0ω)^2}}$$
$$A=\sqrt{\frac{(2ζ\frac{ω}{ω_0})^2+1}{(1-\frac{ω^2}{ω_0^2})^2+(2ζ\frac{ω}{ω_0})^2}}・X$$

このXの係数部分を伝達関数と言い、$T_f$と示します。

伝達関数は、固定部の振動が質量部分にどのくらい伝わるか、を示した関数になり、

$$T_f = \frac{慣性力による振幅}{固定部の振動の振幅} =\frac{A}{X}$$

よって

$$T_f =\sqrt{\frac{(2ζ\frac{ω}{ω_0})^2+1}{(1-\frac{ω^2}{ω_0^2})^2+(2ζ\frac{ω}{ω_0})^2}}$$

$Ω = \frac{ω^2}{ω_0^2}$とすると、

$$A=\sqrt{\frac{4ζ^2Ω+1}{(1-Ω)^2+4ζ^2Ω}}・X$$

この関数のグラフを書くと下記のようになります。

強制振動のときと同じような図になりますが、厳密には異なります。

イメージ的には、$ω_0$の近くで共振するが、減衰の分だけ低周波数側へ共振周波数はシフトします。

強制振動の変位グラフとの比較

物理苦手君
同じような図というか、ほとんど差がないんだったら知らなくてもいいじゃん！
デルタ先生
じゃあ、強制振動のときの変位と、変位振動のときの変位を比べてみよう。

それでは先ほどのグラフを少し表示を変えて、強制振動のときと並べて比較してみましょう。

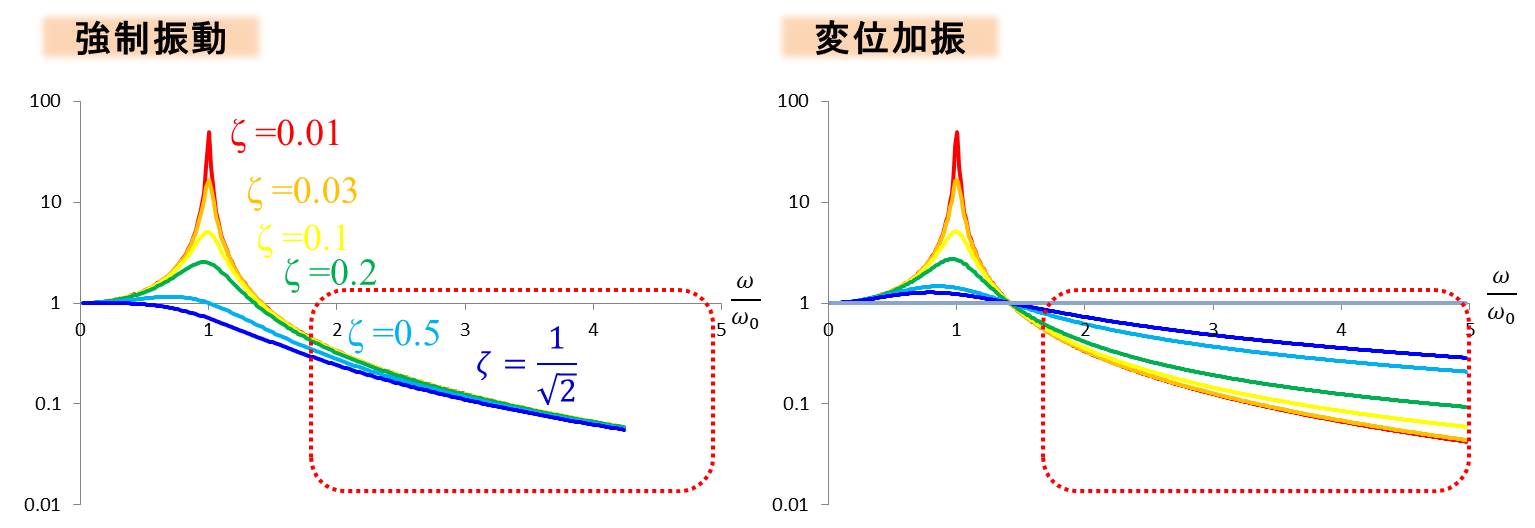
縦軸は振動の応答倍率を対数表示、横軸は$\frac{ω}{ω_0}$で示しています。

応答倍率というのは、与えた力の振幅に対して、質量の振幅が何倍になるかを示しています。

右図のように、変位加振の場合、共振周波数より高い部分で減衰比ζによって値が変動します。

このことから、揺れにくくする構造にするための指針がたちます。

揺れを受けにくくするための例
  1. $ω/ω_0$できるだけ大きくする
  2. 減衰比をζをできるだけ小さくする

減衰比を大きくすればさせるほど、振動はしにくくなります。

その一方で、広い周波数の領域で、加振させた振動の振幅のままになってしまいます。

逆に減衰比を下げると、共振周波数でものすごく共振してしまいます。

ただし共振周波数より高い領域ではほとんど振動しなくなる、という現象が起こるわけです。

そして、共振周波数を高くすると、共振周波数より低い領域では、加振させた振動の振幅で振動してしまいます。

どのような振動を想定するかで、どのような設計にするかは変わってきますが、上記のようなグラフのイメージを持っていれば、設計指針も立てやすくなるでしょう。

まとめ

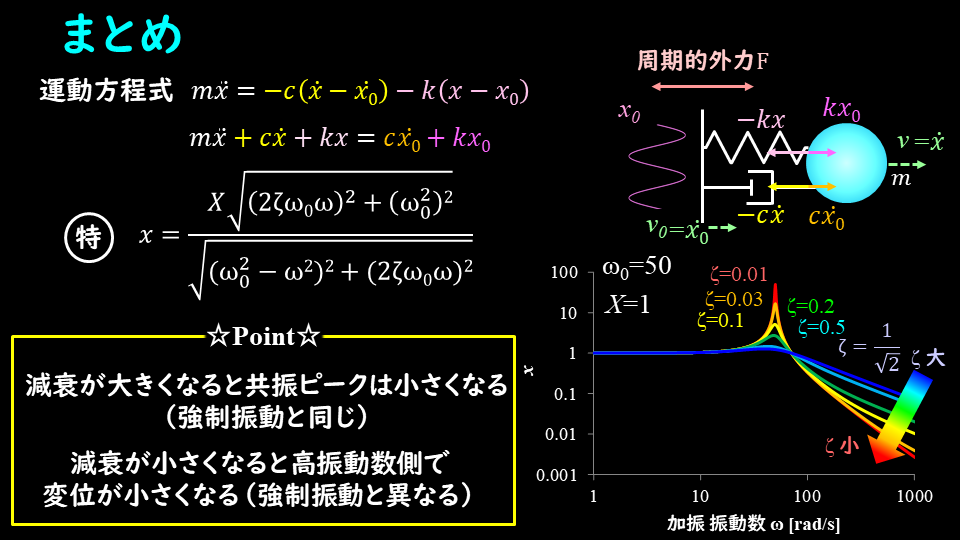
今回は変位加振（地動加振・調和地動）の場合について解説しました。

強制振動のときと大きくは異なりませんが、振動数が高い部分で減衰との関係が少し変わってきます。

この変位加振は、振動の伝達を記述しており、構造設計を行う上で避けては通れないものです。

イメージできるようになれば、応用が利きますので、是非、本記事で理解していただければと思います。

参考文献

  • 振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
  • 機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
  • 構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版
  • 振動・波動：小形正男、裳華房

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

本サイトの振動工学のページはこちら。