運動方程式を解くときにラプラス変換している人がいたんだけど、こんな解き方もあるの?


もちろんラプラス変換を使う解き方もあるよ。ラプラス変換は微分方程式を解くツールの一つだからね。
筆者も論文を読んでてラプラス変換を使って振動の運動方程式を解いているのを見て、驚いた記憶があります。
ラプラス変換自体は、数学的な手法の一つで主に制御工学で使われるのですが、実はもっと幅広い分野で使われています。
そんな便利なラプラス変換、今日は基礎の基礎について解説します。
本記事をおススメする人
- ラプラス変換が全く分からない人
- ラプラス変換のイメージが全くつかない人
- ラプラスでなみのりしたい人
3つ目はふざけました、申し訳ございません。
ラプラス変換ってどういうもの?
ラプラス変換ですが、Wikiを見てみると、非常に難しいことが書いています。
ちょっと初心者には重たい内容なので、わかりやすくざっくり説明すると
- 微分方程式を簡単に解くための数学的な道具
- 積分して時間の関数から別の文字の関数へ変換している
こんな感じです。
簡単な微分方程式であれば、ラプラス変換を使わずとも解くことはできます。
ラプラス変換のイメージ
ラプラス変換のイメージとしては下の図のようになります。
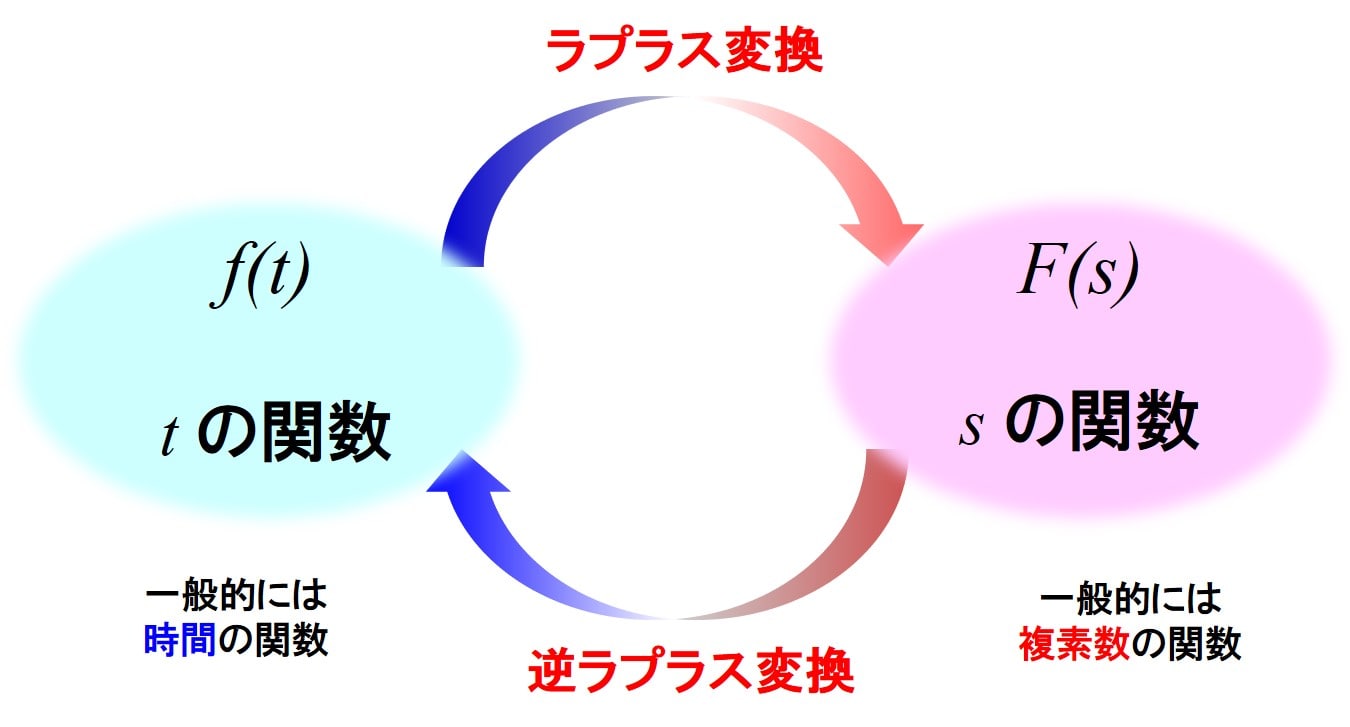
\(t\)の関数\(f(t)\)をラプラス変換すると、別の文字sの関数\(F(s)\)に変換できますよ、
というのがラプラス変換。
一般的に\(f(t)\)は時間の関数、\(F(s)\)は複素数の関数で、
ラプラス変換によって実空間から複素空間へ変換する、というようなイメージでOKです。
ラプラス変換自体はこういう数学的な操作をするものだと思ってください。
そして、ラプラス変換は、微分方程式を解きやすくするもの、と理解ましょう。
ラプラス変換の式
それではラプラス変換の式を見てみましょう。
$$F(s)=\int_0^\infty e^{-st}f(t)dt\tag{1}$$
ただし、変換するには条件があり、右辺の積分の中が収束することが条件です。
基本的には\(e^{-st}\)という指数関数が存在していますので、大体の関数で収束します。
収束しやすいからこの\(e^{-st}\)をかけて積分している、という側面もあります。
例題
\(f(t)=A\)
\(f(t)\)が一定の場合を考えてみましょう。
(1)式に代入して計算してみると
$$\begin{eqnarray}F(s) &=& \int_0^\infty e^{-st}Adt\\&=& A\int_0^\infty e^{-st}dt\\&=&-\frac{A}{s}\left[e^{-st}\right]^\infty_0\\&=&-\frac{A}{s}(0-1)\\&=&\frac{A}{s}\end{eqnarray}\tag{2}$$
定数\(A\)を\(s\)で割ったものが解になりました。
\(f(t)=At\)
では\(f(t)\)が1次関数のときを考えてみましょう。
積分の中にtの1次関数と指数関数の積が入っていますので、部分積分を使って求めていきます。
$$\begin{eqnarray}F(s) &=& \int_0^\infty e^{-st}Atdt\\&=&\left[\frac{-1}{s}e^{-st}・At\right]^\infty_0-\int_0^\infty A\frac{-1}{s}e^{-st}dt\\&=&0+\frac{A}{s}\int^\infty_0e^{-st}dt\\&=&\frac{A}{s}\left[\frac{-1}{s}e^{-st}\right]^\infty_0\\&=&-\frac{A}{s^2}(0-1)\\&=&\frac{A}{s^2}\end{eqnarray}\tag{3}$$
\(f(t)=At^2\)
2次関数のときも部分積分を使います。
\(t\)の次数を落とすために2回の部分積分を行いますが、\(t\)が1次の項は(3)式を求める際に計算していますので、流用しましょう。
$$\begin{eqnarray}F(s) &=& \int_0^\infty e^{-st}At^2dt\\&=&\left[\frac{-1}{s}e^{-st}・At^2\right]^\infty_0-\int_0^\infty 2At\frac{-1}{s}e^{-st}dt\end{eqnarray}\tag{4}$$
第一項は計算すると0になります。
次に積分の部分だけ取り出すと、
$$-\int_0^\infty 2At\frac{-1}{s}e^{-st}dt=\frac{2}{s}\color{red}{\int_0^\infty e^{-st}Atdt}\color{black}{}\tag{5}$$
このようになり、赤字の部分は\(f(t)=At\)のラプラス変換と全く同じになります。
よって(5)式は
$$\frac{2}{s}\color{red}{\int_0^\infty e^{-st}Atdt}\color{black}{}=\frac{2}{s}*\color{red}{\frac{A}{s^2}}\color{black}{}\tag{6}$$
となります。
これがラプラス変換されたときの結果ですので、結局、解は下記のようになります。
$$F(s)=\frac{2A}{s^3}\tag{7}$$
まとめ
ラプラス変換すると、ある程度規則的なものが見えてきたのではないでしょうか?
毎回ラプラス変換をする際に、積分すると大変ですので、結果についてはある程度暗記しておくと早いです。
暗記が苦手な人は、覚えるべきラプラス変換を表にしていますので、表を見ながらラプラス変換しましょう。
なんにせよ、ラプラス変換が何かということを理解しないと、使い方がわからないと思いますので、
次の記事ではもう少し深い部分まで解説します。
