振動・波動の基礎-⑱振動分野でラグランジュの運動方程式を使ってみよう

多自由度の振動を扱う際に、ラグランジュの運動方程式の運動方程式を使うことがありますので、今回は、

なぜラグランジュの運動方程式を使うのか？

振動の分野ではどのような形になるのか？

について詳しく解説します。

具体的な使い方については、また後日、記事にさせていただきますね。

また、ラグランジュの運動方程式を使わずに、運動方程式を立てるやり方についても解説していますので、参考にしてください。

ラグランジュの運動方程式とは

オイラー＝ラグランジュの運動方程式とも呼ばれます。

ラグランジュの運動方程式の特徴は、ざっくりと下記の2つがあります。

これら二つに共通しているのは、計算が楽になる、ということであり、これが多自由度の振動の計算でラグランジュの運動方程式が使われる理由です。

ラグランジュの運動方程式の形

外力や非保存力が作用していない場合のラグランジュの運動方程式は下記のようになります。

$$\frac{d}{dt}(\frac{\partial L}{\partial\dot{q}_i})-\frac{\partial L}{\partial q_i}=0\tag{1}$$

ここでLはラグラジアンで運動エネルギーと位置エネルギーの差分になります。

また、一般化座標とよばれる座標系\(q_i\)を使います。

ここでは、まずこういう定義になっている、と思っておいてください。

ラグランジュの運動方程式の立て方

やり方としては、

下記のような一番簡単な、バネにつながれた質点を考えてみましょう。

バネ定数を\(k\)、質量を\(m\)、変位量を\(x\)として、右側を正の向きに取ります。

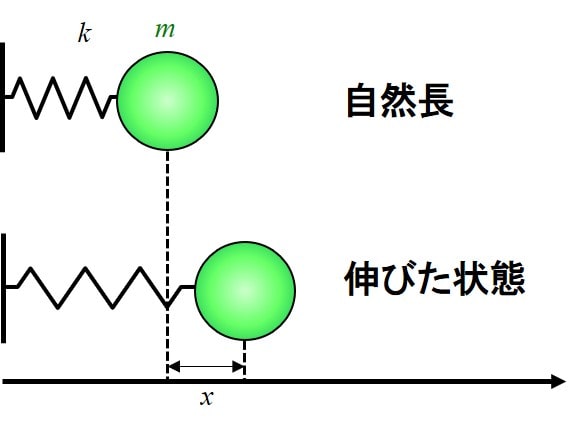
エネルギーのことを考えなくても、運動方程式は古典力学では、下記のようになりますね。

$$m\ddot{x}+kx=0\tag{2}$$

これをエネルギーの観点で見てみましょう。

質点の運動エネルギーを\(T\)、ポテンシャルを\(U\)とすると、

$$T=\frac{1}{2}m\dot{x}^2\tag{3}$$

$$U=\frac{1}{2}kx^2\tag{4}$$

ポテンシャルUはバネの弾性エネルギーとなりますね。

これを用いてラグランジュの運動方程式に代入するのですが、ラグラジアンLを計算しておきましょう。

ラグラジアン\(L\)は運動エネルギー\(T\)とポテンシャル\(U\)の差分なので、下記のようになります。

$$L=T-U=\frac{1}{2}m\dot{x}^2-\frac{1}{2}kx^2\tag{5}$$

このラグランジアンを(1)式のラグランジュの運動方程式に入れて計算してみましょう。

(1)のラグランジュの運動方程式は一般化座標\(q_i\)を用いていますので、\(x\)を用いて書き直すと、

$$\frac{d}{dt}(\frac{\partial L}{\partial\dot{x}})-\frac{\partial L}{\partial x}=0\tag{6}$$

つまりは、一般化座標に\(xyz\)などの座標系も入れて大丈夫、ということです。

ちなみに極座標などの座標系でも大丈夫で、ラグランジュの運動方程式は座標系が異なっても成立します。

それでは第1項ですが、速度の偏微分がありますので、運動エネルギーについて微分すればよくて、

$$\frac{d}{dt}(\frac{\partial L}{\partial\dot{x}})=\frac{d}{dt}(\frac{\partial T}{\partial\dot{x}})=m\ddot{x}\tag{7}$$

続いて第2項は、変位量の偏微分がありますので、こちらはポテンシャルについて微分すればよく、

$$\frac{\partial L}{\partial x}=-\frac{\partial U}{\partial x}=-kx\tag{8}$$

ラグランジュの運動方程式は(7)-(8)=0だから、

$$m\ddot{x}+kx=0$$

となり、いつも通りの運動方程式が求まりました。

強制振動の場合と減衰がある場合

これまでは、減衰のない自由振動という一番簡単な例で考えていました。

しかし振動の世界には外力がある強制振動であったり、減衰が存在する減衰振動などがあります。

これらに対応できるように、一般化力\(Q_i\)とエネルギーの散逸関数\(F\)を定義します。

ここで\(i\)は自由度を示していて、\(i=1,2,3・・・N\)とします。

一般化力は一般化座標の中での非保存力（強制振動では外力の成分に相当）であり、散逸関数は減衰に相当するもの、と考えてください。

一般化力を\(Q_i\)とし、散逸関数\(F\)を下記のように定義します。

$$F=\frac{1}{2}\sum_{i=1}^N\sum_{k=1}^Nc_{ik}\dot{q}_iq_k\tag{9}$$

これらを用いて、ラグランジュの運動方程式を拡張すると、

$$\frac{d}{dt}(\frac{\partial L}{\partial\dot{q}_i})-\frac{\partial L}{\partial q_i}+\frac{\partial F}{\partial \dot{q}_i}=Q_i\tag{10}$$

このような形になります。

ラグランジュの運動方程式を使うメリット

このラグランジュの運動方程式を使うメリットですが、冒頭で説明した通り、

という点から、計算が楽になる、ということでした。

でも、今回のような単純な１自由度の振動などを扱うと、かえって難しくなることもあります。

では、どういうときに使えばよいのかというと、ラグランジュの運動方程式が力を発揮するのは、N自由度とか自由度が増えたときになります。

また、\(xyz\)座標系（デカルト座標）では向きを考えて正負の符号をつけないといけない場面がありますが、ラグランジュの運動方程式を使うと、

機械的に(10)式に当てはめていけば、勝手に運動方程式が出てくる、という点がメリットになります。

ラグランジュの運動方程式は解析力学などで習うことが多いと思いますが、

運動方程式を解くためのツールの一つにすぎませんので、その問題にあった解法を考えて使うかどうか判断しましょうね。

まとめ

ラグランジュの運動方程式について解説しました。

ラグランジュの運動方程式は、エネルギーの観点から立てた運動方程式で、向きを考慮しなくてもよいので、計算が楽になる（ことがある）というものでした。

ラグランジュの運動方程式は下記のような形です。

$$\frac{d}{dt}(\frac{\partial L}{\partial\dot{q}_i})-\frac{\partial L}{\partial q_i}+\frac{\partial F}{\partial \dot{q}_i}=Q_i\tag{10}$$

\(q_i\)は一般化座標で、\(xyz\)座標であれば\(x\)や\(y\)、\(z\)を代入すればOKです。

\(L\)はラグラジアンで、運動エネルギーを\(T\)、ポテンシャルを\(U\)として、

$$L=T-U$$

\(F\)は散逸関数で減衰を示していて、

$$F=\frac{1}{2}\sum_{i=1}^N\sum_{k=1}^Nc_{ik}\dot{q}_iq_k\tag{9}$$

\(Q_i\)は一般化力で、強制振動における外力を示しています。

あとは問題で与えられた条件を代入して、機械的に微分していけば運動方程式が求まります。

以上が振動分野で扱うラグランジュの運動方程式ですが、このラグランジュの運動方程式は、ほかの分野でもよく使われますので、理解しておくと応用が利きます。

参考文献

• 振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
• 機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

本サイトの振動工学のページはこちら。

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎-⑲2自由度の振動にラグランジュの運動方程式を使ってみる！