1自由度の振動にラグランジュの運動方程式を使えるのはわかったんだけど、多自由度でも使えるの?


使えるよ、今日は2自由度での振動に使ってみよう。
今回は2自由度の振動の運動方程式をたてる際に、ラグランジュの運動方程式を使って解きます。
運動方程式を立てるやり方は1自由度のときと全く同じですので、計算過程をしっかり見ていきましょう。
本記事をおススメする人
- ラグランジュの運動方程式を使って2自由度の振動の運動方程式を解きたい人
- ラグランジュの運動方程式が大好きな人
- 2自由度の運動方程式を何とかして解きたい人
2自由度の振動のモデル
まずは扱うモデルについて下に示します。
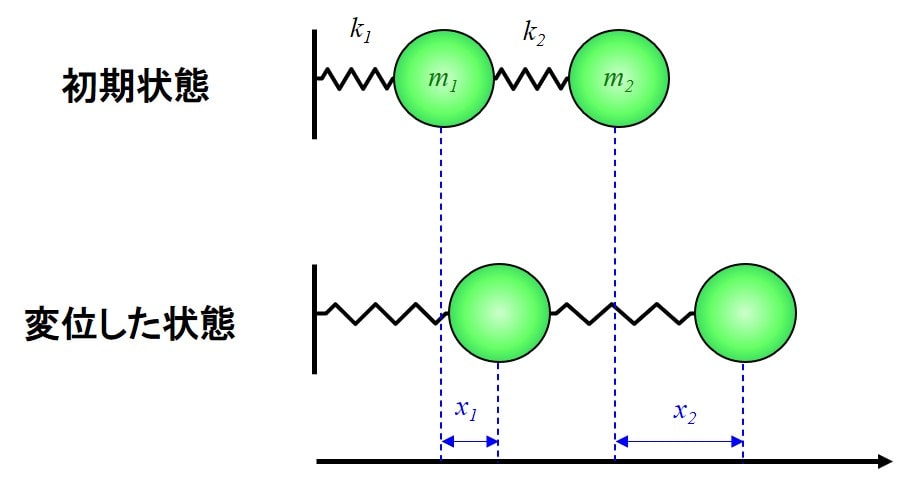
今回は、2つの質点がバネにつながれていて、片側だけ固定されているような場合を考えます。
ラグランジュの運動方程式の復習
ラグランジュの運動方程式は過去の記事で解説していますので、詳細は過去記事をご確認ください。
大事なポイントは、ラグランジュの運動方程式はエネルギーの観点から立てるのでした。
立て方としては、3ステップです。
ポイント
- ラグラジアンを求めるために、運動エネルギーとポテンシャルを計算する
- 減衰や外力などの非保存力を計算する
- ラグランジュの運動方程式に代入する
2自由度の振動の運動方程式を立てる
2つ質点がありますので、運動方程式を立てる必要があります。
運動方程式を立てる
①ラグラジアンLを求める
運動エネルギーを\(T\)、ポテンシャルを\(U\)とすると
$$T=\frac{1}{2}m_1\dot{x}^2_1+\frac{1}{2}m_2\dot{x}_2^2\tag{1}$$
$$U=\frac{1}{2}k_1x_1^2+\frac{1}{2}k_2(x_2-x_1)^2\tag{2}$$
ラグラジアン\(L\)は\(L=T-U\)なので、(1)-(2)より、
$$L=T-U=\frac{1}{2}m_1\dot{x}^2_1+\frac{1}{2}m_2\dot{x}_2^2-\frac{1}{2}k_1x_1^2+\frac{1}{2}k_2(x_2-x_1)^2\tag{3}$$
非保存力を計算する
今回は減衰部分(ダンパー)や外力が無い系ですので、ここは飛ばします。
ラグランジュの運動方程式に代入する
ラグランジュの運動方程式は下記です。
$$\frac{d}{dt}(\frac{\partial L}{\partial\dot{q}_i})-\frac{\partial L}{\partial q_i}=0\tag{4}$$
\(q_i\)となっている部分が座標(正確には一般化座標)を示しているので、\(q_i=x_1 or x_2\)として、計算します。
1自由度の計算をした過去記事でも同じことをしていますので、そちらも参考にしてください。
では、\(q_i=x_1\)のとき、(4)式の第一項を計算してみましょう。
第一項は、速度の偏微分がありますので、運動エネルギーに対して微分すればよくて、
$$\frac{d}{dt}(\frac{\partial L}{\partial\dot{q}_i})=\frac{d}{dt}(\frac{\partial T}{\partial\dot{x}_1})=m_1\ddot{x}_1\tag{5}$$
次に第二項は、変位量の偏微分がありますので、こちらはポテンシャルについて微分して、
$$\frac{\partial L}{\partial q_i}=-\frac{\partial U}{\partial x_1}\\=-k_1x_1-k_2x_1+k_2x_2\tag{6}$$
ラグランジュの運動方程式は(5)-(6)ですので、
$$m_1\ddot{x}_1+k_1x_1+k_2x_1-k_2x_2=0\tag{7}$$
これが左側の質点\(m_1\)に関する運動方程式です。
次に右側の質点\(m_2\)に関する運動方程式を求めます。
ラグランジュの運動方程式に代入する際に\(q_i=x_2\)として、計算すれば、右側の質点に関する運動方程式が求まります。
第一項は、速度の偏微分がありますので、運動エネルギーに対して微分すればよくて、
$$\frac{d}{dt}(\frac{\partial L}{\partial\dot{q}_i})=\frac{d}{dt}(\frac{\partial T}{\partial\dot{x}_2})=m_2\ddot{x}_2\tag{8}$$
次に第二項は、変位量の偏微分がありますので、こちらはポテンシャルについて微分して、
$$\frac{\partial L}{\partial q_i}=-\frac{\partial U}{\partial x_2}=k_2x_1-k_2x_2\tag{9}$$
ラグランジュの運動方程式は(8)-(9)ですので、
$$m_2\ddot{x}_2-k_2x_1+k_2x_2=0\tag{10}$$
このように右側の運動方程式もラグランジュの運動方程式を使って求めることができます。
まとめ
今回は2自由度の振動について、ラグランジュの運動方程式から、運動方程式を求めました。
運動方程式の作り方もいくつか数学的な手法があり、その一つがラグランジュの運動方程式です。
テストに出る!とかでなければ、自分に合ったやり方で運動方程式を立て、その意味を考えられることが重要ですので、
このラグランジュの運動方程式のやり方が自分に合っている、というのであれば突き詰めていけばよいと思います。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら