高校物理-力学 力の分解もベクトルで！アニメーションで学ぼう

高校1年生の方は最初の難関じゃないでしょうか？

習ったことのないベクトルと三角関数が出てきて、『なんじゃこりゃ？？』ってなっちゃうところです。

（筆者もそうでした・・・）

本記事ではこんな人におススメです。

力の分解

ベクトルの分解

力の分解です。

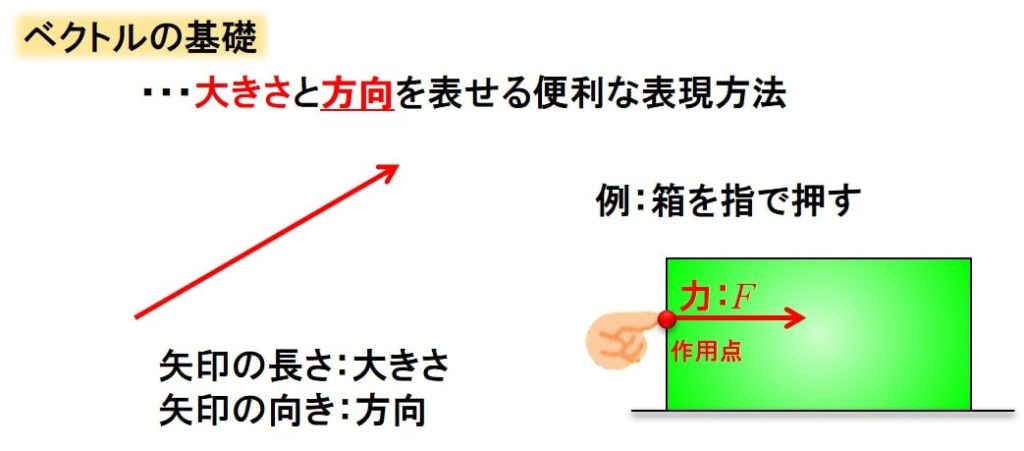
今まで力を矢印で書いてきましたが、これは数学でベクトルと呼んでいるものです。

ベクトルには、１とか２とか、ベクトル自体の大きさと、向きを表すことができます。

力のベクトルの場合、 作用点を出発点として、 力が発生している向きに矢印を書きます。

ベクトルの大事な考え方として、いろんな方向に分解したり、足し合わせたりできます。

今回は力の分解について、アニメーションで見てみましょう。

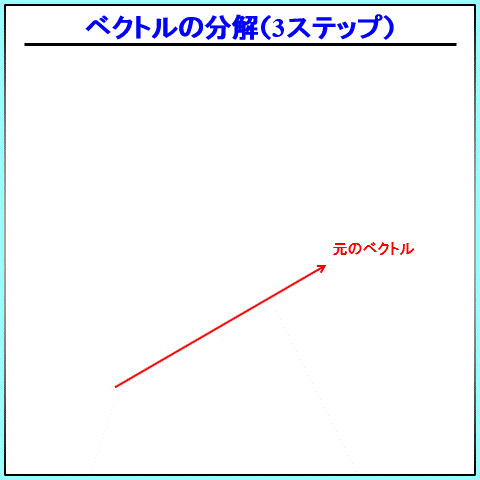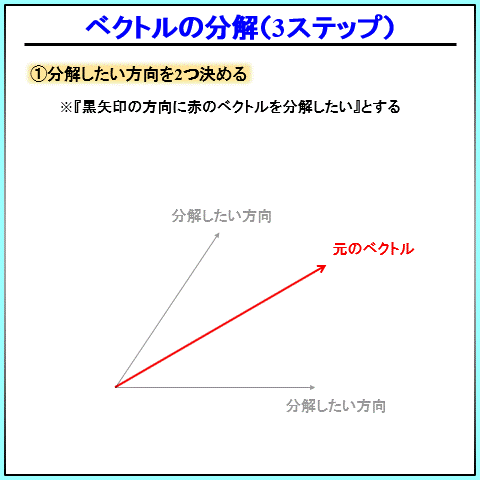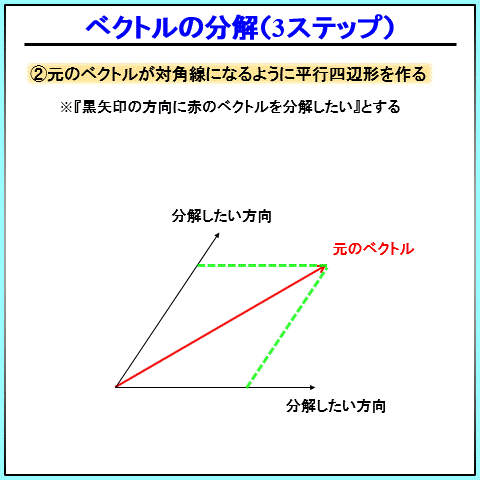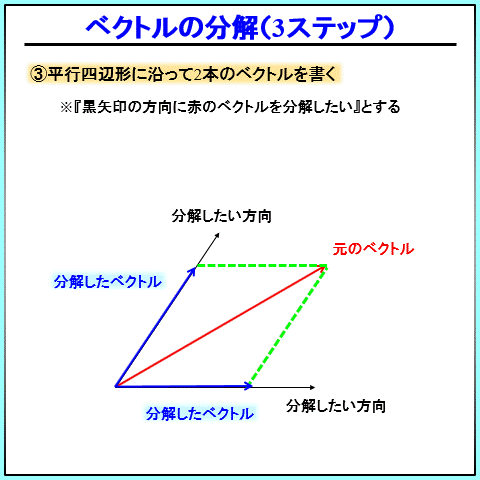
こんな感じの3ステップです。

ちなみに、平行四辺形で分解すると、あとの三角関数の計算がややこしくなることが多いので、力学では基本的に長方形を書いて分解します。

こういう形です。

直角三角形が見えてくると思いますが、直角三角形だと、三平方の定理を使えたり、三角関数の計算が楽になったりするので、計算がしやすいメリットがあります。

三角関数・・・と聞いてゾッとした方もいらっしゃるかもしれませんが、次に解説しますね。

分解した力の表し方：三角関数

そして分解した力の表し方です。

これには三角関数を使います。

三角関数の表し方ですが、直角三角形を書いたときに、下記のようになります。

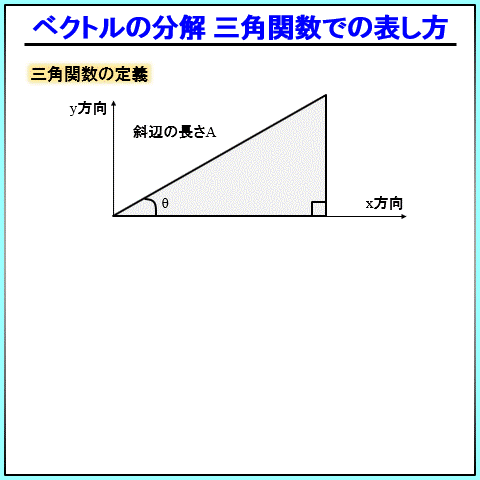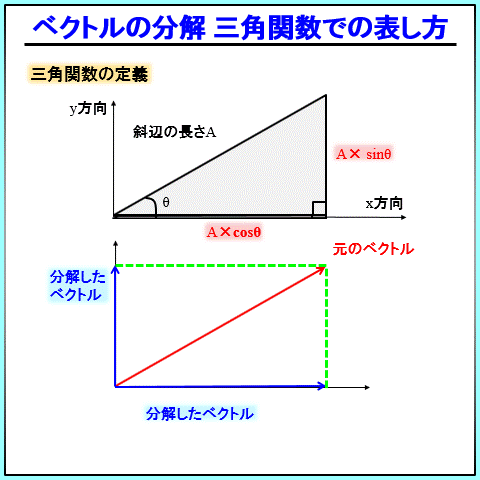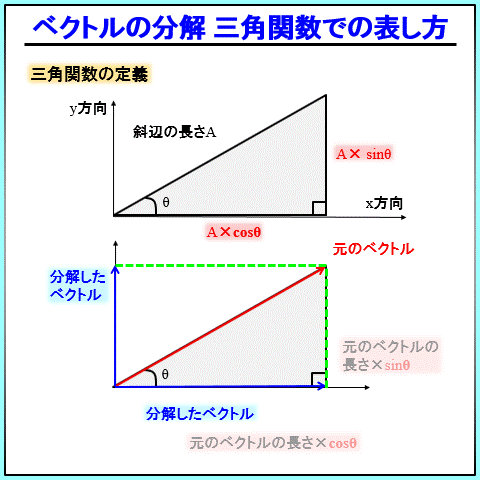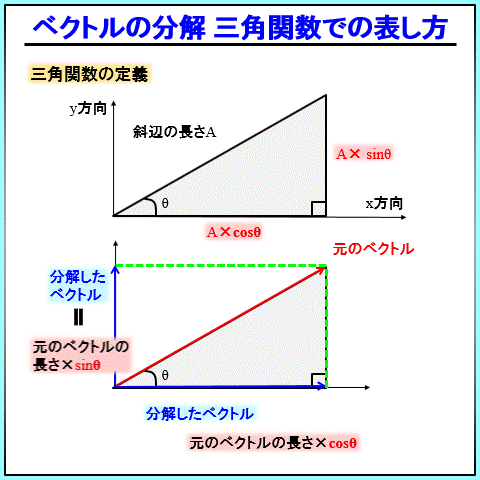
斜辺の長さを\(A\)、角度を\(θ\)とすると、\(x\)が\(Acosθ\)、\(y\)が\(Asinθ\)です。

まずはこれだけ覚えてください。\(x\)が\(cosθ\)、\(y\)が\(sinθ\)・・・\(x\)が\(cosθ\)、\(y\)が\(sinθ\)・・・

呪文のように唱えてください。

これに斜辺の長さをかけるだけです。

これは数学でも超重要で、よく使いますのでよく覚えておきましょう。

それではよくある例を見て、考え方に慣れていきましょう。

例：斜面のボール（摩擦無しで滑っている状態）

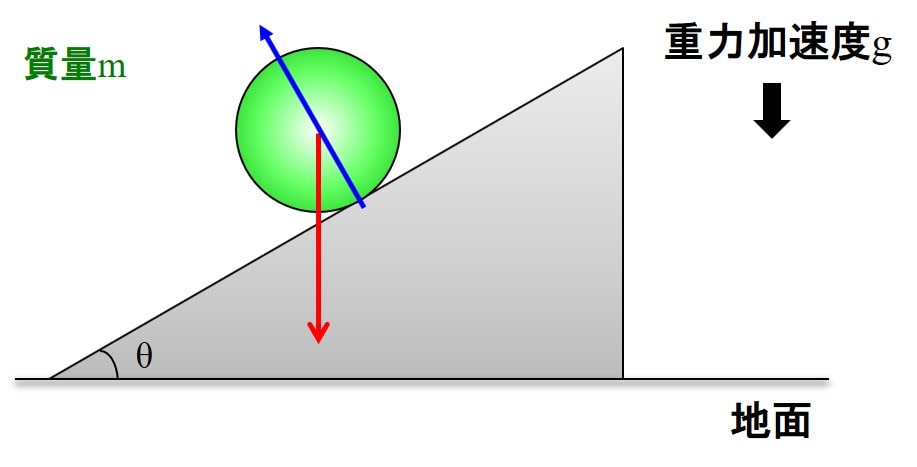
まず、摩擦無しで重力だけ働いている場合を考えましょう。

ボールは加速度\(a\)で滑っています。

ボールの質量を\(m\)、重力加速度を\(g\)とすると、重力は、真下の方向に発生します。

考え方としては、

という流れです。

働いている力は重力なので、この重力を 加速度運動している方向と、その垂直な方向に分解します。

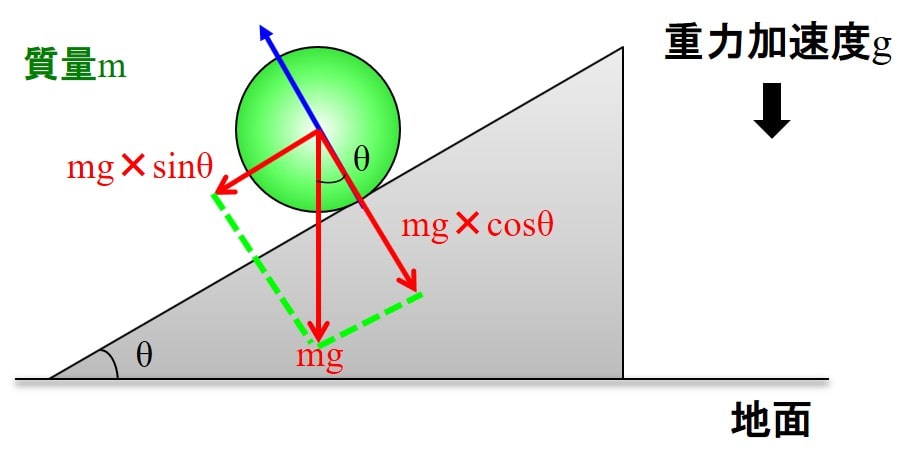
加速度運動している方向の力\(F\)は、斜面の角度を\(θ\)とすると、

$$F=mg × sinθ$$

となりますね。

ちなみに、斜面と垂直な方向には力がつりあっています。

イメージがつかない人は、斜面を水平にして見てみましょう。

こんな感じ。斜面を水平にするために回転させてます。

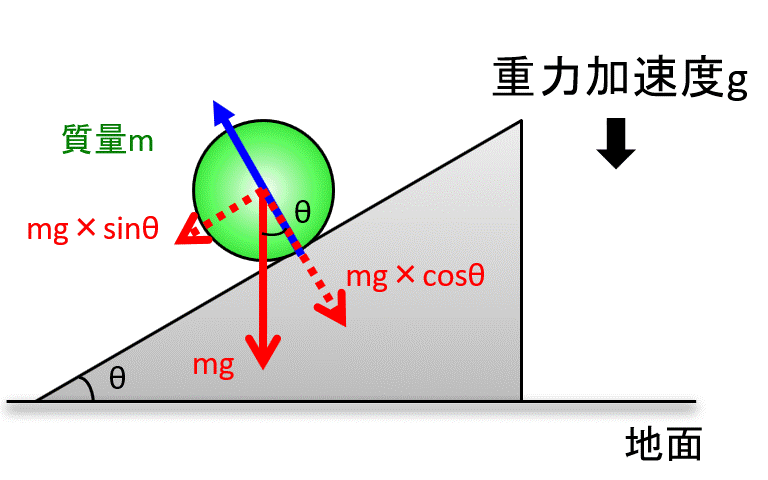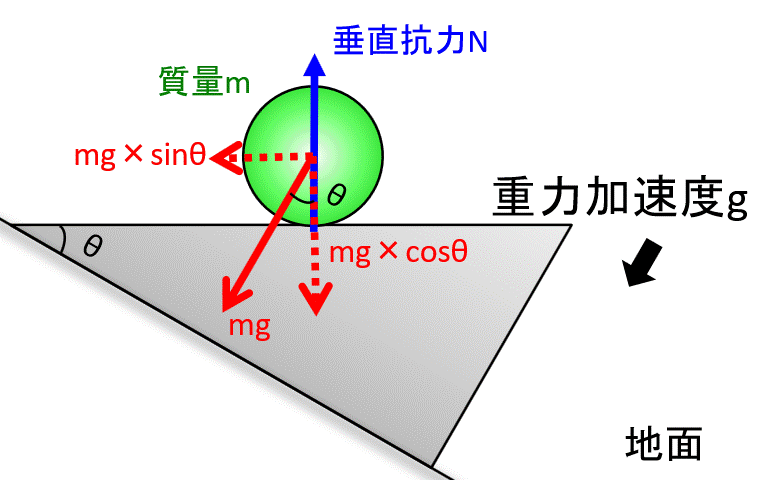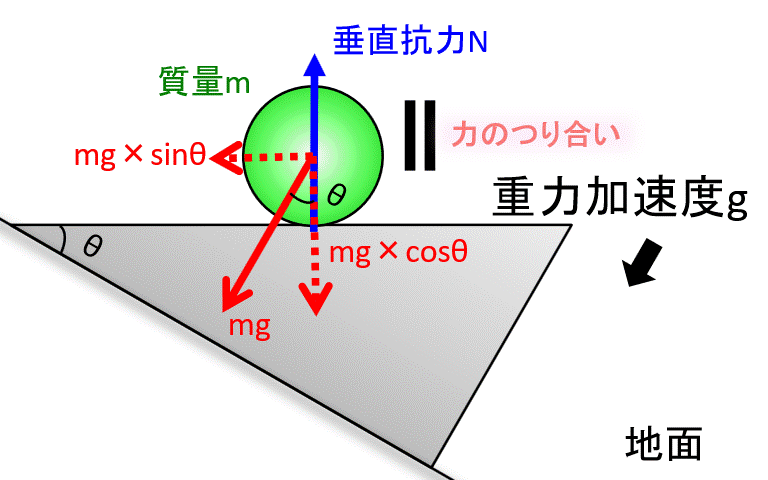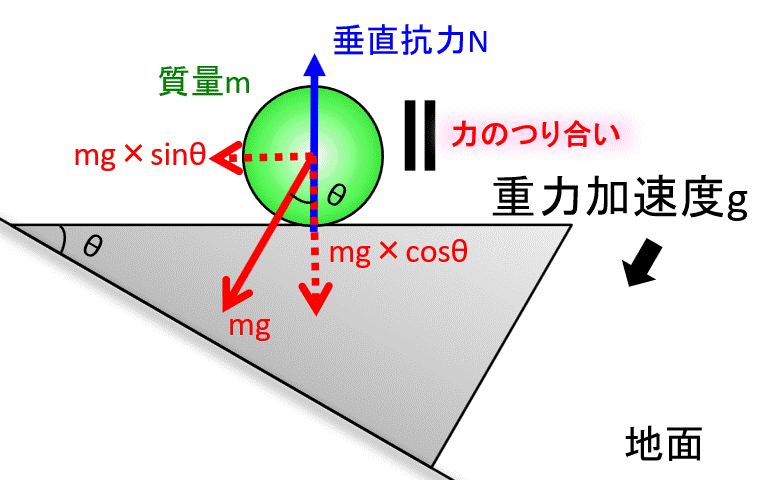
斜面と垂直な方向でつりあっていないと、ボールは斜面にめり込むか、飛んで行ってしまいますね。

垂直抗力を\(N\)とすると、斜面に垂直な力がつりあっているので、力のつり合いから、

$$N=mg cosθ$$

以上で、この問題における力がすべて明らかになりましたね。

まとめ

以上、力の分解と分解したベクトルを三角関数で表すことを解説しました。

力の分解の3ステップは下記です。

分解する際は、 平行四辺形より、長方形を作る方が計算しやすくなります。

また、力を分解する方向の考え方は下記です。

1つ方向を決めたら、長方形を作るために、決めた方向に垂直な方向に力を分解するようにしましょう。

この基本さえ理解しておけば、基礎的な問題は解けるようになりますので、しっかり理解しましょう。

このブログを読み終えた状態というのは、『武器をもらって、取り扱い説明書を読んだ状態』です。

武器を使いこなすには、問題を解いて、しっかりと実戦で使いこなせるようにしましょう。

力の分解ができたら次は力の合成です。下の記事を参考にしてくださいね。

高校物理の力学　力の合成についてアニメーションで学ぼう