多自由度の振動の自由振動はわかったんだけど、今までとやってきたことと同じだね、これって勉強する意味あるの?


一般解を求めるだけだとおもしろくないよね。多自由度系を扱うメリットは固有振動モードがわかる、というところにあるから、そこまで理解していこう。
今回から多自由度系で一番大事な部分、固有振動モードについて解説します。
少し長くなりますので、今回は自由振動の解を示すところまで示します。
ここが多自由度の振動を学ぶメリットの部分になりますので、しっかりと理解しておきましょう。
計算がわからなくても、多自由度系を扱うことで固有振動モードが計算できる、という事実を抑えておきましょう。
参考記事
本記事をおススメする人
- 多自由度の振動を勉強している人
- 固有振動モードの計算をしたい人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
下記の動画でも解説していますので、参考にしていただければと思います。
減衰なしの運動方程式
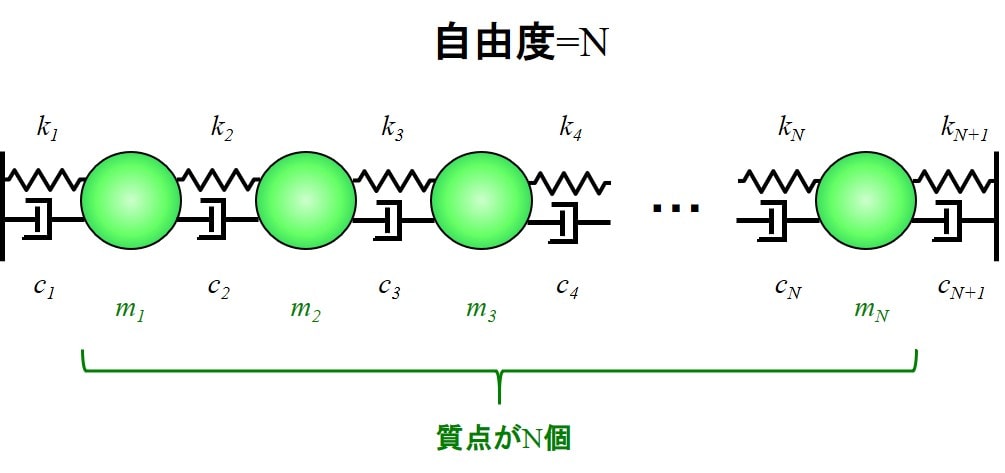
N自由度の多自由度系のモデルを上の図で示しています。
このモデルは減衰ありですね。
運動方程式については、過去の記事で運動方程式まで立てていますので、詳細はそちらを参考にしてください。
結果だけ引用しますと、運動方程式は、
$$M\ddot{X}+C\dot{X}+KX=0\tag{1}$$
\(M\)、\(C\)、\(K\)はそれぞれ質量マトリックス、減衰マトリックス、弾性マトリックスで、\(X\)は位置のベクトルです。
今回は減衰無しで考えますので下記のようなモデルになります。
-min.jpg)
\(i=1,2,3,・・・,N\)として、
\(m_i\):\(i\)番目の質点の質量
\(k_i\):\(i\)番目のバネのバネ定数
\(x_i\):\(i\)番目の質点の位置
運動方程式は(1)式の減衰マトリックスをゼロにして、
$$M\ddot{X}+KX=0\tag{2}$$
となります。
一般解を求める
N自由度の振動の一般解ですが、大事なポイントを先に示しておきますと、
N自由度の振動の一般解は、 それぞれの固有振動の和で表されます。
実際に運動方程式を解いて、この事実を見てみましょう。
運動方程式を解く
(2)式は単振動の運動方程式が行列になっているような形ですね?
行列になっているだけで、中身はN個の二階微分方程式なので、特殊解を仮定して、足し合わせれば一般解が求まります。
単振動とよく似た形になっているのであれば、特殊解も三角関数で表せるので、
$$x_i=u_isin(ωt+φ) i=1,2,3…N\tag{3}$$
となります。
(3)式の2回微分を求めておくと、
$$\ddot{x_i}=-ω^2u_isin(ωt+φ) i=1,2,3…N\tag{4}$$
(2)式に(3)、(4)を代入して整理すると、
$$(K-ω^2M)\{u\}=0\tag{5}$$
$$\{u\}=\left(\begin{array}{c}u_1\\u_2\\\vdots\\u_N\end{array}\right)$$
ここで(5)式が\(u_i=0\)以外に解をもつための条件は、
$$det\left[k-ω^2M\right]=0$$
という行列式がゼロにならなければならないので、実際に行列式を書くと、
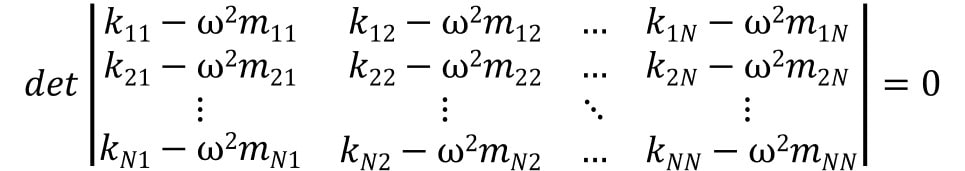
このような式となり、\(ω^2\)のN次方程式を得ます。
これを特性方程式と言ったり、振動数方程式と言ったりします。
このN次方程式の解を\(ω_r\) \((r=1,2,3…N)\)としたとき、\(ω\)を\(r\)次の固有振動数と呼びます。
これらは2自由度の振動のときにも同じことをしているので、参考にしてください。
\(r\)次の固有振動を考えて、\(ω=ω_r\)を(5)式に代入すると、
$$(K-ω^2_rM)\{u_r\}=0\tag{6}$$
ここで、r次の固有振動の振幅を
としています。
(6)式をまじめに書くと
$$\vdots$$
このN個の方程式を解けばよいのですが、行列式がゼロの同次方程式と呼ばれるものになっているので、
振幅\(u_i^r\)の絶対値は求まらないのですが、振幅の比は決まります。
適当に特殊解として\(x_i=u_isin(ωt-φ)\)と解を決めたとき、\(i=1~N\)番目までの解に同じ定数をかけても解として成立する、ということになります。
\(r\)次における定数を\(C_r\)とすると、
$$\{x^r\}=Cr\{u^r\}sin(ω_rt+φ_r)$$
これはベクトルになっていて、\(r\)次の固有振動における\(1~N\)番目の変位を表しています。
自由振動の解は\(1~N\)次の固有振動の和をとればよいので、
これが\(N\)自由度の自由振動の解となります。
大事なこととして、 自由振動はそれぞれの固有振動の和になっている、という点を覚えておきましょう。
まとめ
N自由度の振動について運動方程式を解くことで、自由振動はそれぞれの固有振動の和になっている、ということを示しました。
解き方自体は行列表記に慣れている方は簡単かもしれませんが、行列に慣れていない人は、次回からも行列をたくさん扱っていきますので、しっかり慣れていきましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 →振動・波動の基礎-㉑固有振動モードを導出する!モード座標系を取り入れる!