バネの力って向きがよくわかんないんだよね・・・


じゃあ今日はバネの力について詳細を解説するね。
物理を始めた皆さん、バネの力の向きを間違えたことはありませんか?
本日はバネの力(弾性力)について、解説します。
この記事を読めば、バネの基本について学べます。
結論として、バネの基本的なポイントは
バネの問題のポイント
- 『バネの力は両端に発生する』
- 『バネの力の大きさはフックの法則、向きは図を見て判断』です。
本記事をおススメする人
- 力学を学び始めた方で、バネの力がよくわかっていない人
- バネの力の向きがよくわからない人
- 授業の予習でどんな感じかをつかみたい人
バネの力(弾性力)とフックの法則
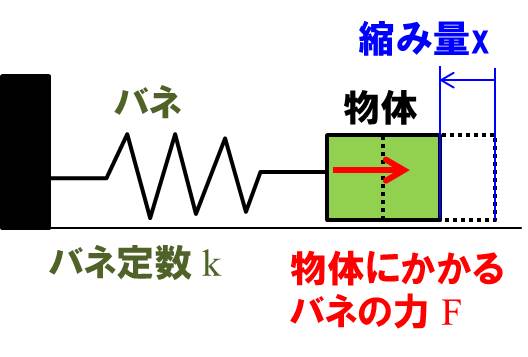
※図はよくあるイメージ図です。
$$F=kx$$
\(k\)はバネ定数、\(x\)は自然長からの変位量です。
バネの力は弾性力とも言います。
有名なフックの法則でバネの力は表されます。
さて、本記事の主張に入ります。
参考書や教科書では\(F=-kx\)と書かれている場合がありますが、これはおススメしません!
プラスかマイナスかは \(F\)がどこの力を示しているかで決まりますので、向きは後で考えます。
バネの力の具体例
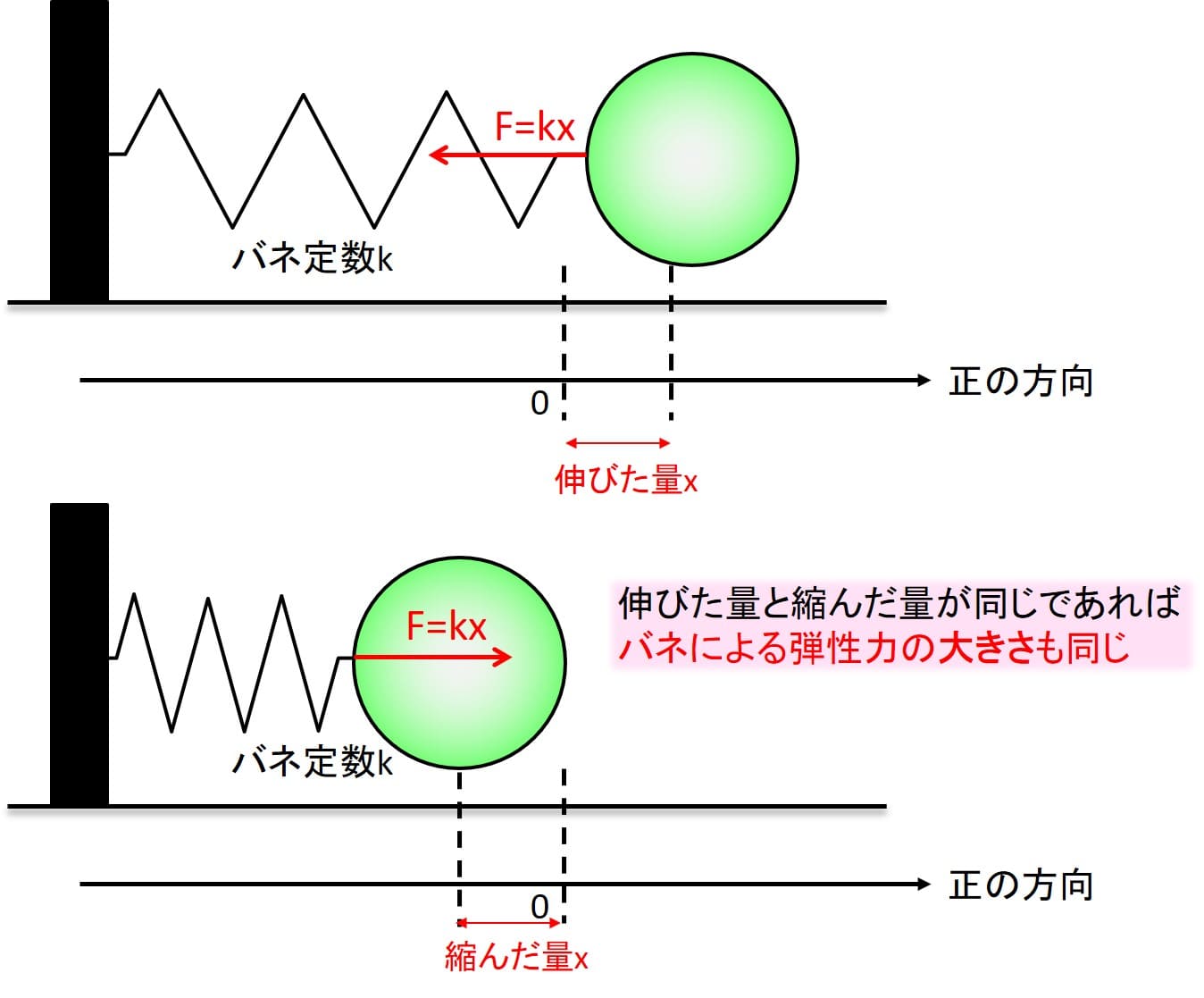
ではよくある下のような図の例を考えましょう。
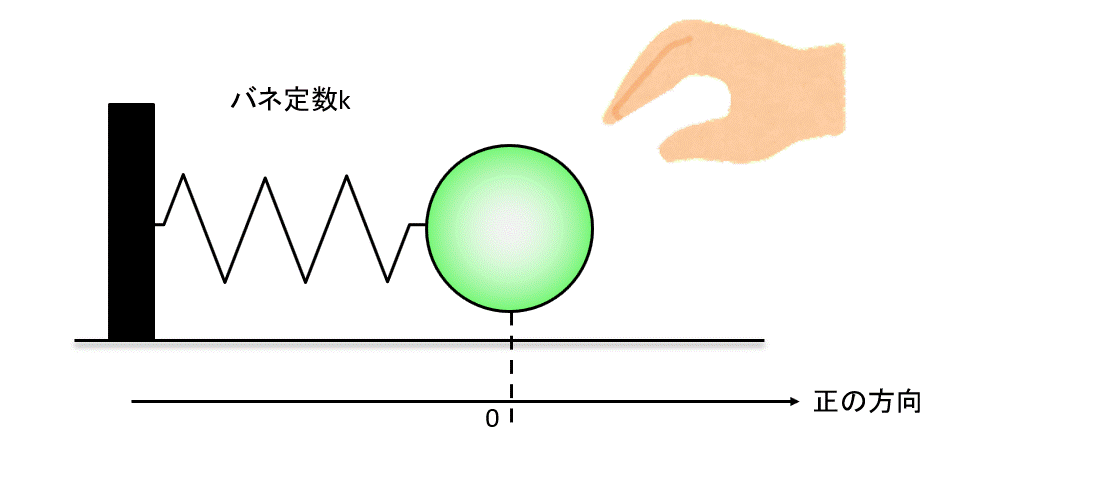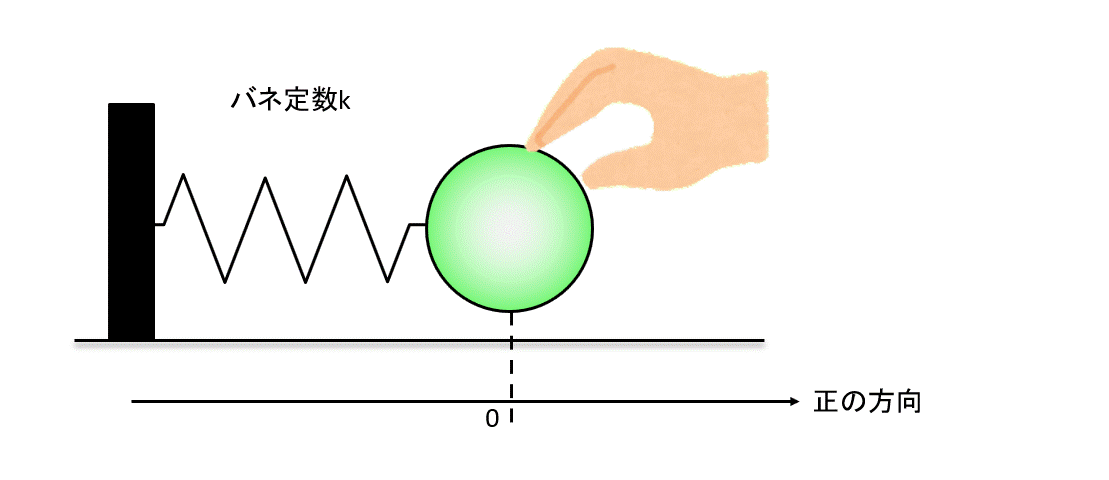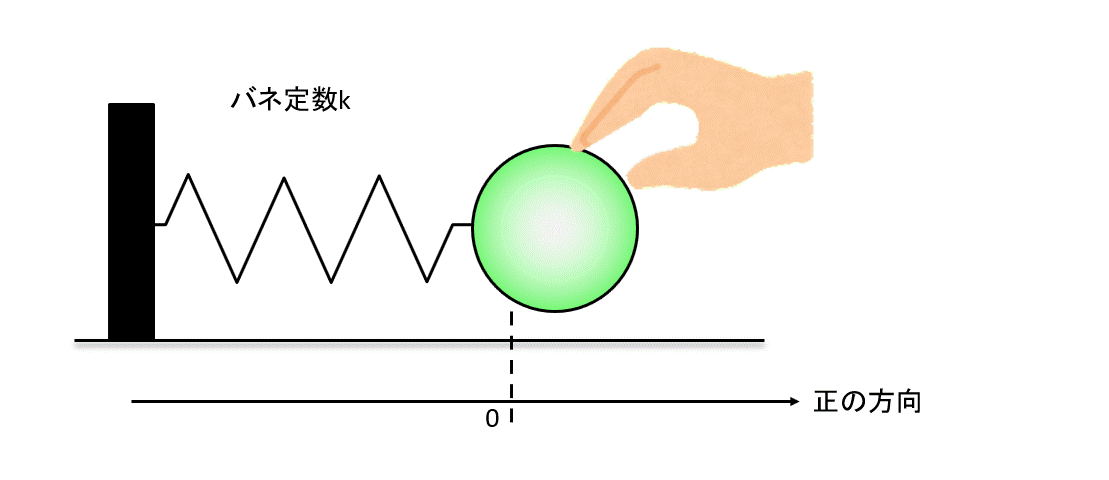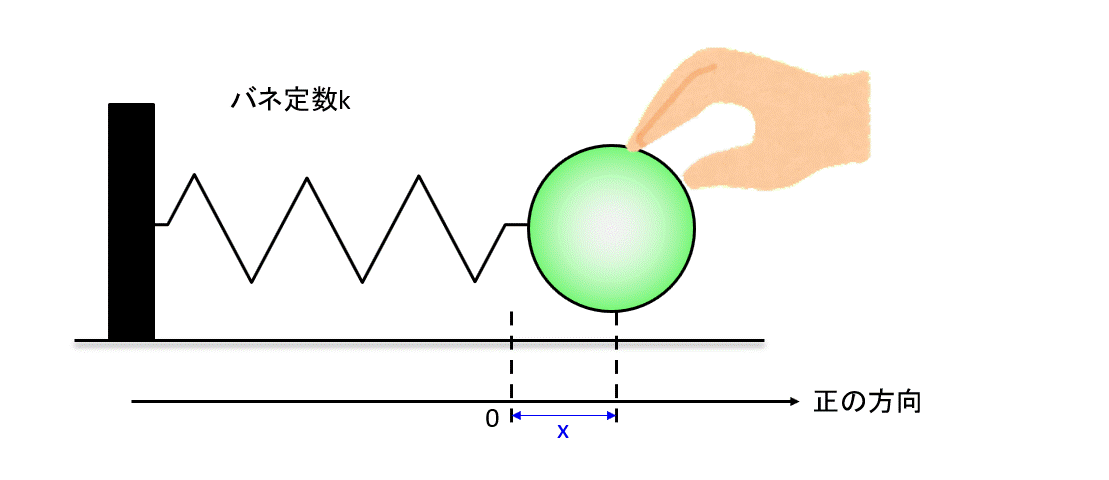
壁にバネでつながれているボールを引っ張ります。
引っ張る方向を正の方向、プラスにとります。
さて、ボールを引っ張り、バネを\(x\)だけ伸ばしたときに発生する力を考えましょう。
\(x\)が大きくなるとフックの法則で発生する力は大きくなります。
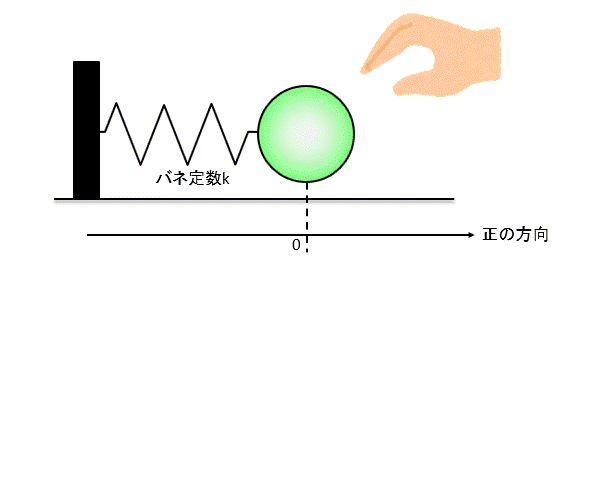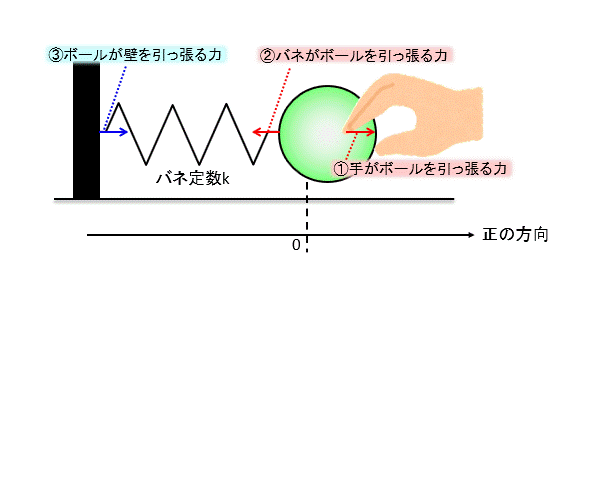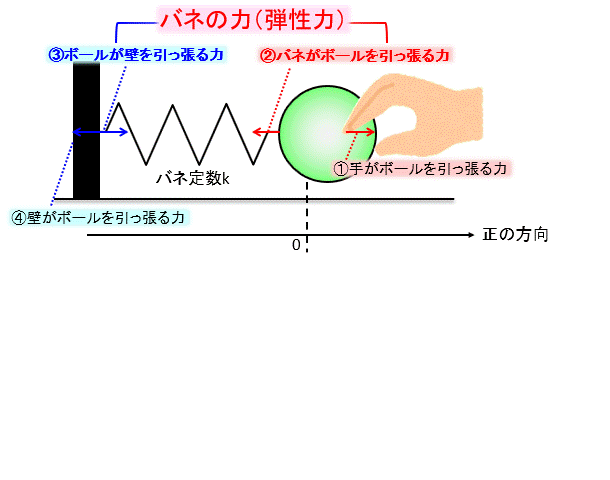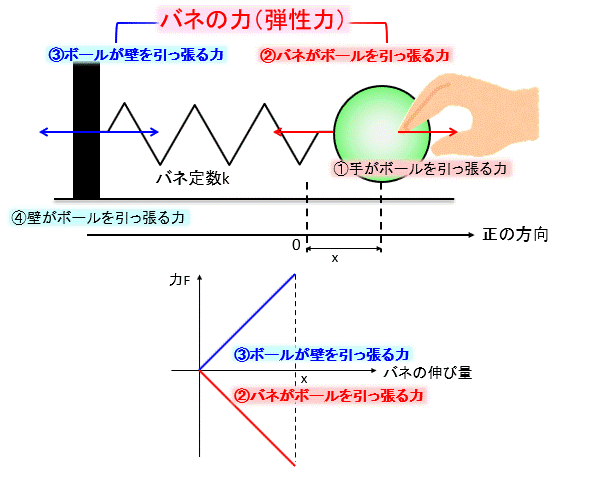
発生する力は、
①手がボールを引っ張る力
②バネがボールを引っ張る力
③バネが壁を引っ張る力
④壁に発生する反作用の力
①と②、③と④は作用反作用の関係にあります。
②と③がバネの弾性力(復元力ともいいます) なので、大きさは同じです。
これらから今回のケースでは①~④まで大きさは全て同じです。
※作用反作用の関係については過去記事を参考にしてください。
問題はバネの力の向きですが、②と③がバネの力で、それぞれ逆向きになっていますね。
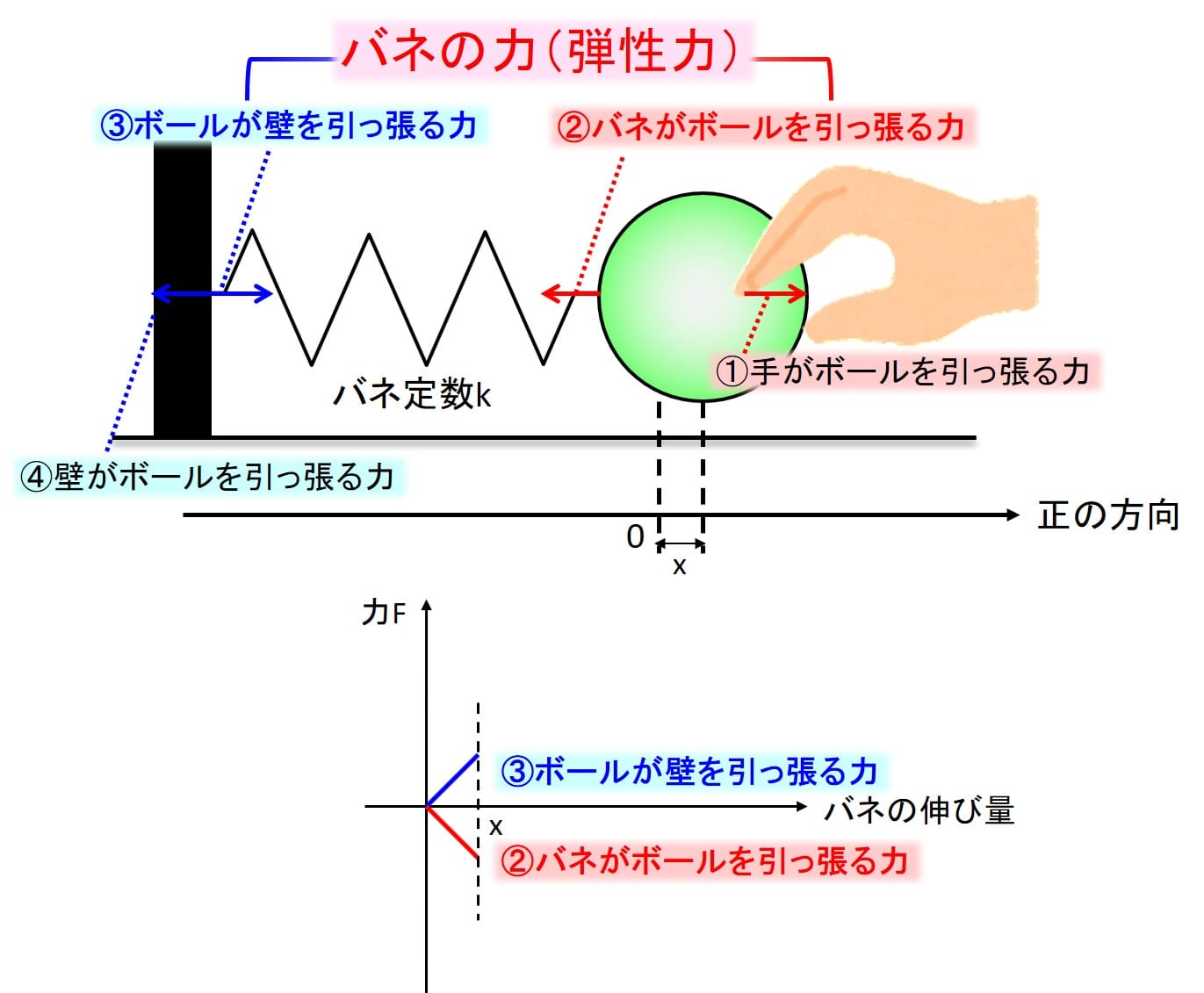
一般的にバネの力は?と聞かれたら、②のことを指すので、\(F=-kx\)と書くことが多いです。
でも反対側の壁に繋がっている力の③も厳密にはバネの力なのです。
ベクトル量だから単純にマイナスをつけておけばよい、ということをすると間違います。
バネの力とは、どこの力を指しているのか?を確実にとらえましょう。
その後、向きはどちらを正の方向に取っているかで決まります。
なぜ向きを間違うのか?マイナスは必要?
これは公式を理解できていないから、に尽きます。
フックの法則にしろ、公式は問題を解くための道具にすぎません。
ちゃんと道具の使い方を学びましょうということです。
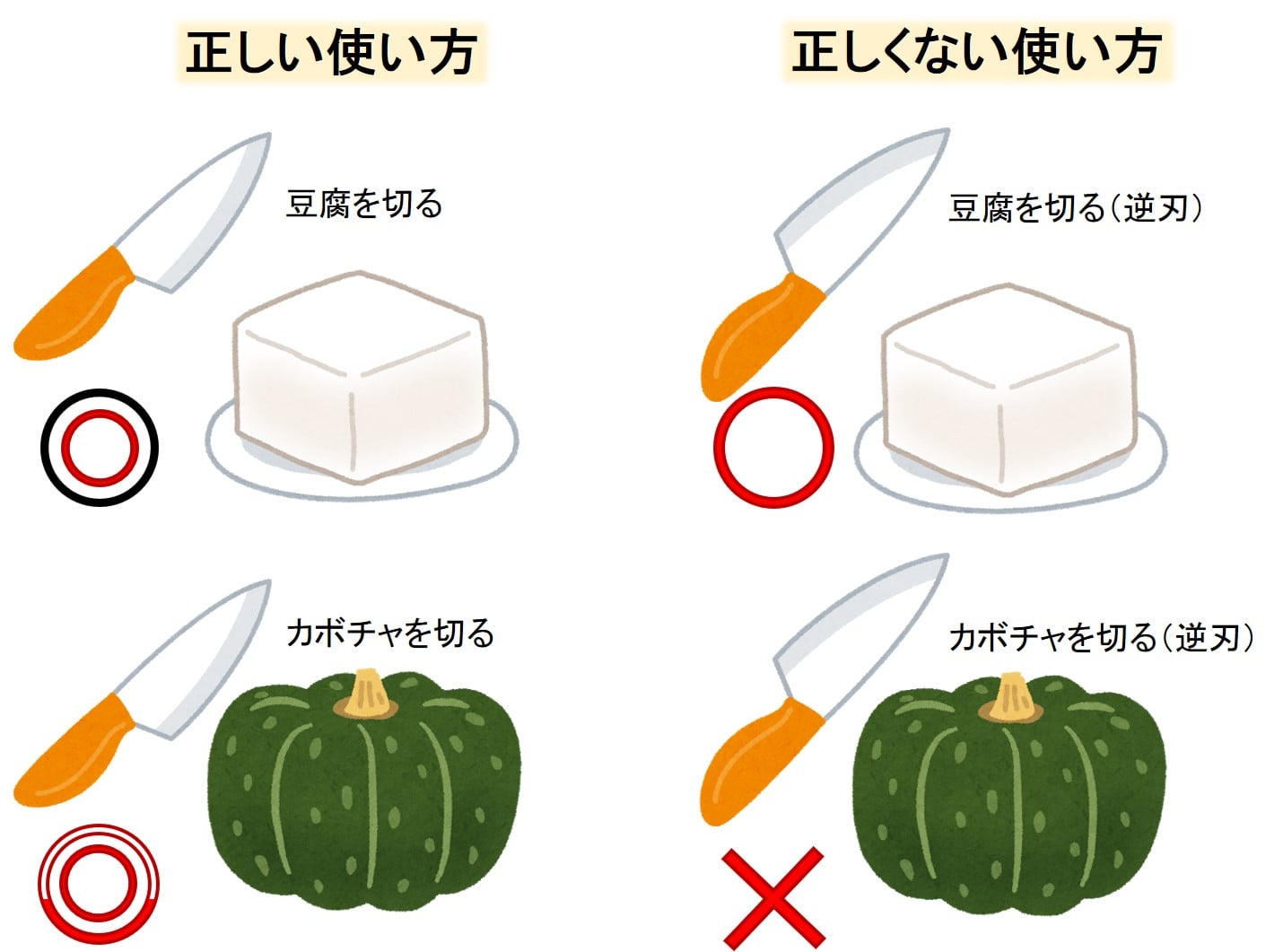
包丁を渡されて豆腐を切ってください、と言われたら、普通は刃の方で切りますが、
使い方を知らない子供だと刃ではない逆側で潰すように切るかもしれません。
豆腐だとどちらも切ることはできています。
でもカボチャを切るには逆側で切るのはなかなか難しいのではないでしょうか?
(難しくない、わたしマッチョだから★と言う人はごめんなさい。素直に謝ります)
ということで、フックの法則\(F=kx\)について深堀していきましょう。
フックの法則の表記
いろんな参考書やwebサイトで調べたところ、下記の2種類が多いです。
フックの法則の表記
- \(F=kx\)
- \(\boldsymbol{F}=-k\boldsymbol{x}\)
さっき説明した通り符号が違うだけじゃん!!


②の式をよく見てごらん。Fとxが太字になっているでしょ?これはベクトルを表しているんだ。
この①と②の区別ですが、 ①はスカラー量、②はベクトル量 で表されています。
つまり ①は向きは無視されている、②は向きが考慮されている 、ということです。
ここの違いをちゃんと理解していないと間違います。
①\(F=kx\)
これはスカラー量で表記されています。
つまり、『大きさだけ示していて、向きなんて関係ない』表記です。
xはバネの変位量なので、伸びようが縮もうが、変化した量が同じだったら大きさは同じです。
②\(\boldsymbol{F}=-k\boldsymbol{x}\)
こちらはベクトル表記です。
こう書かないといけないんだ!と主張するサイトが多いのですが、
これには注意してください。
先ほど示したとおり、バネの弾性力というのはバネの両端にかかる力を示しています。

上の図で説明すると、②と③のバネが引っ張る力です。
\(\boldsymbol{F}=-k\boldsymbol{x}\)が成立するのは②のバネがボールを引っ張るときだけです。
③のバネが壁を引っ張る力にはあてはまらないのです。
この\(\boldsymbol{F}=-k\boldsymbol{x}\)を使っている方は、②の場合に成り立つ、ということを肝に銘じておきましょう。
物理が得意な人はどちらを使っている?
私が接してきた勉強のできる10人(東大卒、阪大卒)たちは、9割が①の\(F=kx\)を使って、方向は後で考えていました。
こうやって書いてました。

みなさん口を揃えて、『後で見たら向きなんてわかるやん』と言ってました。
バネがいくつも繋がった複雑な問題を解くときに、\(\boldsymbol{F}=-k\boldsymbol{x}\)の公式に当てはめて解いていくと間違えるから嫌だ、とのことです。
これには私も大賛成です。
いろんな問題に応用が利くのは『大きさだけまず考えて、向きを後で決める』、という方法ですので、
物理を得意にしたい方にはおススメするやり方です。
バネの力と方向についてのまとめ
バネの問題のポイント
- 『バネの力は両端に発生する』
- 『バネの力の大きさはフックの法則、向きは図を見て判断』です。
間違いやすいポイントとして、フックの法則の符号について解説しました。
\(\boldsymbol{F}=-k\boldsymbol{x}\)というベクトルを使った考え方の場合、正の方向とどこのバネの力を指しているのかをしっかり意識しておきましょう。
フックの法則の拡張について
高校物理ではフックの法則=バネの力の法則と習うことが多いと思います。
しかし、大学で材料力学を学ぶと、バネの力以外にも適用できるように拡張することができます。
興味のある方は下記の記事を参考にしてください。