高校物理の力学　力の合成についてアニメーションで学ぼう

力のベクトルって分解だったり合成だったりできるって聞いたけど・・・よくわかんない。

苦手君

デルタ先生

力の分解や合成は、ベクトルの知識がどうしても必要になってくるから、詳しく解説するね。

今回は力の合成について解説します。

力のベクトルの基礎や、力の分解については過去の記事で解説していますので、参考にしてください。

本記事ではこんな人におススメです。

力の合成

ベクトルの基礎の復習

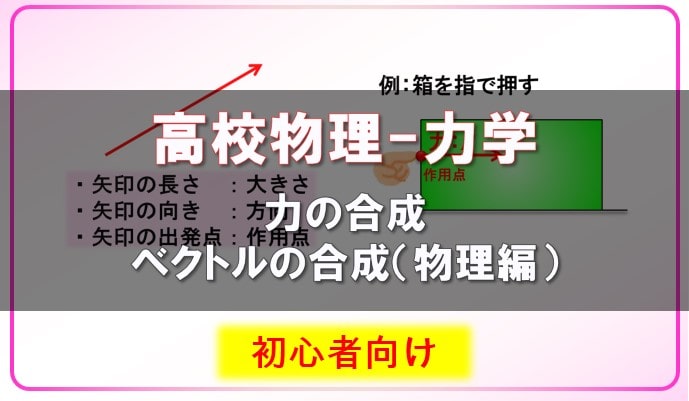
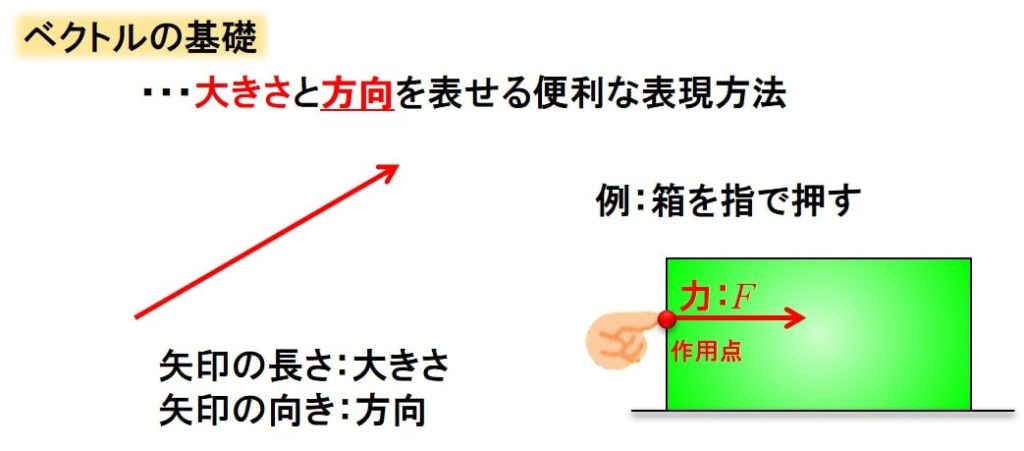
今まで力を矢印で書いてきましたが、これは数学でベクトルと呼んでいるものです。

ベクトルには、１とか２とか、ベクトル自体の大きさと、向きを表すことができます。

力のベクトルの場合、 作用点を出発点として、 力が発生している向きに矢印を書きます。

ベクトルの大事な考え方として、いろんな方向に分解したり、足し合わせたりできます。

今回はこのベクトルの合成についてです。

同じ向きの場合

まずは同じ向きを向いているベクトルの合成についてです。

結論、 単純に長さを足し合わせるだけでOKです。

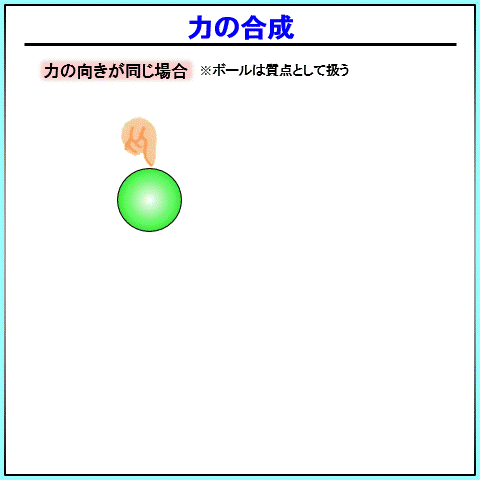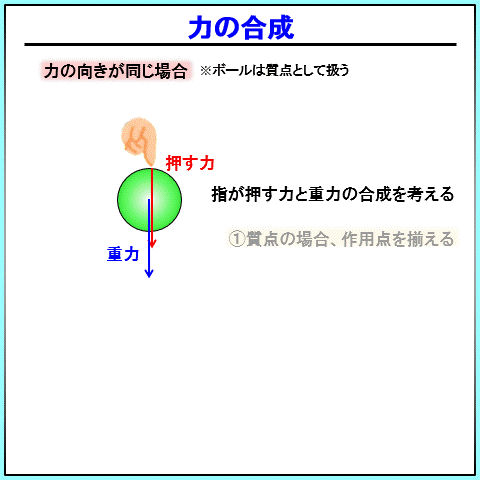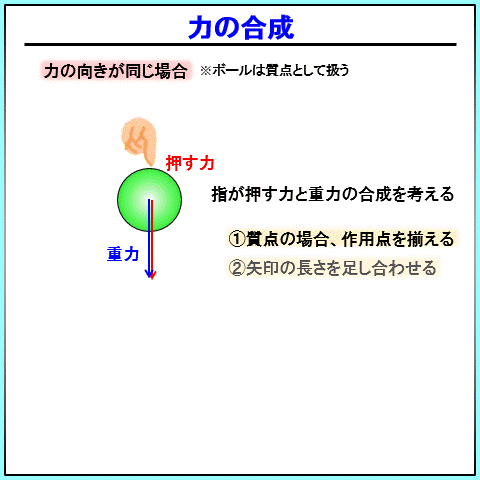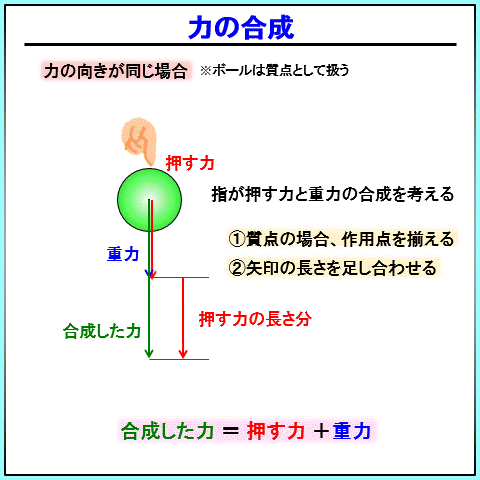
大事な考え方として 、質点を内の力で同じ向きの力は、作用点を平行移動させても大丈夫です。

これは質点自体には大きさが無いためです。

わかりやすいように、重力はボールの中央、指が押している点はボールの外周として書いていますが、大きさが無いのだから、同じ位置に持ってきても大丈夫、ということです。

大きさを考えるような問題（剛体の問題）では、単純に平行移動させると間違えますので、ご注意を。

あとは、二つの力のベクトルを足し合わせるだけです。

長さは、二つのベクトルの長さを足し合わせた長さになります。

今回の場合、押す力と重力の長さを足したものが、合成したベクトルになります。

向きが異なる場合

さて次は向きが異なる場合です。

3つのパターンを紹介します。

①180°向きが異なる場合

まず、180℃向きが異なる場合についてです。

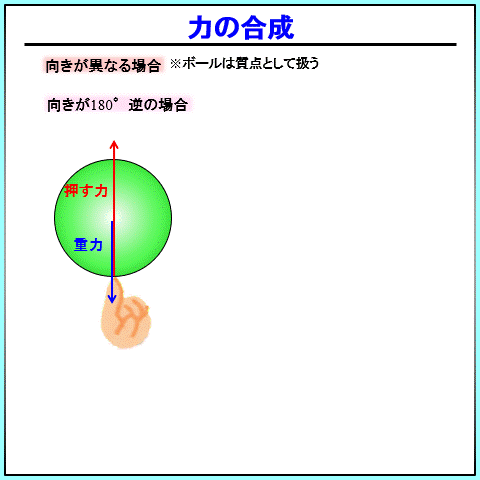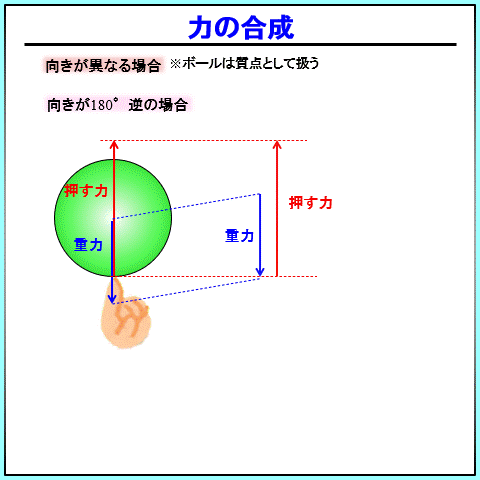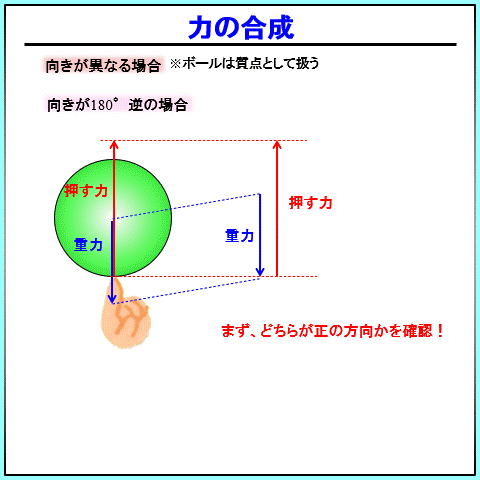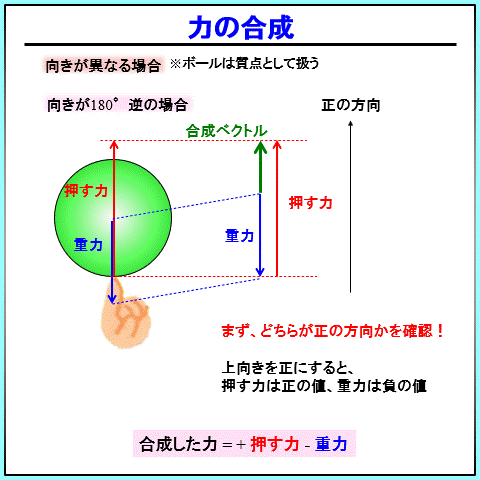
考え方は、同じ向きの合成とほぼ同じです。

矢印が逆向きになっているので、どちらかがプラス、どちらかがマイナスとなって和をとることになります。

どちらがプラスか、については、正の方向をどちらにとっているかを確認してください。

問題に指定されていなければ、自分で正の向きを設定しましょう。

例のように、正の向きを上向きにとると、上に押している力は正の方向、重力は負の方向になります。

合成すると緑の矢印のように押す力から、重力を引いた形で描かれます。

②、③向きが異なる場合（180°ではない）の合成

②と③のケース、2つのベクトルが一直線上で描かれない場合を考えます。

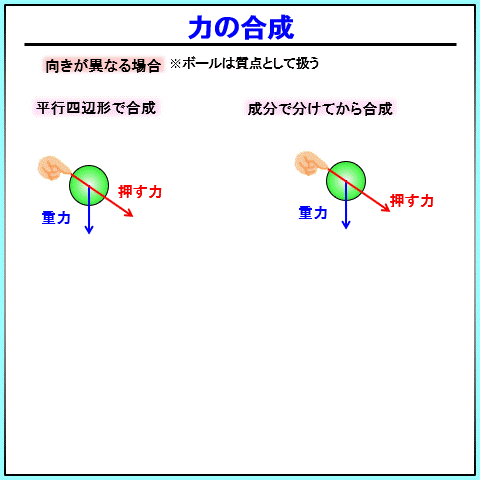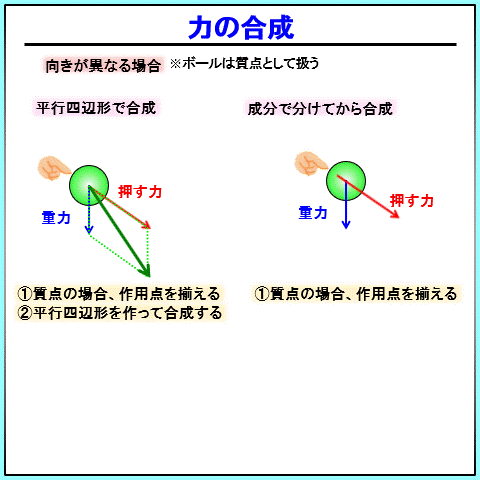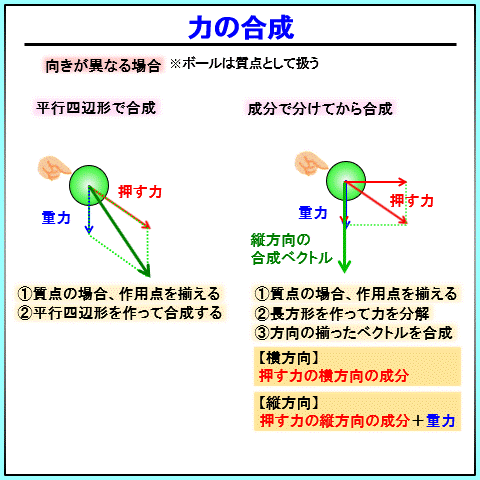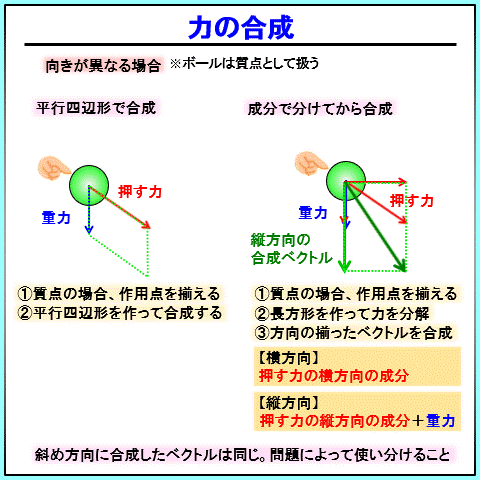
まず、質点の場合、作用点を揃えるのは同じです。

その後、 平行四辺形を作って、直接合成するのか、 斜めに向いているベクトルを無理やり分解して、方向をそろえて合成できる形にするか、です。

どちらを使うかは、ケースバイケースなのですが、

物理の問題を解く際には、斜めに向いているベクトルを一度分解して考えることが多いです。

まとめ

以上、力の合成でした。

今回、解説したのは大きさを無視できる質点系で、この場合、力の作用点を質点上でそろえて考えることを忘れないようにしましょう。

同じ向きを向いているベクトルの場合、単純に足し合わせるだけでOKです。

向きが異なる場合、3つのパターンを解説しました。

180°異なる場合は、正の方向に注意して足し合わせるだけでOKです。

一直線上に無い場合は、

平行四辺形を作って合成するか、

長方形を作り成分ごとにわけて、同じ方向のベクトルを足し合わせるか、です。

できるだけ多くの問題を解いて、ベクトルの扱いに慣れましょう。

ベクトルは物理を理解するための道具です。

道具は使い方を知っててもちゃんと使いこなすまで練習しなければ、使えません。

しっかり理解した上で、練習する、地道ですがこれが一番の近道ですので、がんばりましょう！

デルタ先生

実際に、問題を解いて自分のモノにしてね！日々の勉強頑張ってください☆ありがとうございました！