振動・波動の基礎-⑰多自由度の振動の運動方程式をわかりやすく解説！行列を使って表現

多自由度の振動ってこれまでの2自由度の場合と解き方は同じなの？

苦手君

デルタ先生

基本的には同じだよ。行列を利用して運動方程式を立てればいいんだ。

これまで1自由度、2自由度の振動について勉強してきました。

今回は自由度を上げて3自由度以上の場合を含んだ、多自由度の振動系を解説します。

多自由度系の振動は、CAE（Computer aided engineering）の分野でよく使われます。

こういったシミュレーション解析では、パラメータさえ入れてしまえば結果が出てくるので、運動方程式の中身などを知らなくてよい、

と考えてしまう人がたまにいらっしゃいますが、これはよろしくないです。

中身をしっかりと理解していないと、出てきた答えの考察や判断を間違うことが多々ありますので、しっかり理解しておきましょう。

過去に2自由度の振動について解説していますので参考にしてください。

過去記事

振動・波動の基礎-⑦2自由度系の運動方程式行列表現を使って見やすくしよう

振動・波動の基礎-⑯2自由度の連成振動（減衰無し、質量とバネ定数が同じ場合）

本記事をおススメする人

多自由度の振動を勉強している人
物理を勉強していて興味がある人、仕事で振動の知識を使う人

動画でも解説していますので、是非下記動画も参考にしていただければと思います。

多自由度振動系

多自由度の連成振動のモデル

今回は簡単のために連成振動のモデルで考えます。

下図のように両端の質点がバネで固定端と繋がっている状態です。

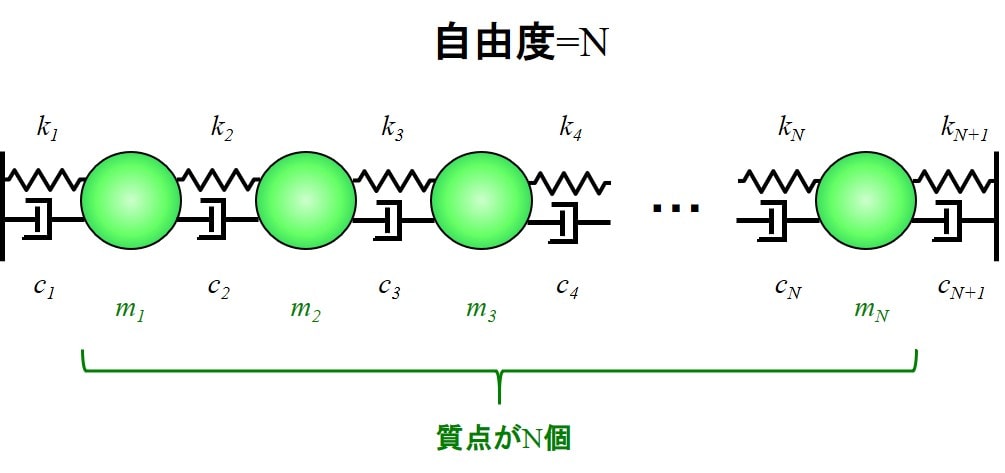
$N$個の質点が$N+1$個のバネとダンパーに繋がれています。

$i=1,2,3,・・・,N$として、

$m_i$:$i$番目の質点の質量

$k_i$:$i$番目のバネのバネ定数

$c_i$:i番目のダンパーの減衰係数

$x_i$:$i$番目の質点の位置

と表しています。

運動方程式

では、運動方程式を立てましょう。

1自由度の時は質点が1個だったので、運動方程式は1個だけでしたね。

2自由度の時は質点が2個だったので、2個の運動方程式を作ることができました。

運動方程式は質点1つに対して1つ作ることができますので、今回のケースだと、質点がN個ありますので、運動方程式もN個つくることができます。

N個ってN=100とかだったらどうするの？100個も運動方程式つくれないよ！

苦手君

デルタ先生

大丈夫、こういう連成振動の場合であれば100個でもN個でも作ることができるよ。

1個目の質点の運動方程式

まず、左から数えて1個目の質点についての運動方程式を作ってみましょう。

質点にかかっている力はバネとダンパーから受ける力になります。

右向きを正の方向として、以下考えていきます。

1個目のバネの力は$-k_1x_1$、2個目のバネの力は$-k_2x_1+k_2x_2$となります。

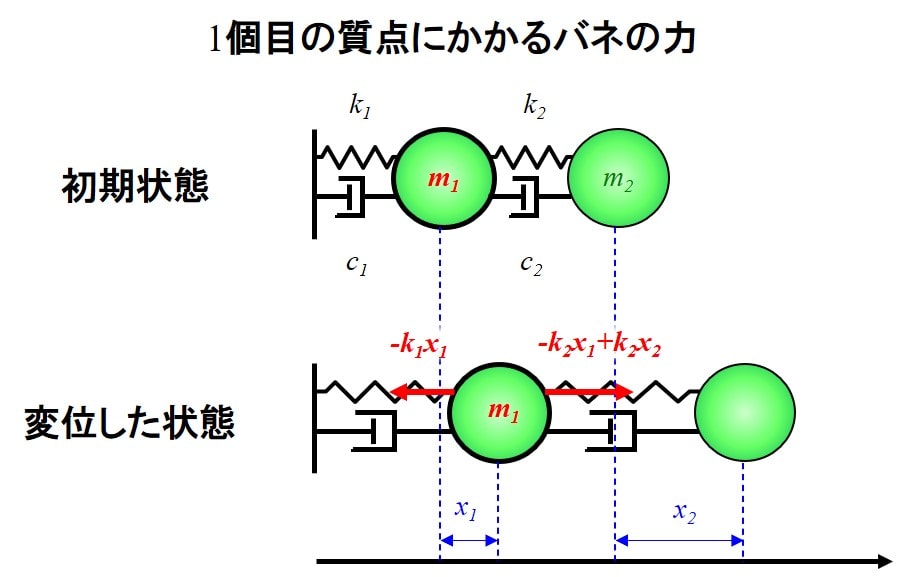
1つお隣の２個目の質点の変位も考える必要があることに注意が必要です。

1個目のダンパーから受ける力は$-c_1\dot{x}_1$、2個目のバネの力は$-c_2\dot{x}_1+c_2\dot{x}_2$となります。

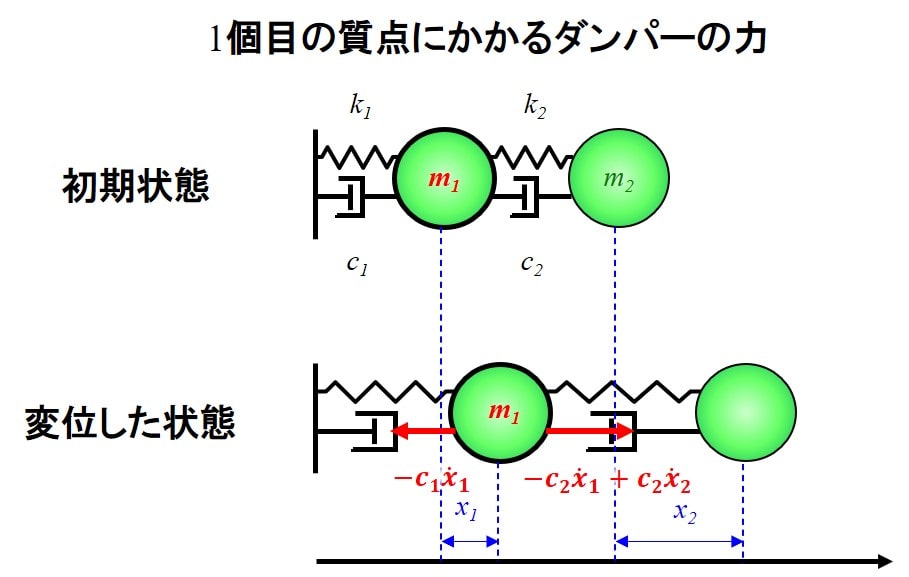
運動方程式はこれらのバネの力とダンパーからの力を用いて、下記のようになります。

$$m_1\ddot{x}_1 = -k_1x_1-k_2x_1+k_2x_2-c_1\dot{x}_1-c_2\dot{x}_1+c_2\dot{x}_2$$

これで１個目の質点の運動方程式ができました。

２個目の質点の運動方程式

続いて左から２個目の運動方程式を考えます。

１個目と同じように、バネとダンパーから受ける力を考えましょう。

２個目の質点につながっているのは、２個目と３個目のバネとダンパーなので、それぞれの力を見ていきます。

２個目のバネの力は、１個目の質点の変位も考える必要があるので、$-k_2x_2+k_2x_1$です。

３個目のバネの力は、$-k_3x_2+k_3x_3$ですね。

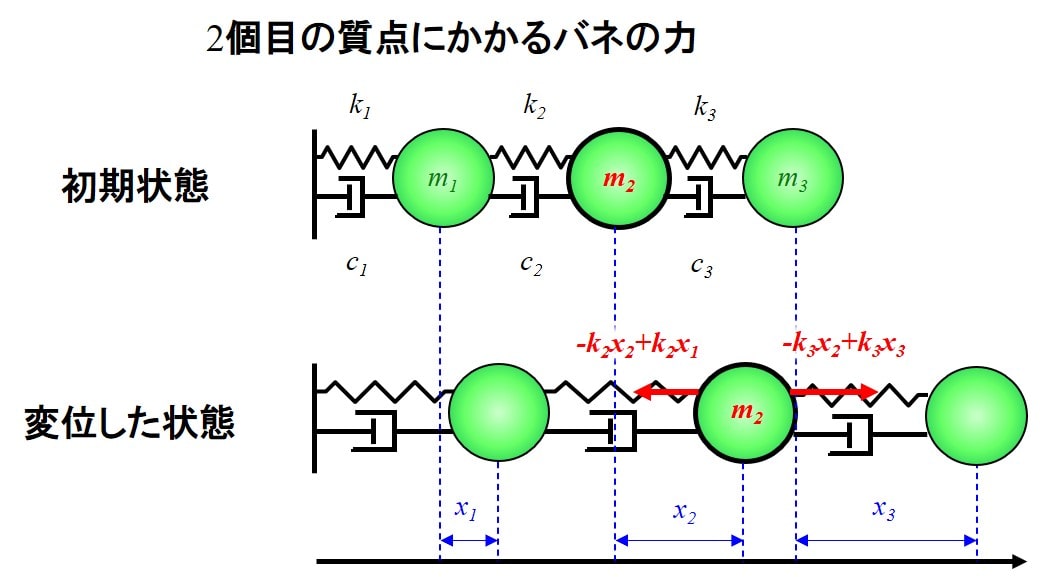
次にダンパーですが、２個目のダンパーから受ける力は、$-c_2\dot{x}_2+c_2\dot{x}_1$となります。

３個目のダンパーの力は、

$$-c_3\dot{x}_2+c_3\dot{x}_3$$ですね。

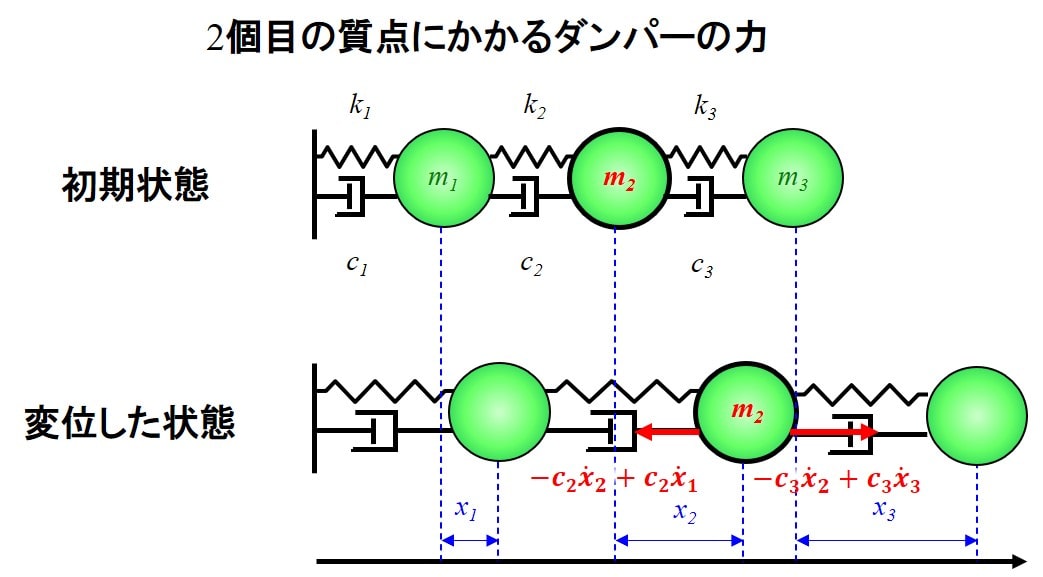
以上から、２個目の運動方程式は下記のようになります。

$$m_2\ddot{x}_2 = -k_2x_2+k_2x_1-k_3x_2+k_3x_3-c_2\dot{x}_3+c_2\dot{x}_2-c_3\dot{x}_2+c_3\dot{x}_3$$

3個目の質点の運動方程式

では3個目に行きましょう。

3個目は完全に2個目と同じになります。

3個目のバネの力は、$-k_3x_3+k_3x_2$です。

4個目のバネの力は、$-k_4x_3+k_4x_4$ですね。

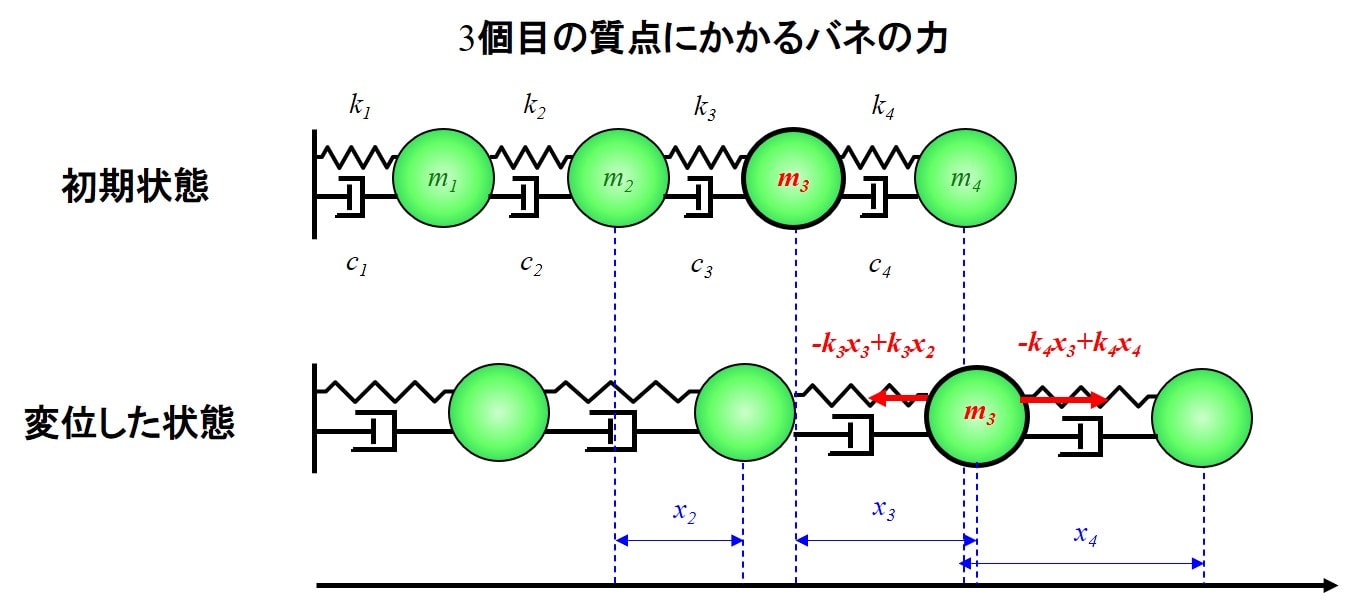
次にダンパーですが、3個目のダンパーから受ける力は、$-c_3\dot{x}_3+c_3\dot{x}_2$となります。

4個目のダンパーの力は、$-c_4\dot{x}_3+c_4\dot{x}_4$ですね。

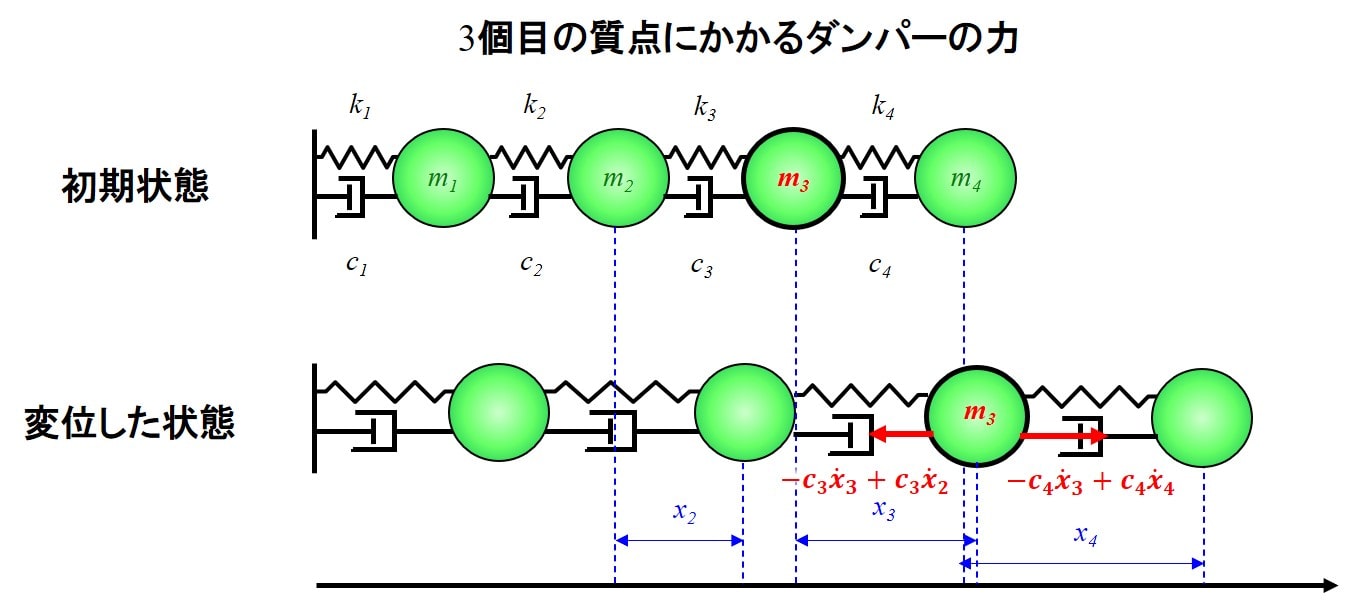
以上から、3個目の運動方程式は下記のようになります。

$$m_3\ddot{x}_3 = -k_3x_3+k_3x_2-k_4x_3+k_4x_4-c_3\dot{x}_3+c_3\dot{x}_2-c_4\dot{x}_3+c_4\dot{x}_4$$

i個目の質点の運動方程式

具体的に１個目から３個目まで運動方程式を立ててきましたので、

ここで$i=1,2,3…N$として、適当な$i$番目の部分だけ切り取って、$i$番目の運動方程式を考えましょう。

これも２個目以降の話と全く同じ考え方でOKです。

$i$個目の質点は、下図のように、$i$番目、$i+1$番目のバネとダンパーにつながれています。

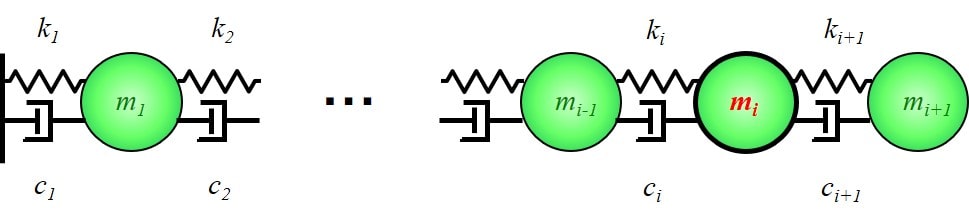
$i$番目、$i+1$番目のバネとダンパーからの力を書き出してみましょう。

$i$番目のバネから受ける力は、$-k_ix_i+k_ix_{i-1}$となりますね。

$i+1$番目のバネから受ける力は、$-k_{i+1}x_i+k_{i+1}x_{i+1}$です。

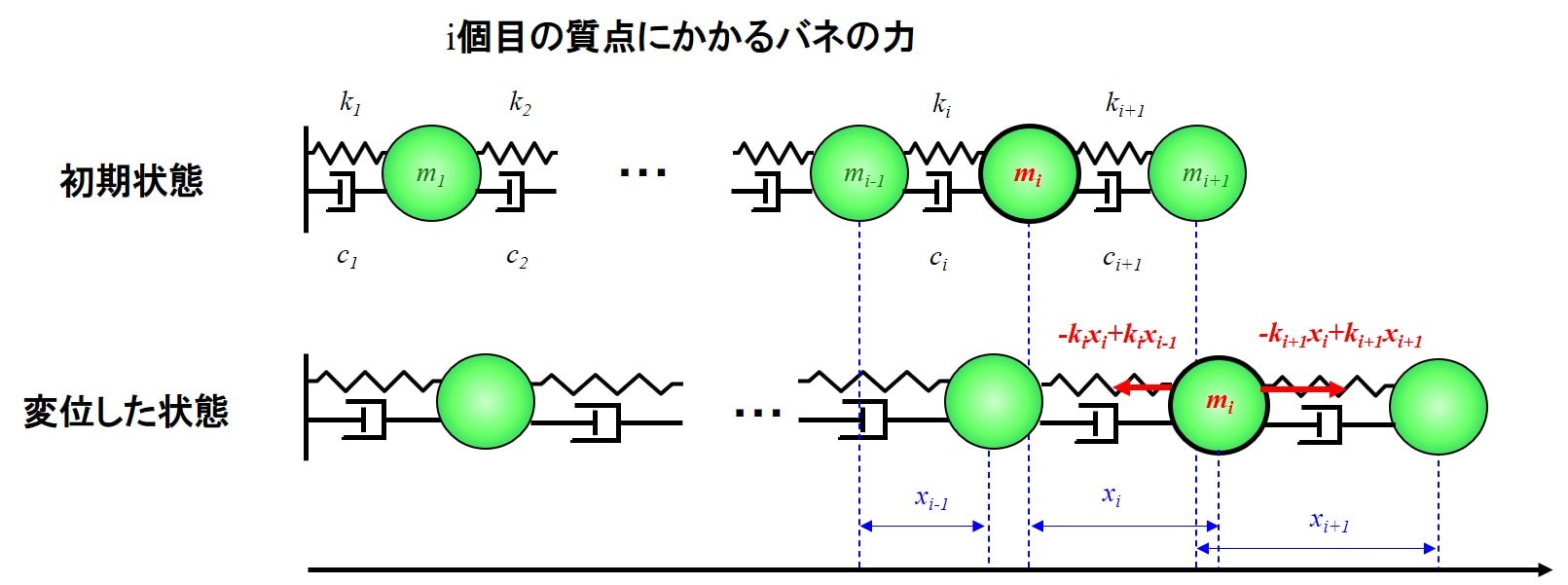
続いて、ダンパーです。$i$番目のダンパーから受ける力は、$-c_i\dot{x}_i+c_i\dot{x}_{i-1}$、

$i+1$番目のダンパーから受ける力は、$-c_{i+1}\dot{x}_i+c_{i+1}\dot{x}_{i+1}$となります。

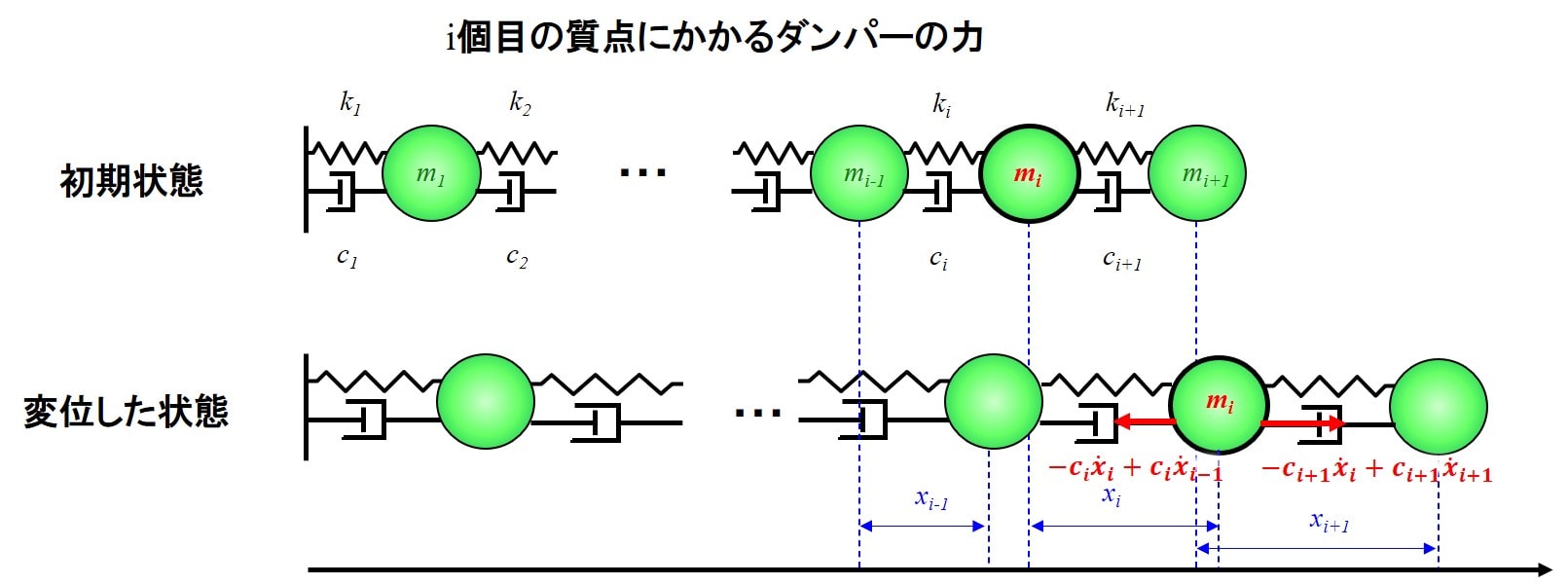
以上から運動方程式は、

$$m_i\ddot{x}_i = -k_ix_i+k_ix_{i-1}-k_ix_i+k_{i+1}x_{i+1}-c_i\dot{x}_i+c_i\dot{x}_{i-1}-c_{i+1}\dot{x}_i+c_{i+1}\dot{x}_{i+1}$$

これを少し整理して、

$$m_i\ddot{x}_i -c_i\dot{x}_{i-1}+(c_i+c_{i+1})\dot{x}_i-c_{i+1}\dot{x}_{i+1}-k_ix_{i-1}+(k_i+k_{i+1})x_i-k_{i+1}x_{i+1}=0 $$

これで$i$番目の運動方程式が求まりました。

ちなみに$i=1$や$i=N$のとき、$x_0$や$x_{N+1}$など、存在してはいけない添え字のパラメータが表れてしまいますが、

これらをすべてゼロとしてしまえば、$i=1,2,3・・・N$に対応した運動方程式になります。

試しに$i=1$の時、$x_0$や$\dot{x}_0$が表れてしまいますが、これらをゼロとして扱うと、１個目の質点のときに求めた運動方程式と全く同じ式を得ることができます。

運動方程式を行列で書く

では、運動方程式を書いていくのですが、N行N列の行列を用いて表現します。

質量mに関するN行N列の行列、質量マトリックス$M$と、加速度のベクトル$\ddot{X}$として、下記のようにすると、$MX$で表すことができます。

$$M=\left(\begin{array}{cccc}m_1&0&\cdots&0\\0&m_2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&m_N\end{array}\right)$$

$$\ddot{X} = \left(\begin{array}{c}\ddot{x}_1\\\ddot{x}_2\\\vdots\\\ddot{x}_N\end{array}\right)$$

次に右辺ですが、これはバネの部分とダンパーの部分とでわけて考えて行列で表します。

バネのマトリックスを$K$、ダンパーのマトリックスを$C$とすると、

$$K=\left(\begin{array}{cccc}k_1+k_2&-k_2&\cdots&0\\-k_2&k_2+k_3&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&k_N+k_{N+1}\end{array}\right)$$

$$C=\left(\begin{array}{cccc}c_1+c_2&-c_2&\cdots&0\\-c_2&c_2+c_3&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&c_N+c_{N+1}\end{array}\right)$$

速度と位置のベクトルを$\dot{X}$、$X$とすると、

$$\dot{X} = \left(\begin{array}{c}\dot{x}_1\\\dot{x}_2\\\vdots\\\dot{x}_N\end{array}\right)$$

$$X = \left(\begin{array}{c}x_1\\x_2\\\vdots\\x_N\end{array}\right)$$

運動方程式は以上を用いて、

$$M\ddot{X}+C\dot{X}+KX=0$$

と表すことができます。

これで運動方程式が求まりました。

まとめ

N自由度系の振動の運動方程式を求めました。

行列が苦手な人は少し苦労するかもしれませんが、具体的に１個ずつ考えて、一般化する（i番目を考える）、という手順でゆっくりでもよいので、順番に理解していきましょう。

参考文献

振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

本サイトの振動工学のページはこちら。

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 →振動・波動の基礎-⑳固有振動モードを導出する！多自由度の自由振動-減衰なし