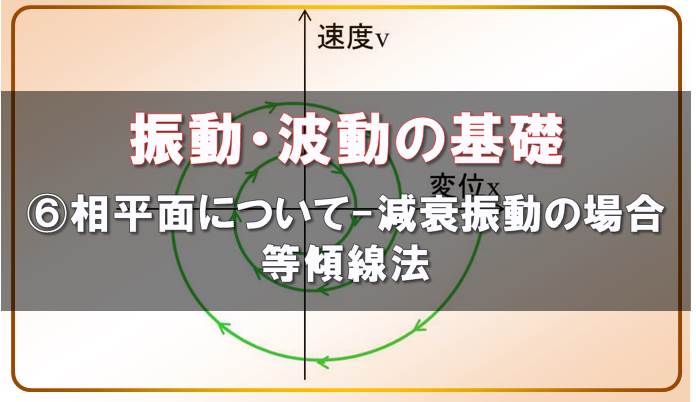
今度は相平面でうずまきみたいになっているんだけど…


単振動の場合は、おなじ楕円をグルグル回るんだけど、減衰がある場合はうずまき状になるんだ。
本日は相平面の減衰振動の場合について説明します。
前回の単振動の場合については下記の過去記事を参考にしてください。
本記事ではアニメーションを入れて、イメージがつくように解説します。
本記事をおススメする人
- 単振動の場合と減衰振動の場合の相平面の違いがわからない人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
最初に減衰アリの相平面の図を下に示しますね。
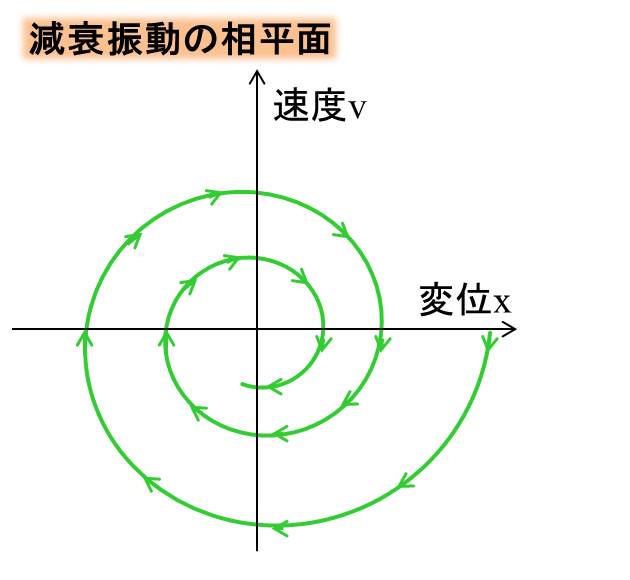
それでは、単振動の場合の復習をして、減衰アリの相平面まで理解していきましょう。
下記動画でも解説していますので、是非参考にしていただければと思います。
相平面の復習
簡単に言うと、 横軸を変位、縦軸を速さとして、振動を表現したもの、になります。
単振動の場合の例を下記に示します。
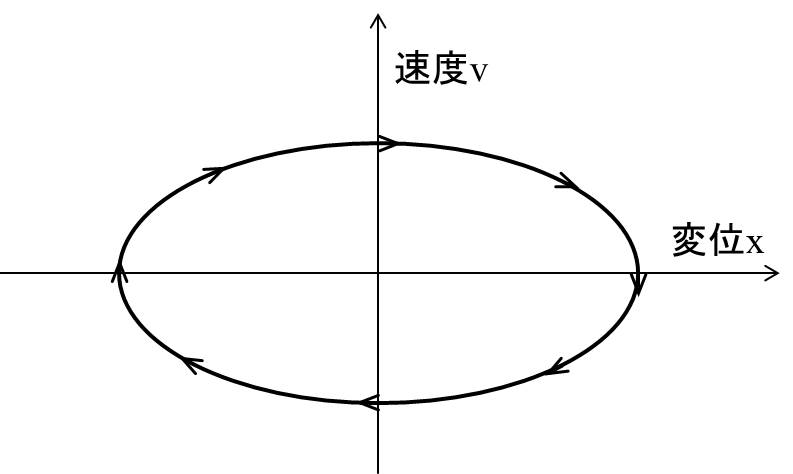
矢印のある線を『 軌道』と言います。
注意すべき点は、 時間軸の概念がない、という点です。
減衰振動の相平面
今回は減衰のある自由振動を考えます。
減衰振動についての詳細は下記の過去記事を参考にしてください。
参考記事
減衰振動のモデル
さて、減衰振動のモデルは下記のように、質量\(m\)にバネと減衰部分(ダンパーやダッシュポットと呼びます)がくっついたモデルで示せます。
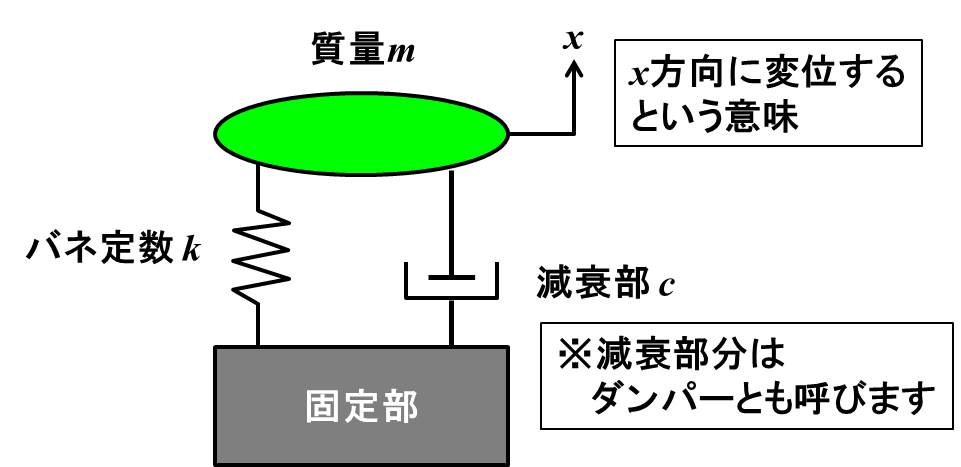
バネ定数\(k\)は梁の硬さと同じ意味を示します。
\(c\)は減衰の大きさを示す減衰係数というパラメータです。
減衰が物体の速度に比例して大きくなる、という粘性減衰を仮定しています。
この減衰を考慮した場合の運動方程式は下記のようになります。
両辺を\(m\)で割って、ζとωというパラメータを下のように定義すると、運動方程式は、
ζは減衰比、ωは固有振動数を示します。
さて、この運動方程式の相平面を考えましょう。
相平面の描き方
等傾線法(isocline-method)
これは教科書的によく説明されている方法でもあります。
思想としては、 xとvの傾きからグラフを描く、という考え方です。
\(x\)と\(v\)の傾き、つまり\(\frac{dv}{dx}\)の式からグラフを描く、ということですね。
ということで、運動方程式を式変形して、\(\frac{dv}{dx}\)を導き出しましょう。
まず、\(x\)の時間微分については、下記のように書き換えられます。
$$\dot{x} = \frac{dx}{dt} = v・・・②$$
$$\ddot{x} = \frac{dv}{dt}・・・③$$
①の運動方程式に②と③を代入すると、
整理すると、
今、導出したいのは$\frac{dv}{dx}$で、②と④式の左辺をよ~く見ると、分母の\(dt\)が邪魔ですね。
④÷②とすると、\(dt\)が消えて、\(\frac{dv}{dx}\)が左辺に残ってくれますので、割りましょう。
$$\frac{dv}{dx} = \frac{-2ζωv-x}{v}・・・⑤$$
この式から、相平面上の\(x\)と\(v\)が定まると傾きが求まる、ということがわかりますね。
\(\frac{dv}{dx}=m\)とわかりやすい定数\(m\)という形で傾きを表すと、
$$m = \frac{-2ζωv-x}{v}$$
変形して、
$$v=\frac{-1}{2ζω+m}・x・・・⑥$$
これは、傾き\(m\)の軌跡が⑥式で表されるということを意味しています。
具体例として\(m=1\)の時を考えてみましょう。
$$v=\frac{-1}{2ζω+1}・x$$
この式をグラフに書くと下記のようになります。
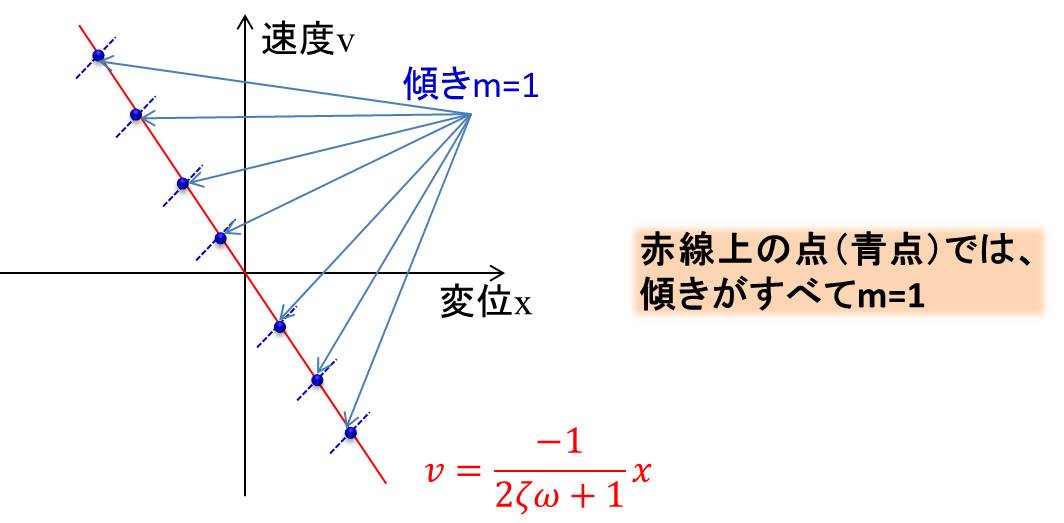
赤の線が傾き\(m=1\)の時の\(x\)と\(v\)の軌跡を示していて、その線上では、傾きが常に\(m=1\)となっています。
同様に、\(m=0、m=-1\)などのほかの\(m\)の値も入れると下記のようになります。
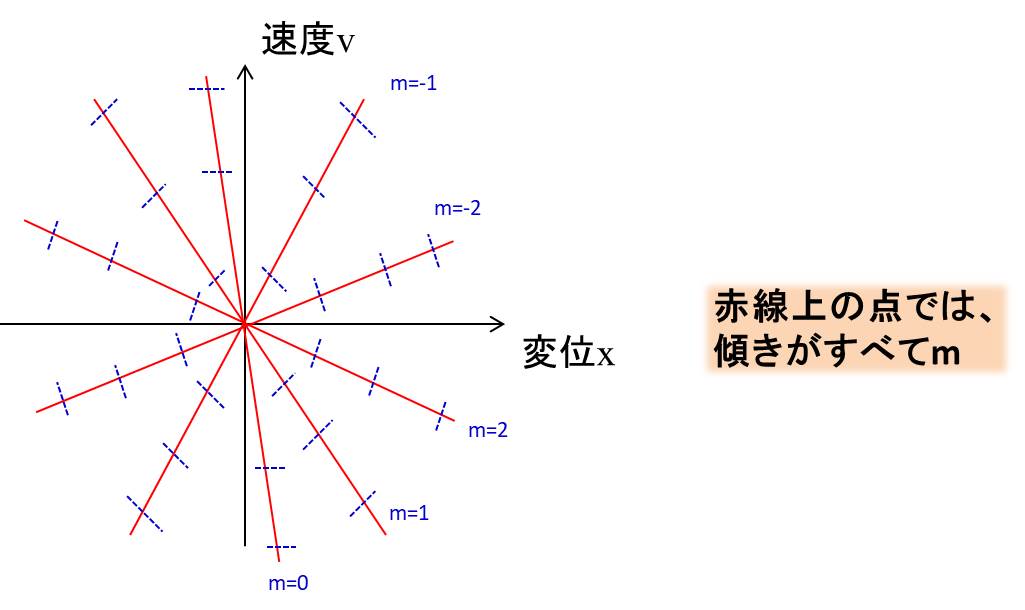
あとは初期値を考えましょう。
初期の変位を\(x_0\)、自由振動なので、初期の速度は0です。
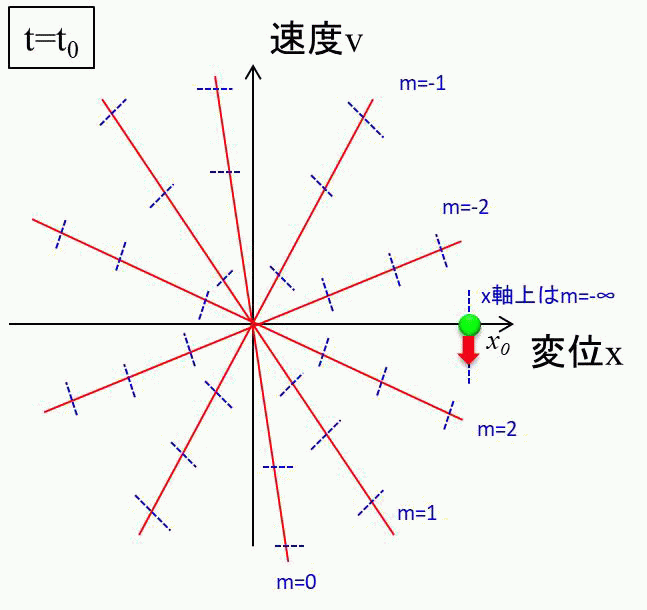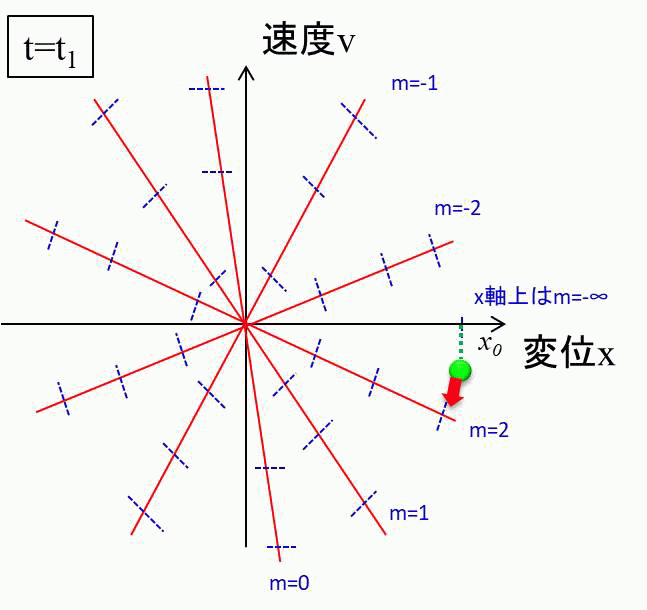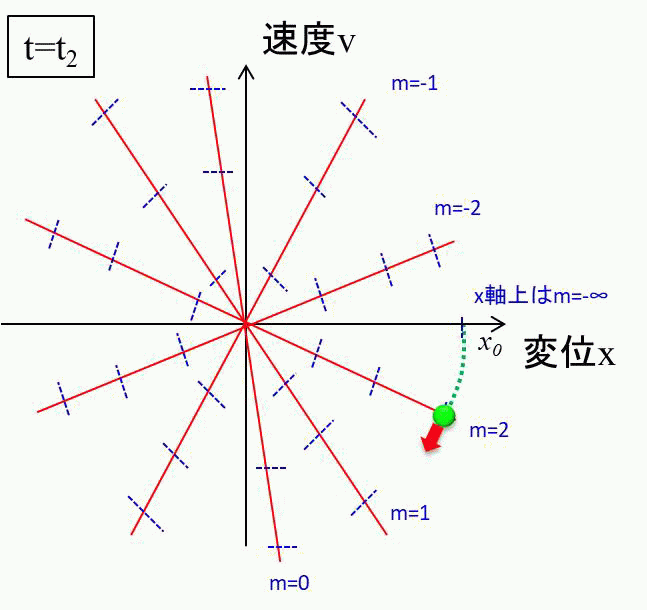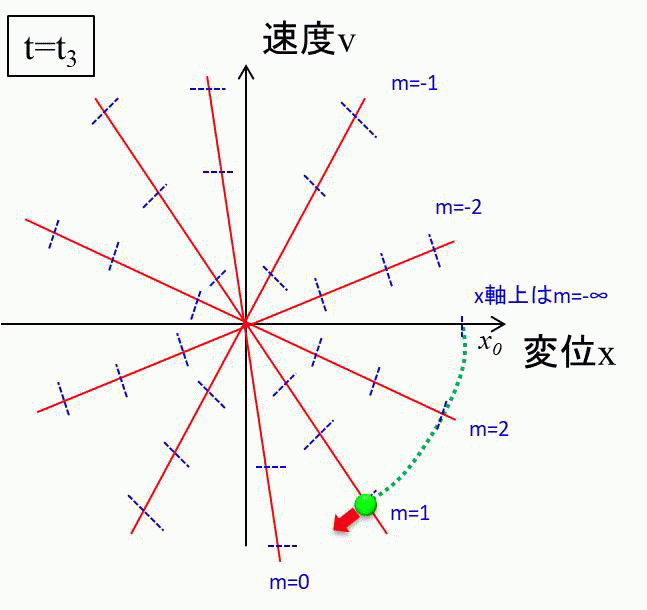
ということで、初期値は\(x\)軸上の点\((x_0,0)\)になります。
\(v=0\)のときの傾き\(m\)は-∞になりますので、相平面上の最初の動きは、" 初期位置から真下へ移動"となります。
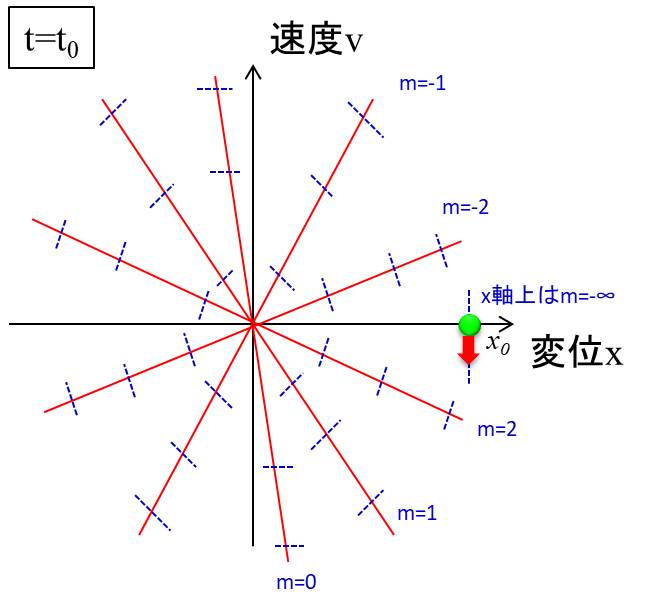
少し下に点がずれると、正の傾きを持つので、徐々に左下へ弧を描いて移動します。
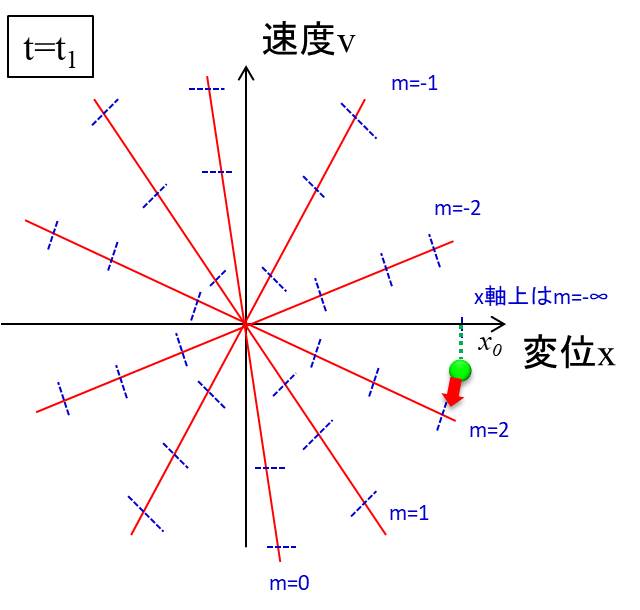
さて、\(m=0\)の線ですが、これが縦軸である\(v\)軸と少しずれていることに気が付いたでしょうか?
単振動の場合、\(ζ=0\)なので、⑤式において、
$$\frac{dv}{dx} = m = \frac{-2ζωv-x}{v}・・・⑤$$
これに代入すると、\(m=\frac{-x}{v}=0\)となり、x=0となります。
つまり、\(m=0\)の軌跡は\(v\)軸と一致するのですが、減衰項があるため、縦軸と少しずれる、ということですね。
この減衰項がある結果、相平面上の物体の軌跡はグルグルとうずまくような形になります。
等傾線法は慣れないと少し理解が難しいかもしれませんので、もう少しイメージ持ちやすくするために、グラフから見てみましょう。
変位と速度のグラフからイメージ
簡単のために、変位と速度の時間の式を下記のように表します。
$$x=Acosωt$$
$$v=\frac{dx}{dt}=-A'sinωt$$
\(A、A'\)は減衰を含む振幅です。(A'は単純にAを時間微分したものではないので注意してください)
これらのグラフを使って、相平面上をどのように動くか見てみましょう。
まず、相平面の右側に、変位と速度の時間推移のグラフを置きます。
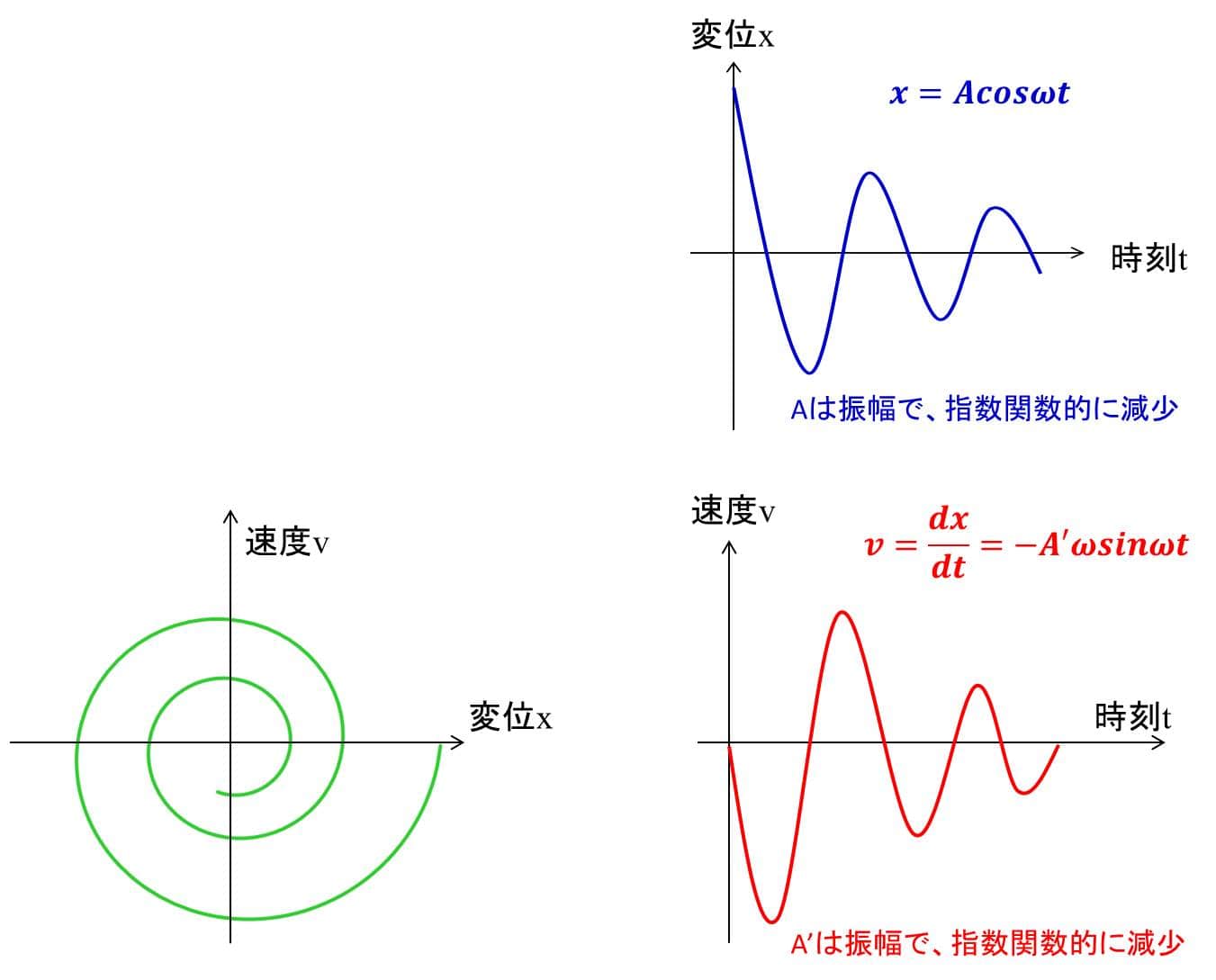
変位のグラフを90°回転させます。
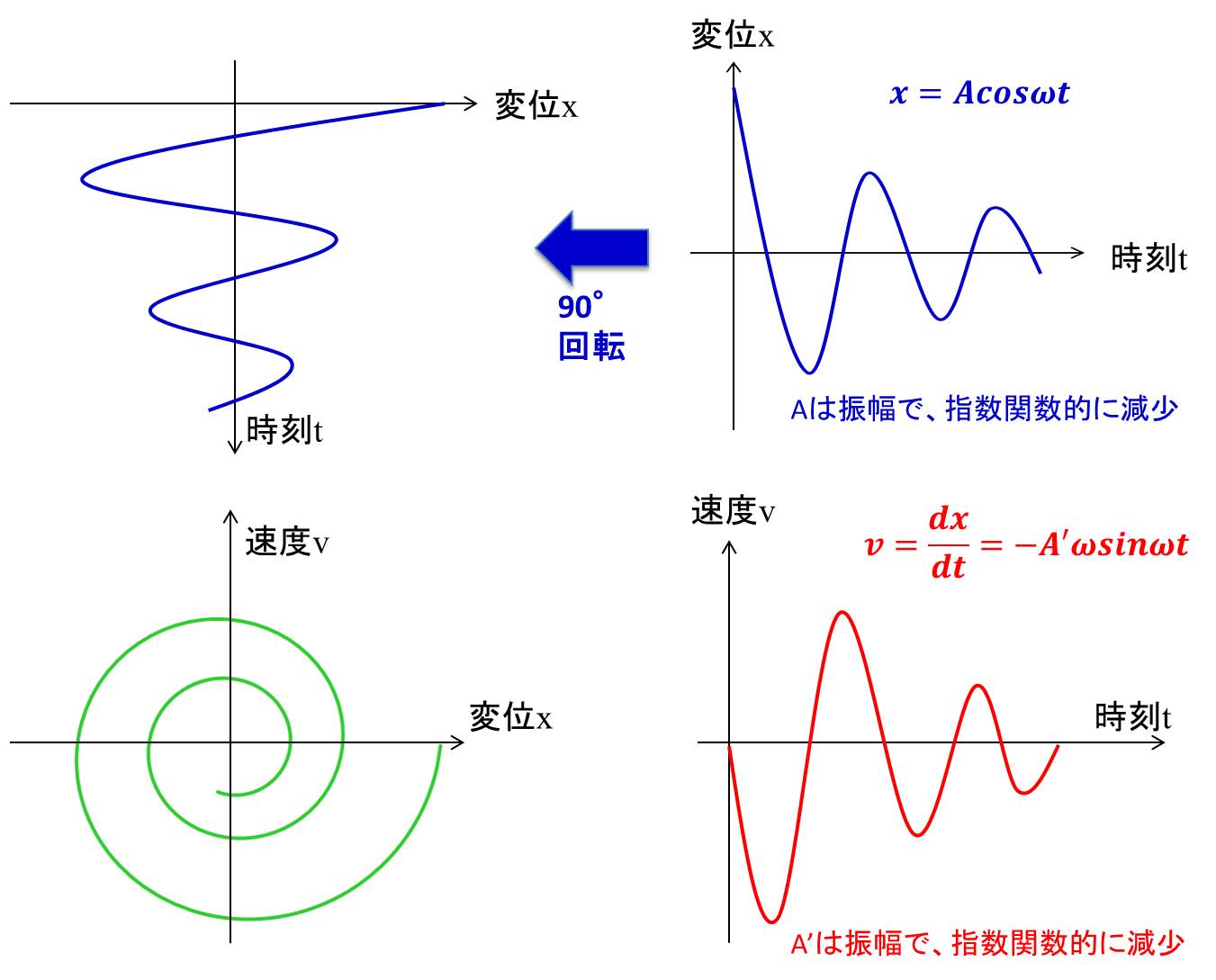
それでは初期値からグラフを動かしてみましょう。
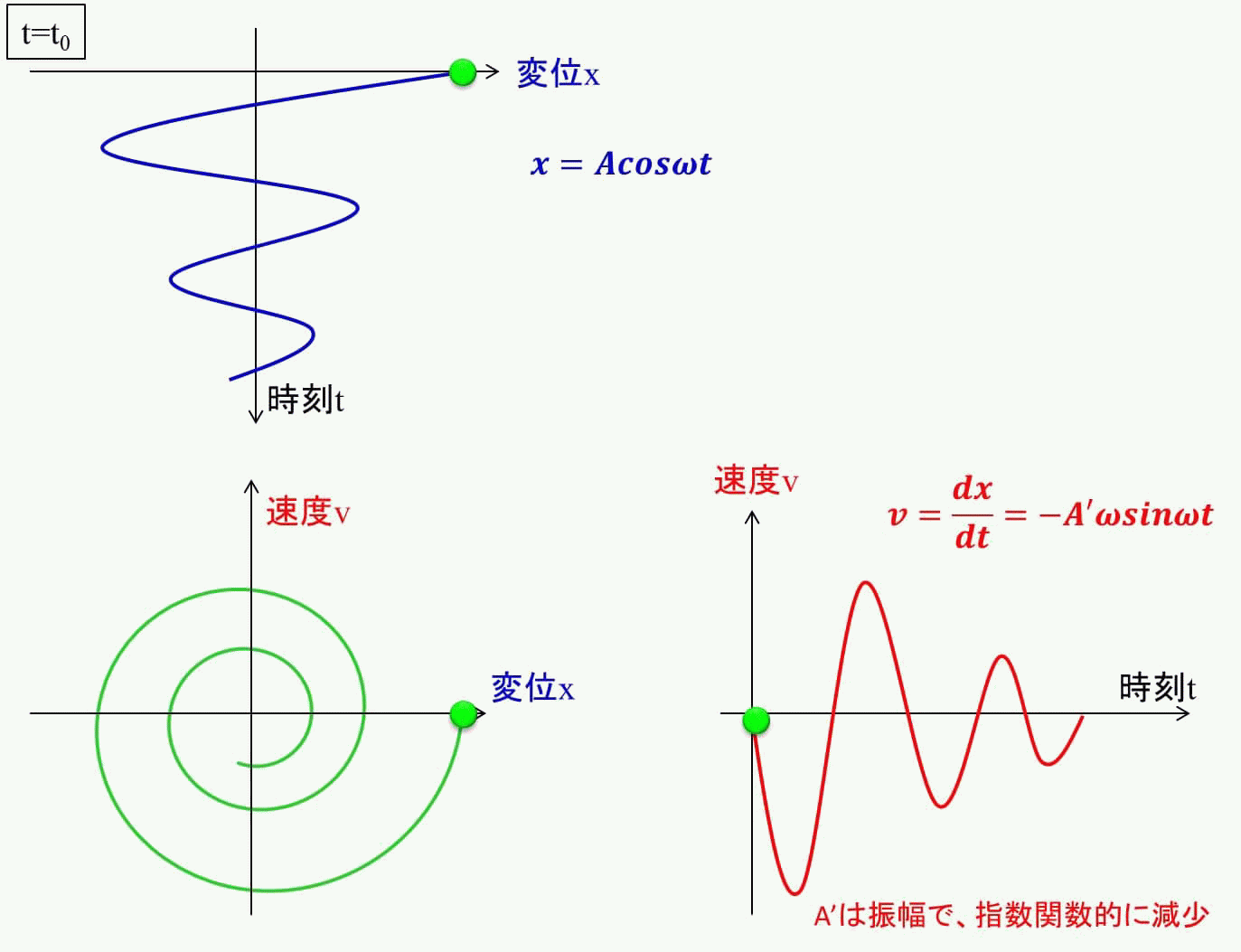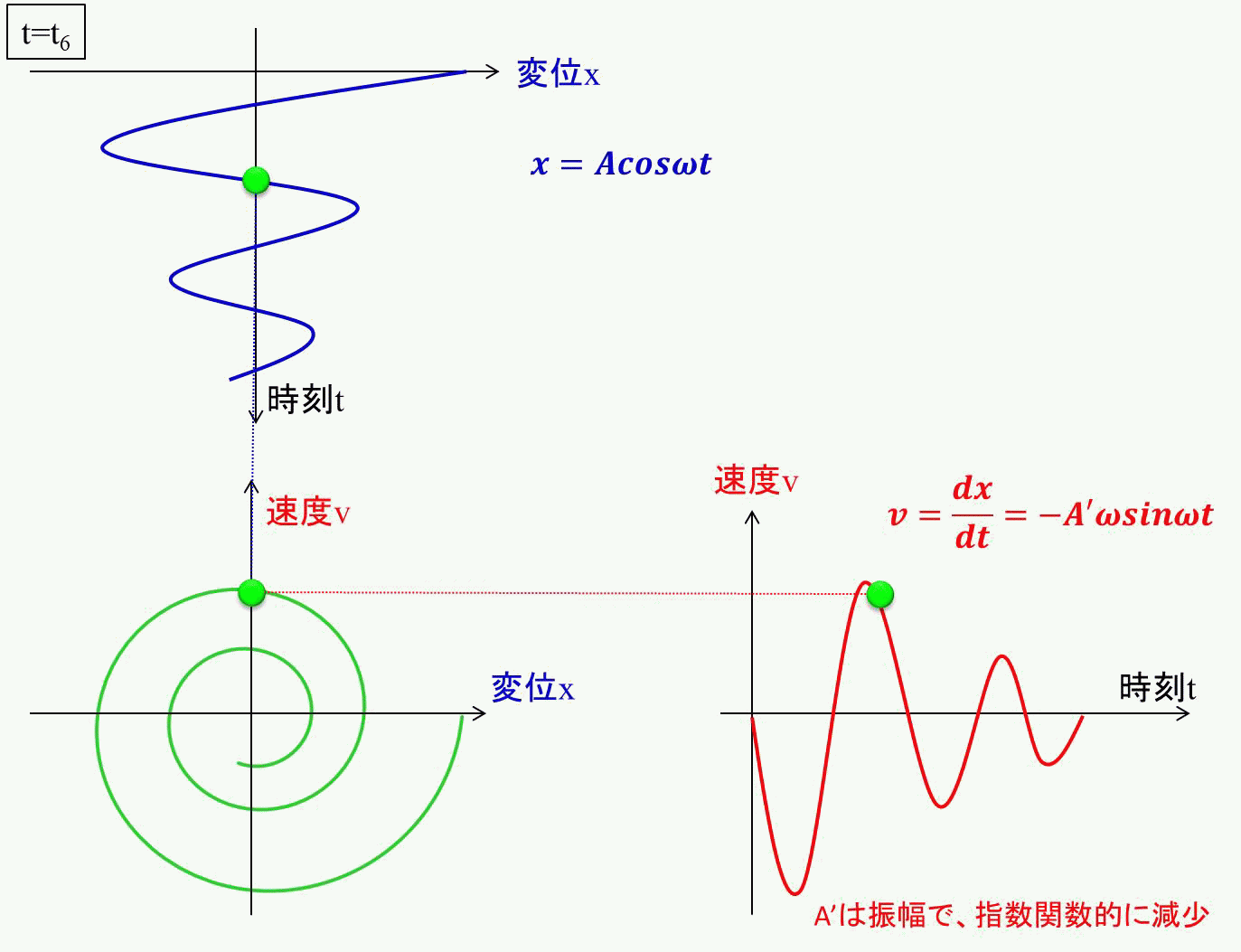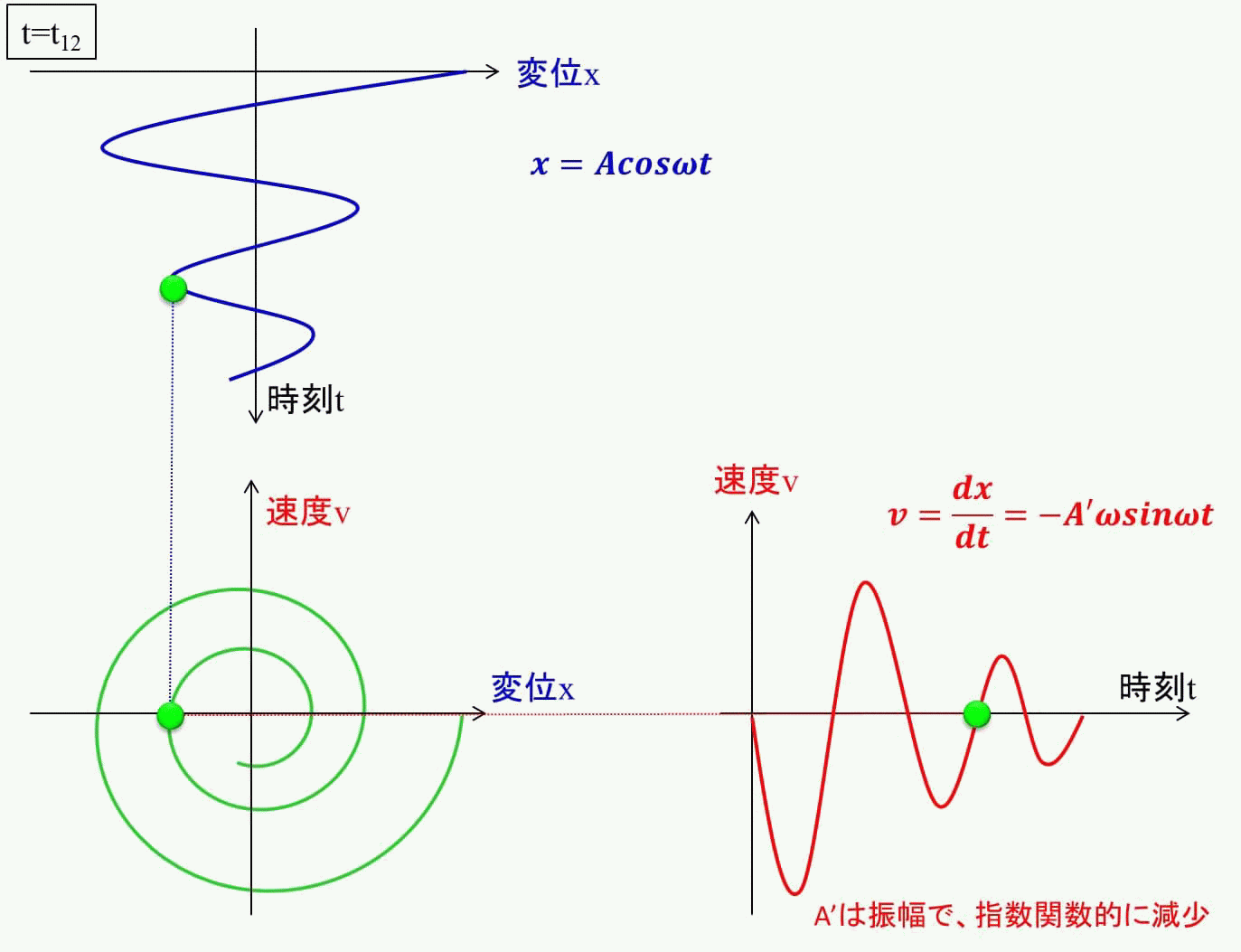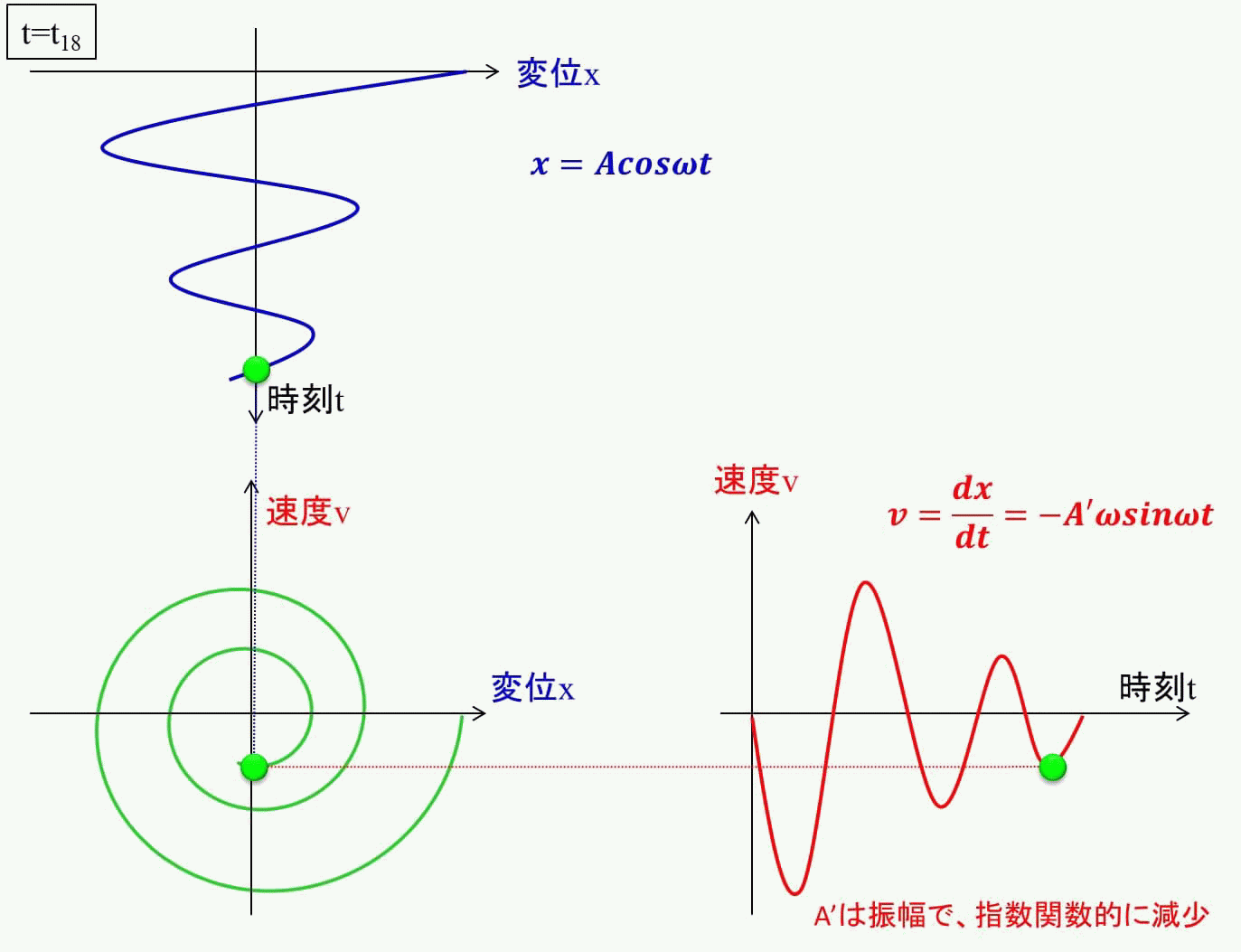
アニメーションで見るとイメージが付きやすいのではないでしょうか?
相平面上をうずまき状に動くことが分かりますね。
まとめ
本記事では減衰振動の場合の相平面について解説しました。
減衰振動の場合、相平面はうずまき状になることを理解していただけたと思います。
導出には等傾線法とグラフからイメージする方法とを解説しました。
どちらも重要ですので、しっかり理解しましょう。
参考文献
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 非線形力学(共立物理学講座6):戸田盛和、渡辺慎介、共立出版株式会社
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。