機械設計しているときに、『共振に気をつけろ』って言われたんですけど、どういうこと??


共振っていうのは、特定の周波数で振動したときに、大きな振動になってしまうことだよ。これが原因でモノが壊れたりするんだ。
本記事では、強制振動と共振について解説します。
イメージをつかんで頂くことをモットーに解説しますので、できるだけわかりやすく説明しますね。
本記事をおススメする人
- 共振現象についてイメージがつかめていない人
- 強制振動の運動方程式を解きたい人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
共振とは
共振:特定の周波数の振動で、大きな振動をする現象
構造物や機械など、形あるものすべてに共振というものは起こります。
このモノが共振する周波数を共振周波数、あるいは固有振動数といいます。
たとえば、橋などの構造物でも共振周波数があり、この周波数で振動を与えると、橋がめちゃくちゃ揺れます。
共振周波数とおなじ周波数の風が橋にあたって、橋を共振させ、壊してしまう、というとんでもないことが現実でも起こっています。
(タコマナローズ橋が良く例として出されます)
ひぇ~・・・恐ろしい・・・


そう、だから構造物を設計するときには、風などの外力の周波数からできるだけ共振周波数を離れさせたり、共振を抑える仕組みが必要があるんだよ。
共振周波数は何で決まる?
共振周波数をできるだけ離すっていうけど、どうするの?


固有振動数は基本的には、モノの形状と材質で決まるので、入力の振動の周波数と異なるようにモノを作っていくよ。
共振周波数のイメージ = 硬いモノは共振周波数が高い
式的に見てみましょう。
強制振動の運動方程式(減衰無し)
まずは外力が働いていない場合、バネにつながれたモデルの単振動の式です。
下記のようになりますね。
$$m\ddot{x}=-kx$$
この式については過去の記事で解説していますので、参考にしてください。
単振動については動画でも解説していますので参考にしてください。
この単振動の運動方程式に強制振動を加えます。
外から周期的な力、\(Fcosωt\)というものを付け加えます。
これを両辺\(m\)で割って整理します。
この微分方程式を解く必要があります。
斉次方程式の一般解と、非斉次方程式の特解で、表されるので、非斉次方程式の一般解は下記となりますね。
詳細の計算は別記事で解説していますのでこちらを参考にしてください。
参考記事
動画でも解説していますので参考にしてください。
強制振動の運動方程式の一般解を\(x(0)=0、\dot{x}(0)=0、ω=ω_0\)として、式を整理すると
となります。
この式を見てみると、振幅部分が\(ft\)となっていますので、時間が経てば経つほど、振幅が大きくなることを示しています。
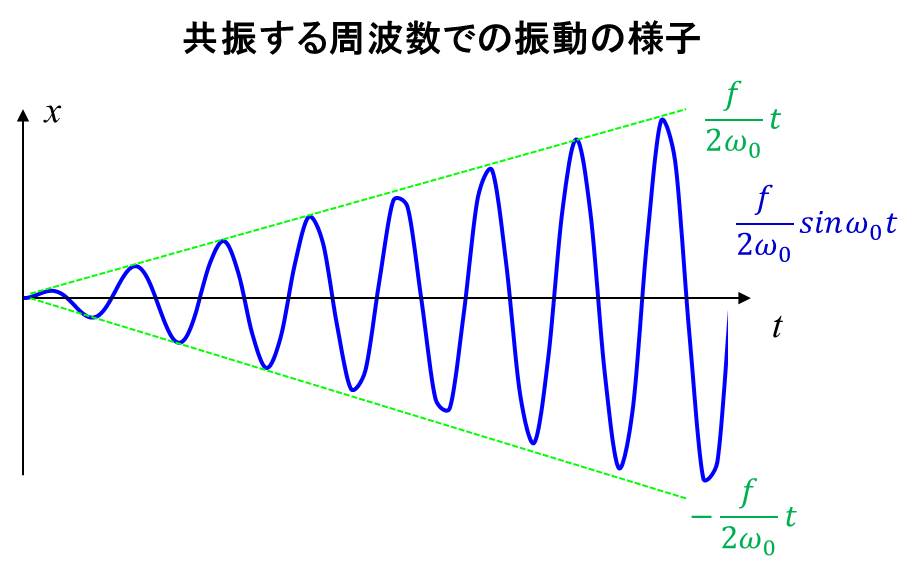
時間を無限大にしてしまうと、振幅も無限大、つまり、とてつもなく大きな振動に発達する、ということです。
これが共振現象です。
共振を抑えるには?
共振したときの振幅を抑える方法ってあるの?


振動を減衰させるようなものをいれてあげれば、共振の振幅を抑えれるよ。
強制振動の運動方程式(減衰あり)
減衰を考慮した振動の運動方程式は、下記の記事で解説しました。
参考記事
減衰振動についても動画でも解説していますので下記を参考にしてください。
下記のような物体がバネとダンパーに繋がれたモデルを考えます。
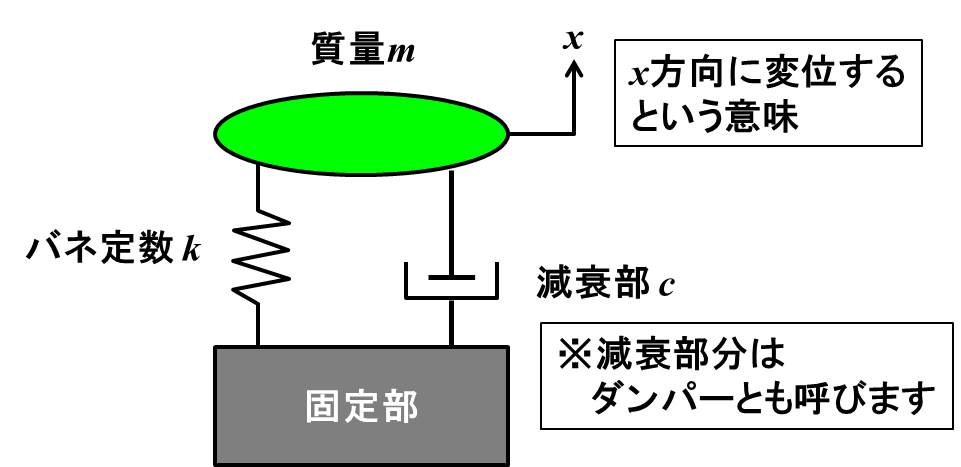
運動方程式は質量を\(m\)、減衰定数を\(c\)、バネ定数を\(k\)とすると、下記のようになります。
この運動方程式は、外力が働いていない自由振動の式ですので、
周期的な外力\(Fcosωt\)を付け加えます。
式を整理します。両辺\(m\)で割り、\(ζ、ω_0、f\)を使います。
で、微分方程式を解くわけですが、長くなるので、詳細の計算は下記の記事を参考にしてください。
参考記事
なお、動画でも解説していますので参考にしてください。
運動方程式を解いて、\(A\)を振幅、δを位相差として、\(x(t)=Asin(ωt-δ)\)の形で表すと、
ここで振幅\(A\)は\(sin\)の係数となるので、
となります。最大値を\(A_{max}\)とすると、\(ω=ω_0\)の時に最大、つまり、外力の周波数とモノの固有振動数が一致したときに最大になりますね。
このときの\(A_{max}\)は、
振幅\(A\)と振動数\(ω\)の関係をグラフに書くと下記になります。
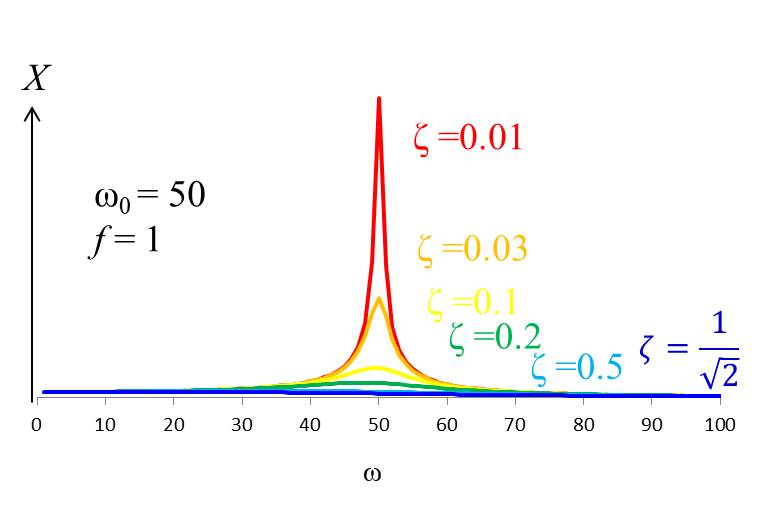
簡単のために\(ω_0=50, f = 1\)で計算しています。
ピークの部分が\(A_{max}\)ですね。
減衰比ζが小さくなると、ピークが鋭くなることが分かりますね。
共振の大きさを示す値 Q値
振動に関わる仕事をしている方は、共振を表現するにあたって、Q値というものが必ずでてきます。
Q値とは、共振ピークがどれだけ鋭くなるか、について示したものです。
共振を抑えるには減衰が効くということを示したましたが、Q値は減衰とふか~く関係しています。
イメージとしては下記のような感じです。
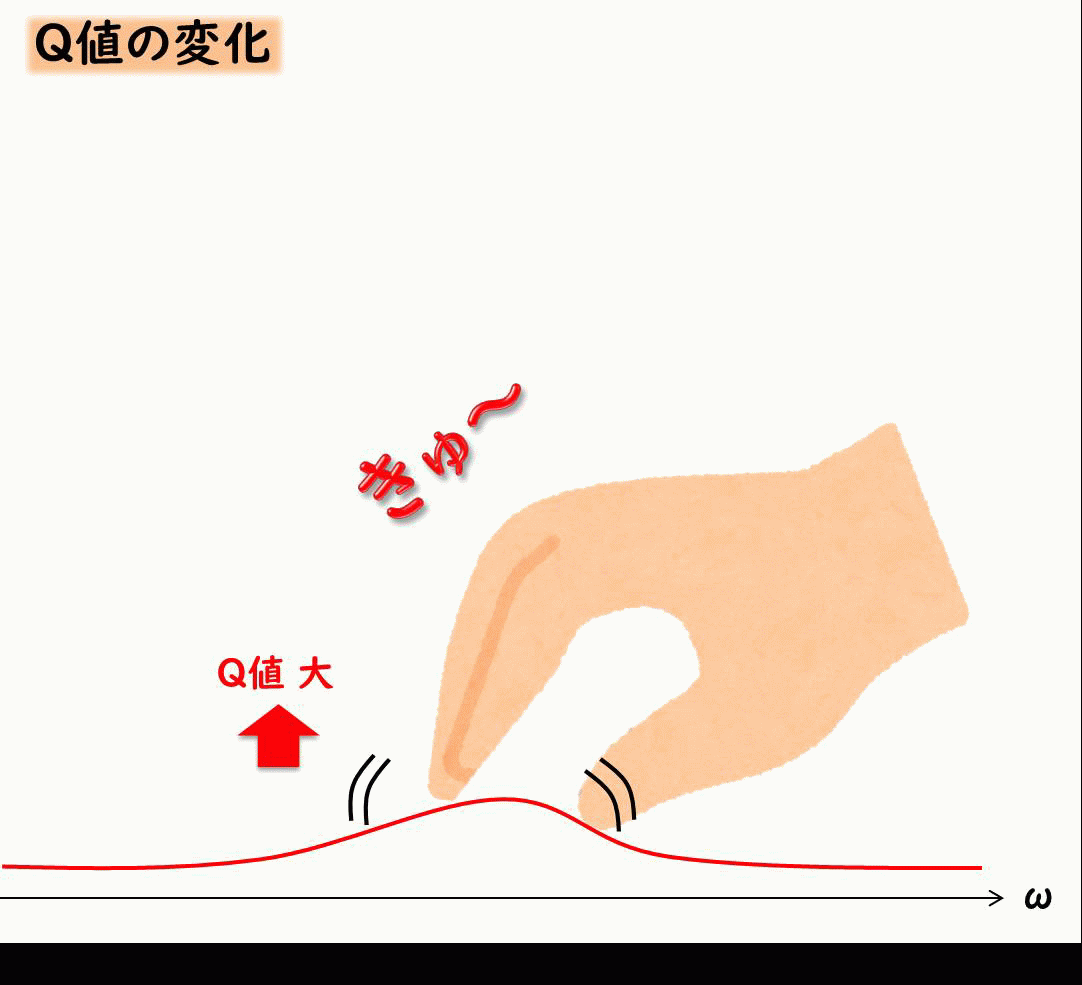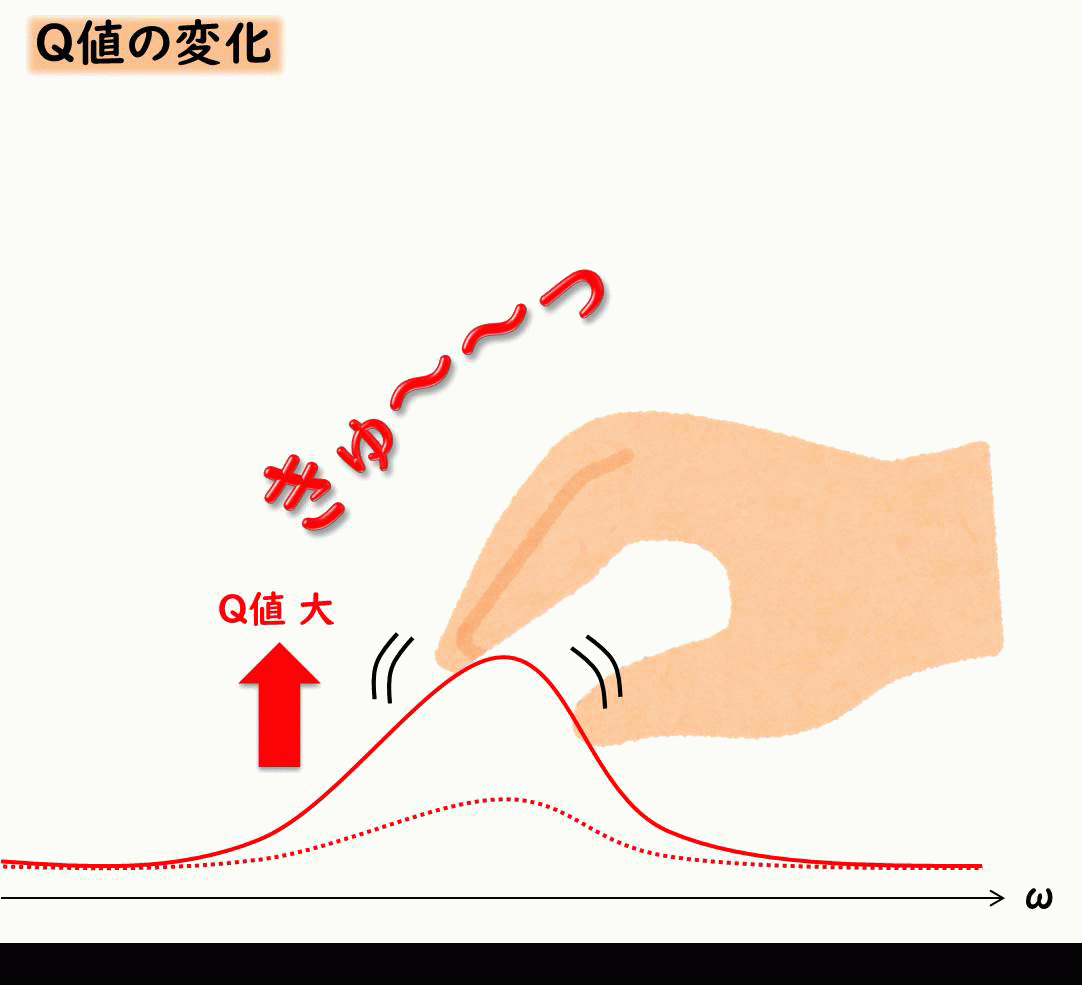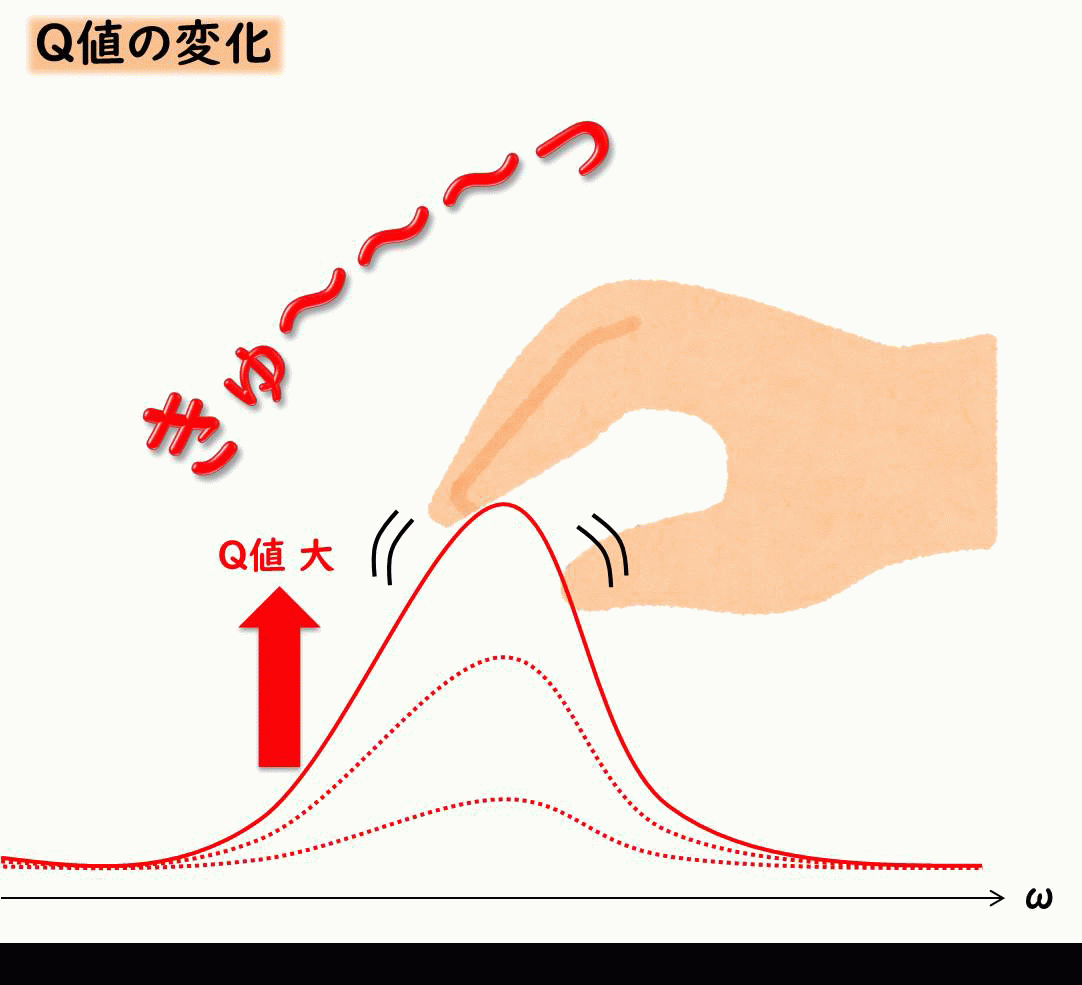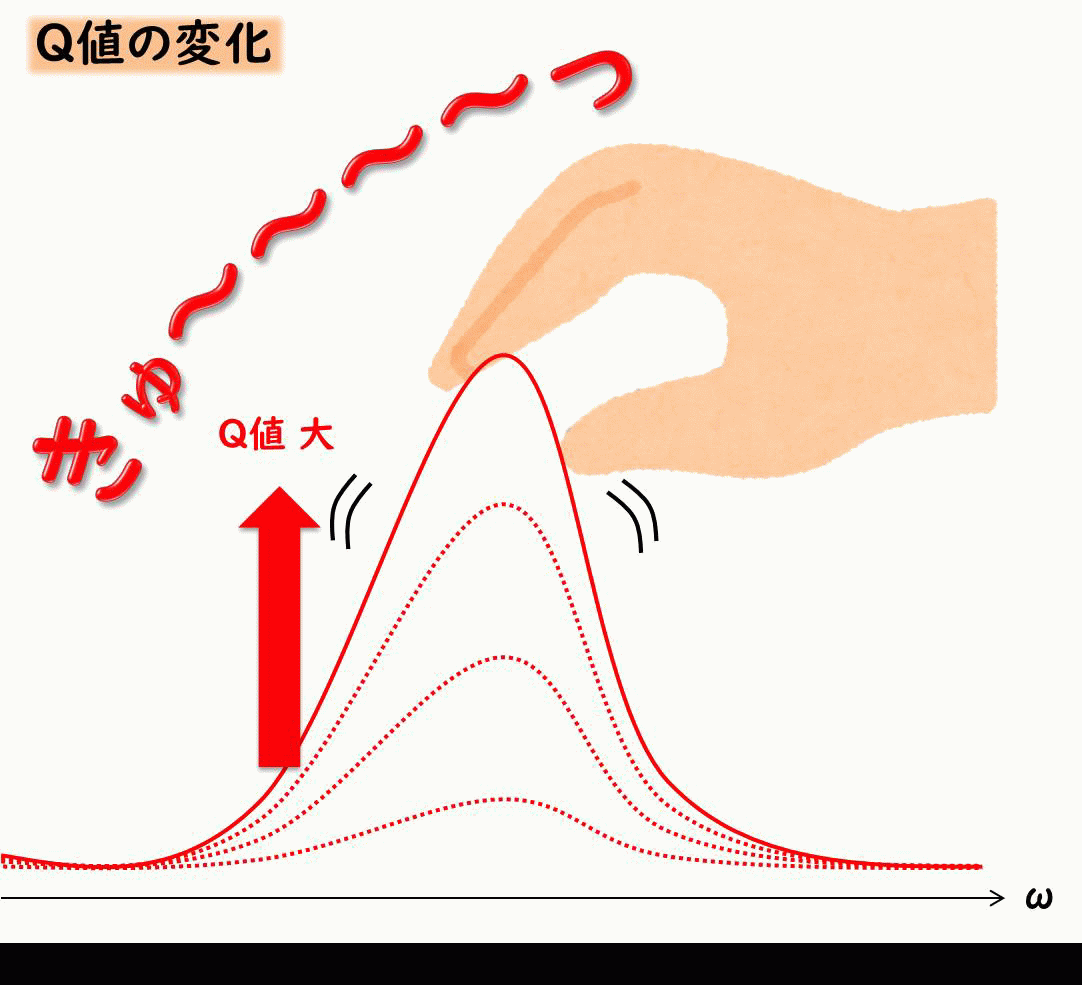
Q値は減衰比ζが小さい場合、
となります。
Q値の導出の詳細については下の記事を参考にしてください。
共振の大きさQ値を抑えるには、減衰比ζを大きくすればよいわけですね。
まとめ
本日は強制振動の共振について解説しました。
減衰がある場合と無い場合で、共振ピークが無限大になるかどうかが決まります。
また、減衰させればさせるほど、共振ピークの大きさは小さくなり、ピークの鋭さをQ値という値で表現することを解説しました。
共振現象は力学やら電磁気学やらいろんな分野で出没する現象です。
本記事で解説した共振のイメージを身に付けて、今後の勉強、仕事に役立てていただければ幸いです。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の複素解法③減衰ありの強制振動の運動方程式
