ねじりの変形が苦手なんだけど…イメージがつかなくって…


じゃあ今日はねじり応力について詳しく解説するね。
本日は『ねじり』について解説します。
押さえる点をしっかりと押さえておけば理解できるようになりますので、図をみてしっかりとイメージできるようになりましょう。
せん断応力との関係性を重点的に解説しますので、せん断応力が苦手な方は過去の記事を参考にしていただければと思います。
動画でも解説していますので、是非参考にしていただければと思います。
ねじりを発生させる力と応力
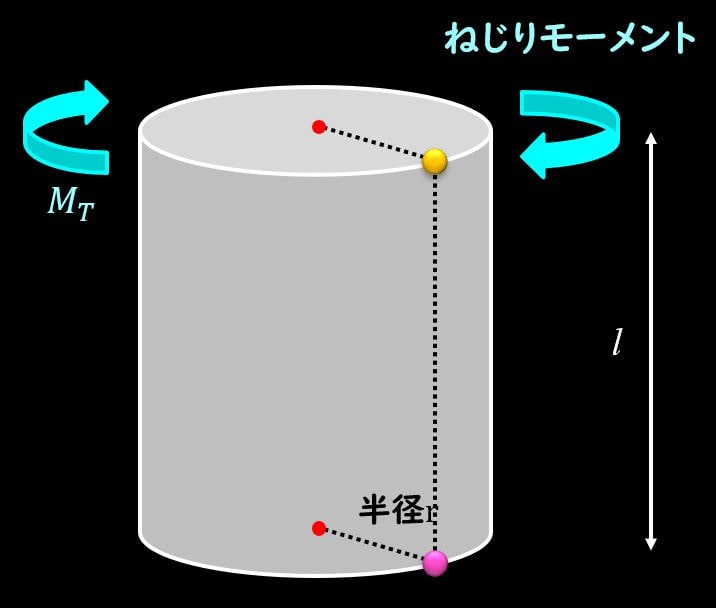
まずねじりを発生させる力についてですが、上図のように、丸棒にねじれの力を加えましょう。
この加えた力をねじれモーメントと呼んだり、トルクと呼んだりします。
このねじれモーメントによって発生する内力、すなわちねじれ応力がどのようになっているかというと、下図です。
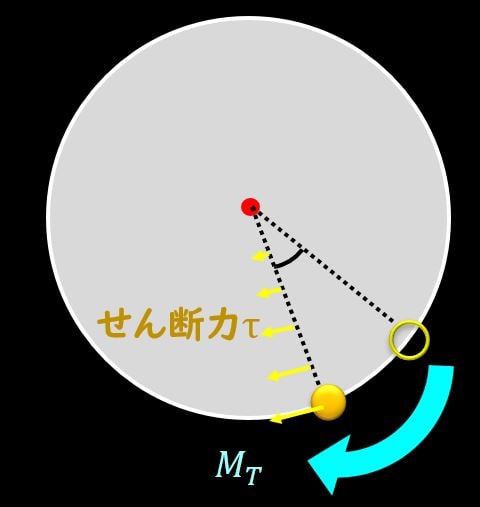
このように丸棒の断面を見ていただくと、中心からの距離が大きくなると、応力も大きくなります。
この応力は、中心を境に逆方向に働く応力となるので、せん断応力となります。
ねじれ応力はせん断応力であり、円周上で最大となることをしっかりと押さえておきましょう。
ねじれ角と比ねじれ角(ねじれ率)
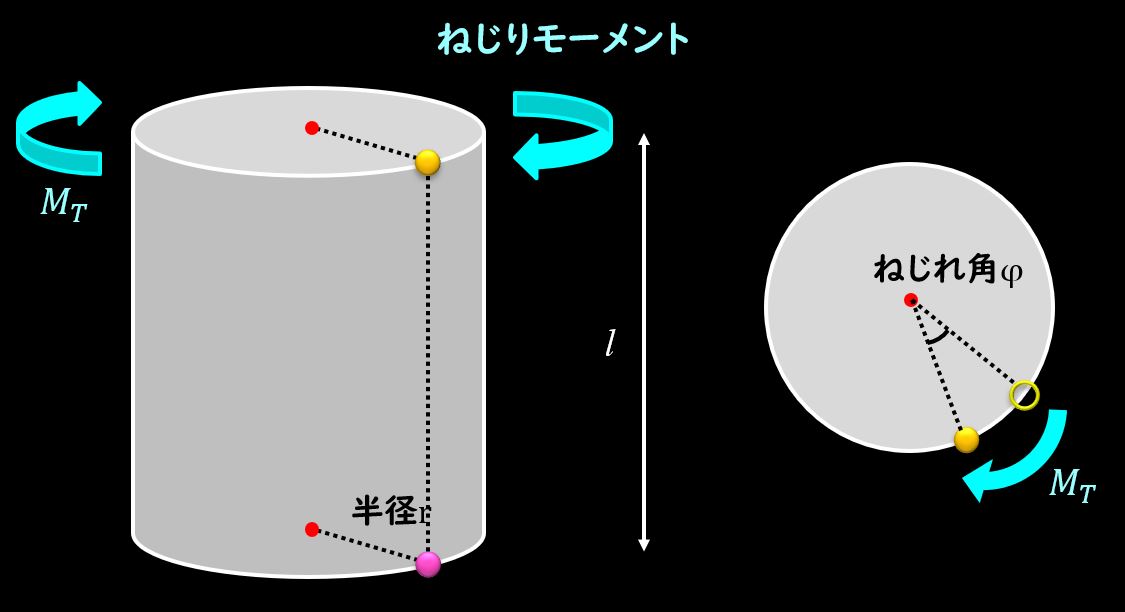
さて、このねじれ角がイメージつきにくいと思いますので、図を用いて解説します。
ねじれ角は上図の\(φ\)で表された部分になります。
比ねじれ角は単位長さあたりのねじれ角をあらわし、図の丸棒の単位長さの部分を切り出して考えます。
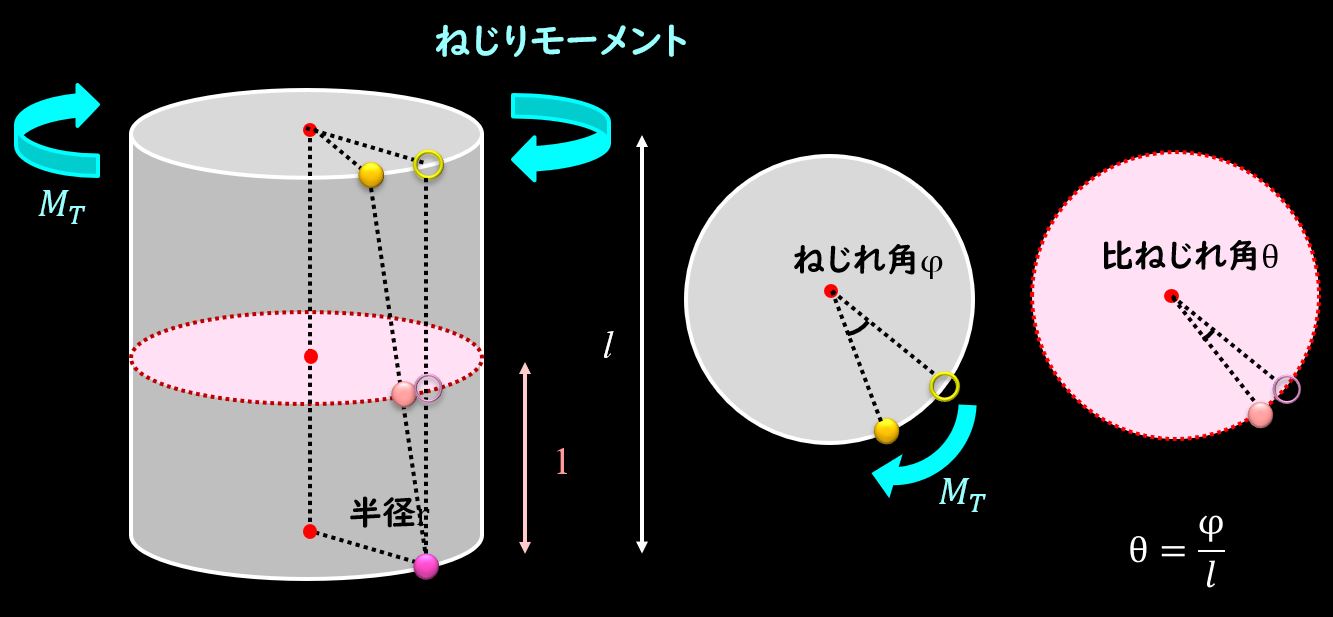
上図のように、長さが1の部分を取り出し、この領域でのねじれ角\(θ\)を比ねじれ角と呼んでいます。
この比ねじれ角は、ねじれ角\(φ\)と丸棒の長さ\(l\)を用いて下記のように表すことができます。
$$θ=\frac{φ}{l}$$
せん断応力とのひもづけ
さて、ねじれによって発生したせん断応力がどのように定式化されるかを考えてみましょう。
単位長さあたりの丸棒を下図のように切り出し、横から見ます。
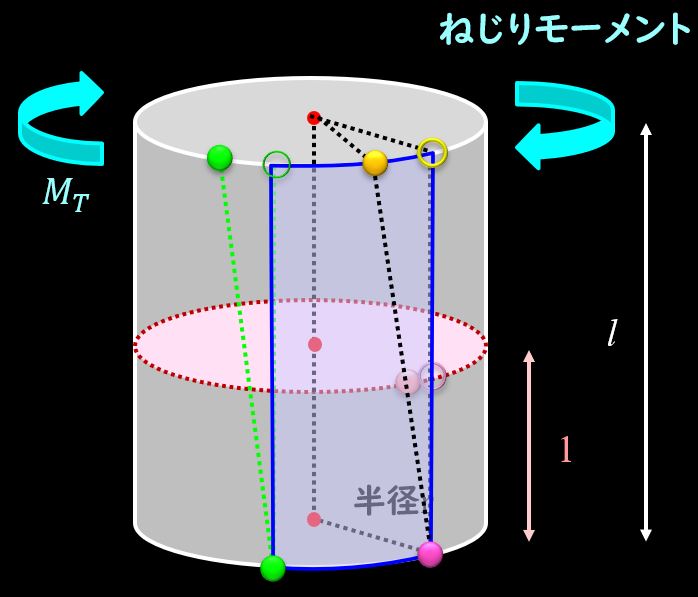
この状態でねじれを発生させましょう。
すると、長方形から平行四辺形に変形したように見えますね。
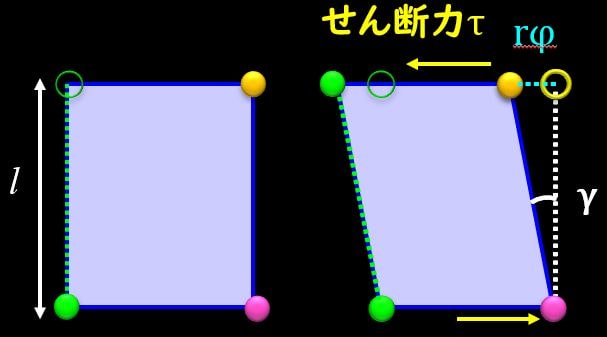
このときのひずみを\(γ\)とすると、
$$γ=\frac{rθ}{1}=rθ$$
と書くことができます。
この\(γ\)がまさにせん断ひずみと同じになっています。
せん断応力は、フックの法則により、横弾性係数とせん断ひずみをかけることで表すことができて、
$$τ=Gγ=Grθ$$
となります。
このせん断応力に半径\(r\)が含まれていることに注目していただきたいのですが、\(r\)に比例してせん断応力が大きくなることになります。
棒材を上面から見ると、\(r\)に比例するので、下図のように円周上で最大となります。
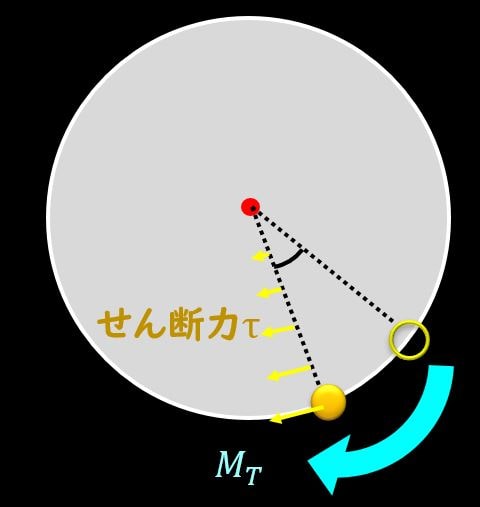
ねじれによって発生したせん断応力分布は中心でゼロ、円周上で最大となるわけですね。
まとめ
ねじれの応力について解説しました。
ねじれ応力とせん断応力は密接に関係しており、今回取り扱ったような丸棒材の上面から見ると、円周上で最大となります。
ねじれ応力の分布をかならず覚えておくようにしましょう。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
次の記事 → 材料力学 初心者向け-曲げ応力・応力度についてわかりやすく解説
