曲げモーメントってよくわからないんだけど…


今日は曲げの基礎とも言える曲げモーメントについて解説するね。
今回は曲げモーメントについて解説します。
曲げモーメントは『 荷重によって梁を曲げた時に発生するモーメント』です。
この曲げモーメントによって梁が曲がる、と考えていただければと思いますが、
今回はこのイメージがしっかりできるように解説していきたいと思います。
曲げモーメントって?
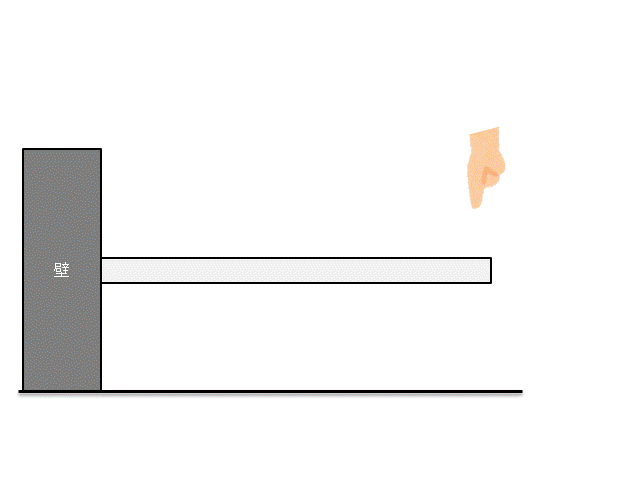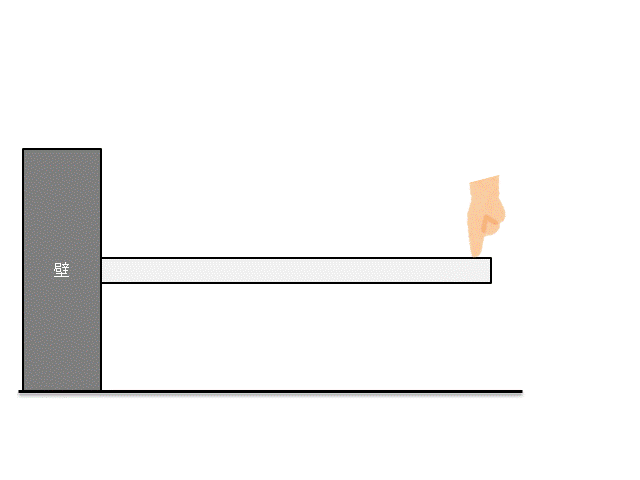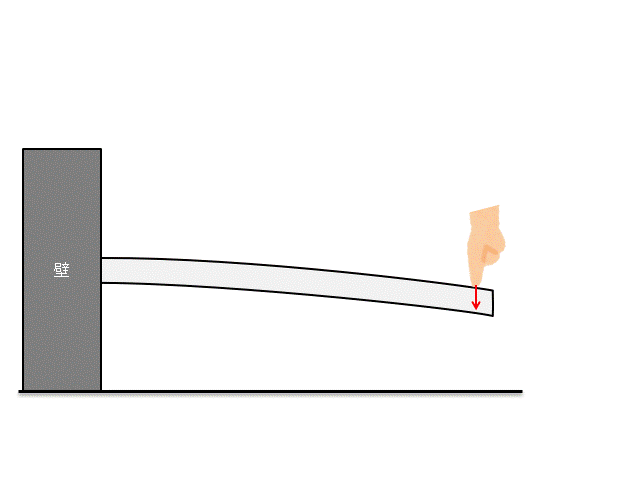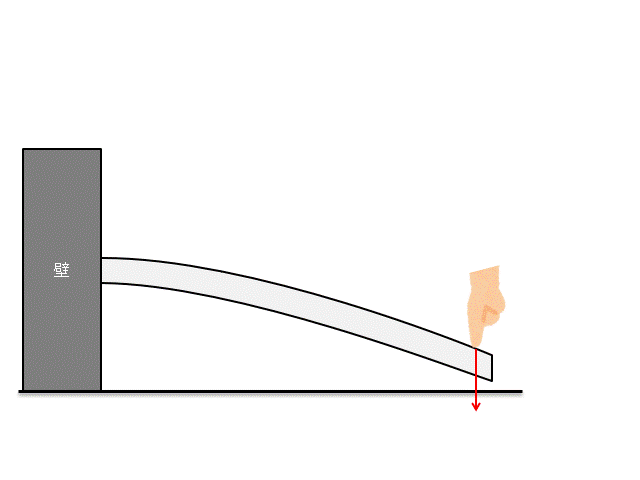
上図のような片持ち梁を考えてみましょう。
この片持ち梁の先端にゆっくりと力を与えて、梁を曲げた状態で静止させましょう。
静止しているので、梁の一部を取り出してみて、力のつりあいを考えてみます。
試しに先端付近を取り出してみると、下図のようになりますね。
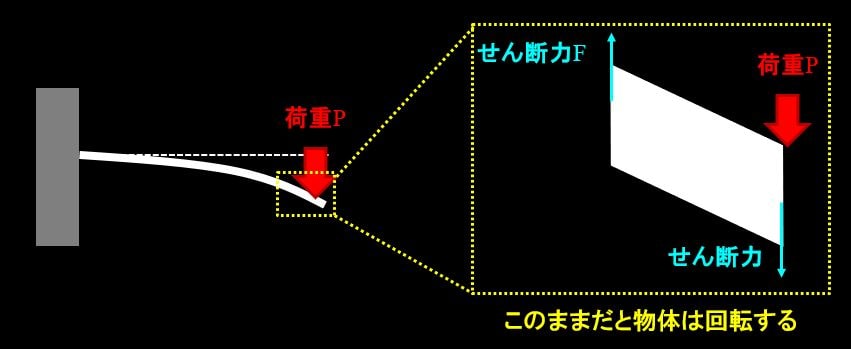
まず、荷重Pが梁の先端に下向きにかかっています。
この力とつりあうように、左端にはせん断力\(F\)が上向きに発生し、力のつり合いが保たれます。
さらに、大きさのある物体が静止しているので、力のつり合いに加えて、モーメントのつり合いも考える必要があります。
モーメントは物体を回転させるものでしたね。
取り出している領域の長さを\(L\)とすると、荷重\(P\)をかけることによって発生する力のモーメントは
$$P×L$$
と表すことができます。
現在、この梁は静止しているので、この大きさとつりあうようなモーメントが発生しないと、梁が回転してしまいます。
この荷重\(P\)とつりあうようなモーメントが曲げモーメントとなります。
よって曲げモーメントMは
$$M=P×L$$
と書くことができます。
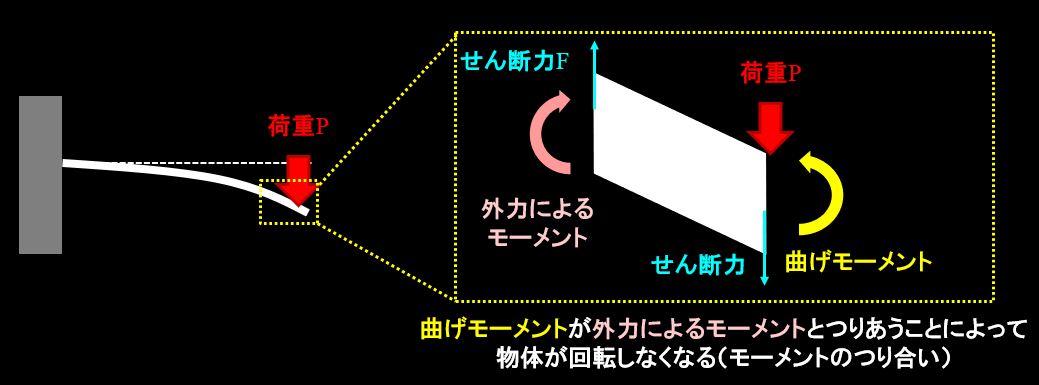
また、曲げモーメントには向きによって符号があります。
上向きに曲げようとするモーメントがプラス、下向きに曲げようとするモーメントがマイナスです。
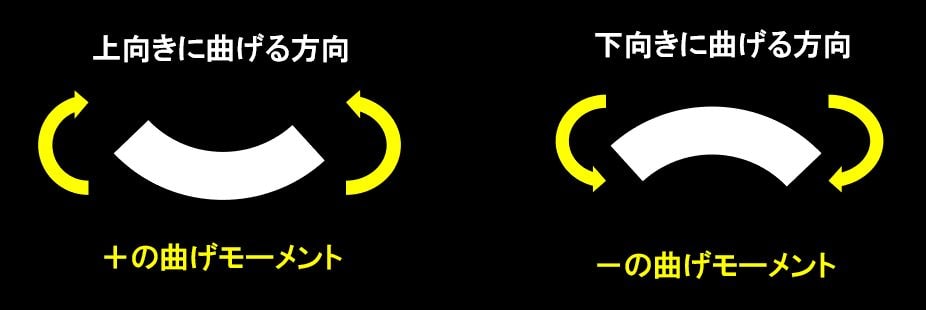
今回は下向きに曲げようとしているので、曲げモーメントはマイナスです。
※ただし、教科書などによっては符号を逆に定義している場合もありますので、ご注意ください。
BMDについて
あれ?じゃあ曲げモーメントって、梁の場所によって変わるの?


その通りだよ。曲げモーメントの分布を図にしたものをBMD (Bending Moment Diagram)と呼ぶよ。
ちなみにM図と呼ぶこともあります。
例の片持ち梁の場合は、下記のようなグラフになりますね。
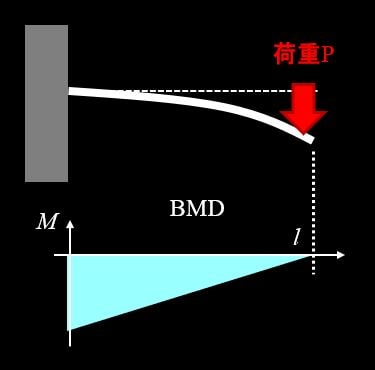
これが初学者みんな大嫌いのBMDですね(笑)
僕は学び始めた頃、さっぱりわからなかったです(汗)
この図で大事なのは、『根本に1番大きな曲げモーメントが発生している』ということです。
つまり、片持ち梁を曲げると、壊れる時は根本から壊れる、ということになります。
梁の支持の仕方や荷重のかけ方によって、BMDは変化しますので、詳細は今後の記事でまとめていきますので、楽しみにしていただければと思います。
まとめ
本記事では曲げモーメントについて解説しました。
曲げモーメントで重要な考え方としては、『外力によるモーメントとつりあうモーメントであること』、でした。しっかりと意味を理解して、BMDまで書けるようにしていきましょう。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
