行列とベクトルの掛け算-1次変換（線形変換）の意味をわかりやすく解説

文字だとわかりにくいので、適当に数字を入れてみましょう。

$$\left(\begin{array}{cc}1&2\\3&4\end{array}\right)\left(\begin{array}{c}1\\2\end{array}\right)$$

この掛け算を計算してみると、

$$\left(\begin{array}{cc}1&2\\3&4\end{array}\right)\left(\begin{array}{c}1\\2\end{array}\right)=\left(\begin{array}{c}5\\11\end{array}\right)$$

このようになります。

ここで、行列Aとベクトル\(a\)、\(b\)を下記のように定義します。

$$A=\left(\begin{array}{cc}1&2\\3&4\end{array}\right)$$

$$\vec{a}=\left(\begin{array}{c}1\\2\end{array}\right)$$

$$\vec{b}=\left(\begin{array}{c}5\\11\end{array}\right)$$

このようにすると、もとの式は下記のように書けます。

$$A\vec{a}=\vec{b}$$

この式を見ると、『ベクトル\(\vec{a}\)は行列Aをかけることによって、ベクトル\(\vec{b}\)に変化した』ということを示していますね。

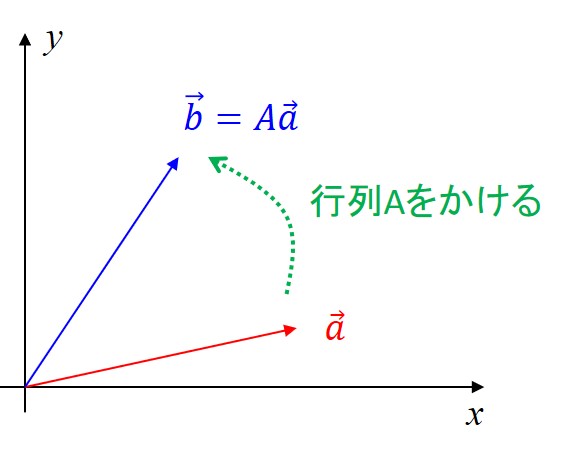
行列にはベクトルを異なるベクトルに変化させる性質がある、 ということを理解しておきましょう。 どういう形に変化させているか まず、一般的な形で解説します。

$$A=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)$$

$$\vec{a}=\left(\begin{array}{c}x\\y\end{array}\right)$$

結論を述べますと、下記になります。

 

行列Aはベクトル\(\vec{a}\)を\(xy\)座標系（直交座標系）から、行列Aの列ベクトルが張る空間へ変化させている

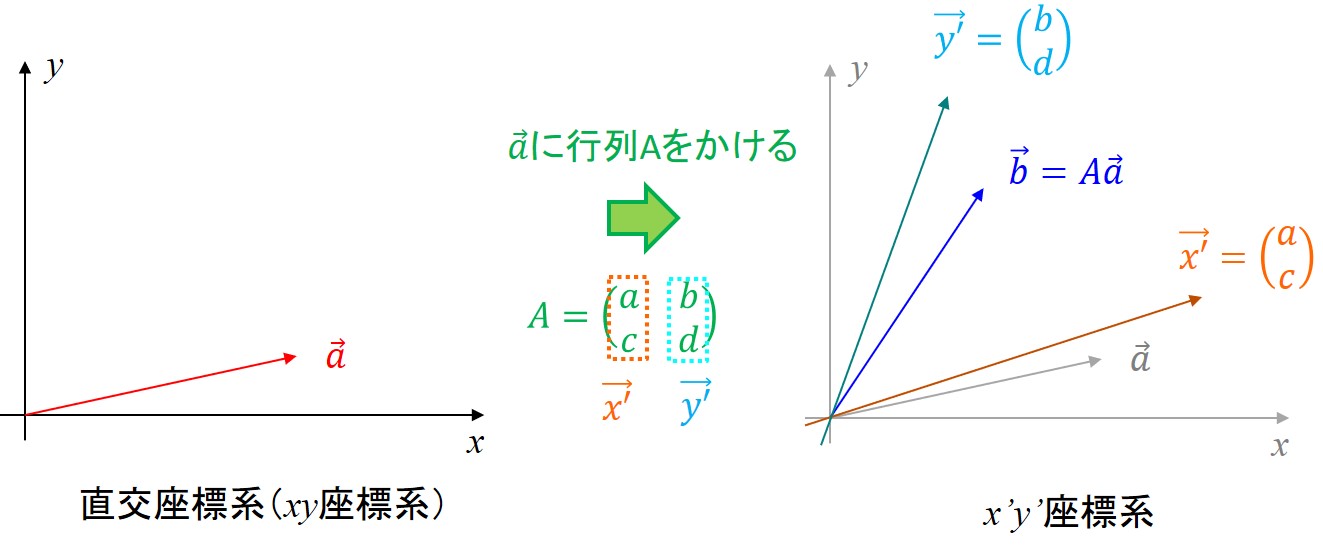
なんのこっちゃ？と思われる方も多いと思いますので、解説していきますね。

行列Aの見方として、上記のように列ベクトルが二つ(\(\vec{x'},\vec{y'}\))並んでいる、という風に見てください。

後々こうなっているとわかりますので、まずはそういうものだと思ってくださいね。

それでは解説に移ります。

行列Aの中にある列ベクトルを\(\vec{x'}\)、\(\vec{y'}\)という風に定義します。

$$\vec{x'}=\left(\begin{array}{c}a\\c\end{array}\right)$$

$$\vec{y'}=\left(\begin{array}{c}b\\d\end{array}\right)$$

まず、ベクトル\(a\)について直交座標系の単位ベクトル\(\vec{e_x}\)、\(\vec{e_y}\)を用いて表すと、

$$\vec{a}=\left(\begin{array}{c}x\\y\end{array}\right)=x\left(\begin{array}{c}1\\0\end{array}\right)+y\left(\begin{array}{c}0\\1\end{array}\right)=x\vec{e_x}+y\vec{e_y}$$

$$\vec{e_x}=\left(\begin{array}{c}1\\0\end{array}\right),\vec{e_y}=\left(\begin{array}{c}0\\1\end{array}\right)$$

となります。

次に、ベクトル\(\vec{a}\)に行列Aをかけると、下記のように計算できます。

$$\begin{eqnarray}\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right) &=&\left(\begin{array}{cc}a&b\\c&d\end{array}\right)(x\vec{e_x}+y\vec{e_y}) \\\\&=&x\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\left(\begin{array}{c}1\\0\end{array}\right) +y\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\left(\begin{array}{c}0\\1\end{array}\right) \\\\&=&x\left(\begin{array}{c}a\\c\end{array}\right)+y\left(\begin{array}{c}b\\d\end{array}\right)\end{eqnarray}$$

このように行列Aをかけることで、基底となる単位ベクトルの部分が変化していることがわかります。

つまり、座標軸が\(xy\)座標から、行列の列ベクトルによって示される座標系に変化したわけですね。

行列は列ベクトルで見ることが大事なわけです。

$$\begin{eqnarray}\left(\begin{array}{cc}1&2\\3&4\end{array}\right)\left(\begin{array}{c}1\\2\end{array}\right) &=&\left(\begin{array}{c}5\\11\end{array}\right)\end{eqnarray}$$

この行列とベクトルの掛け算の計算はこのようになります。

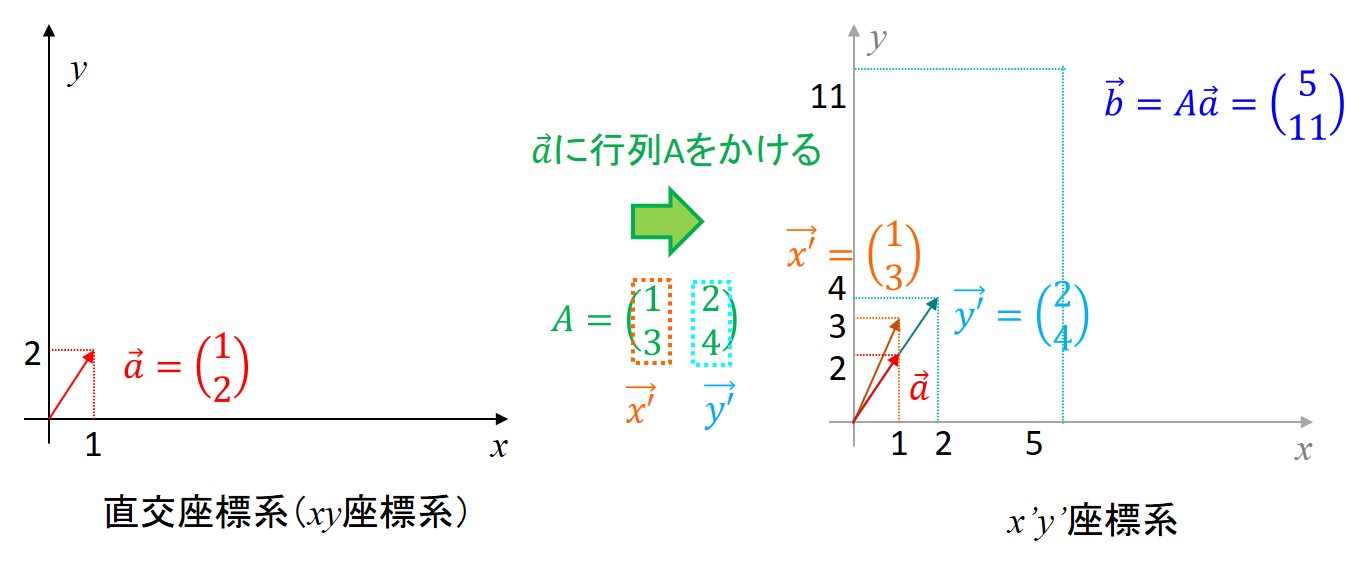
先ほど行った計算結果のように、行列Aの列ベクトルを単位ベクトルとして書き直すと、下記のようになります。

$$\begin{eqnarray}\left(\begin{array}{c}5\\11\end{array}\right) =1\left(\begin{array}{c}1\\3\end{array}\right)+2\left(\begin{array}{c}2\\4\end{array}\right)\end{eqnarray}$$

このように書けるのですが、グラフで示した方がイメージがつきやすいと思いますので、グラフを見てみましょう。

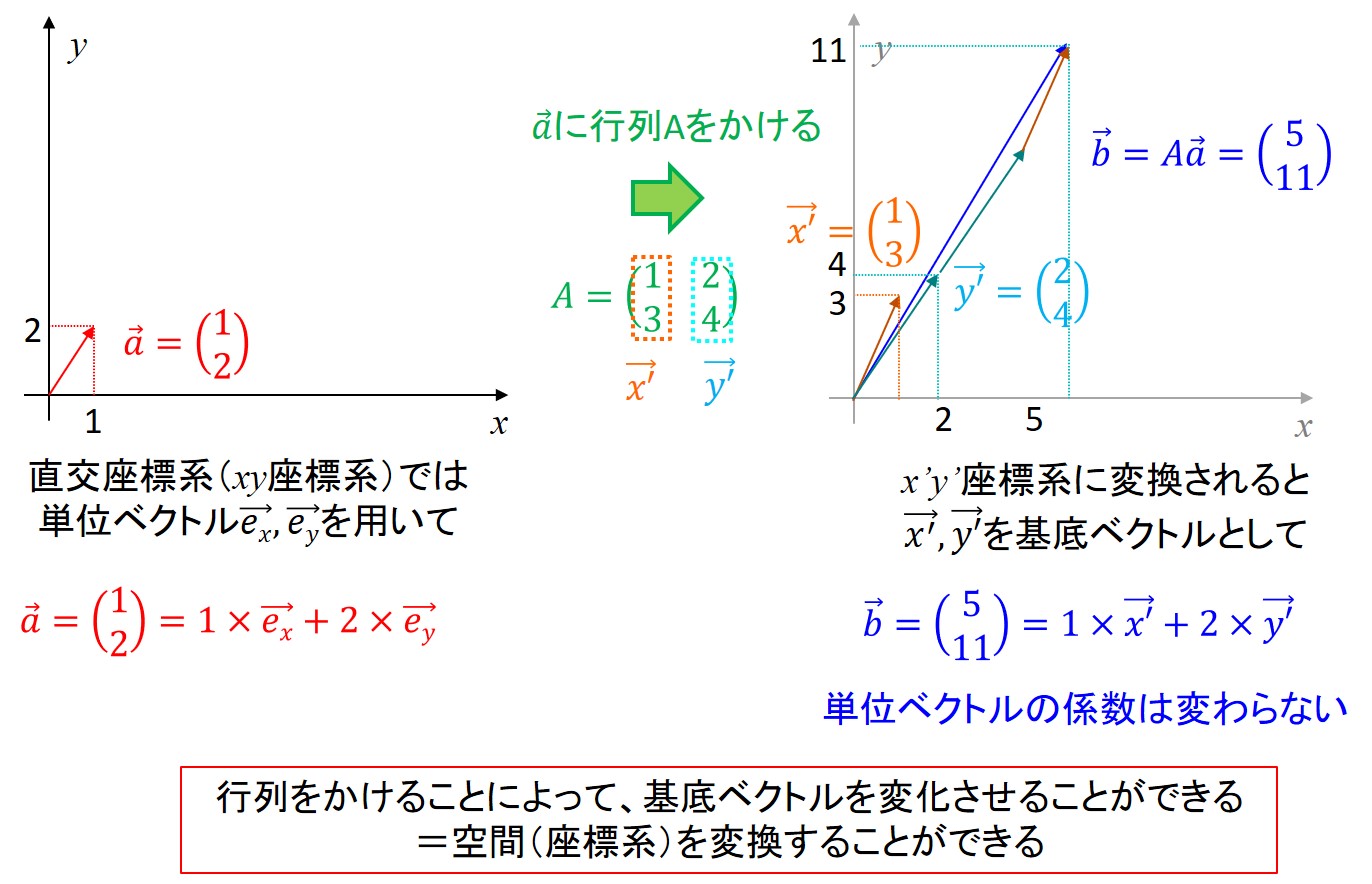
直交座標から行列の列ベクトルで示される座標系に変換されていることがわかりますね。

私的なイメージですが、行列によって空間を捻じ曲げている感じです。

今回は行列×ベクトルのイメージがわかるように解説しました。 このイメージが非常に大事ですので、自分でも1度は計算しながら理解して頂ければと思います。