同次微分方程式とか非同次微分方程式とか区別がよくわからないんだけど


同次方程式や非同次方程式は微分方程式の分野でもよく使うから、区別できるように解説するね。
本日は同次微分方程式と非同次微分方程式について解説します。
ちなみに斉次方程式や非斉次方程式と呼んだりもします。
前回の記事で微分方程式の名前の付け方を解説したときに、同次、非同次について簡単に解説していますので、そちらも参考にしていただければと思います。
物理の分野では当たり前のようにこれらを使い分けて、解はこのようになる、 という説明がされてチンプンカンプンになった人もいらっしゃると思います。
今回は、同次方程式と非同次方程式の違いについてと、非同次微分方程式の解が同次微分方程式の一般解と非同次微分方程式の特殊解の和で表されることを示します。
初学者でもわかるように解説しますので、しっかり理解しておきましょう。
同次方程式と非同次方程式の違い
微分に関する項を左辺に持ってきたとき、右辺がゼロかどうかで同次か非同次かが決まります。
- 右辺がゼロ→同次方程式
- 右辺がゼロでない→非同次方程式
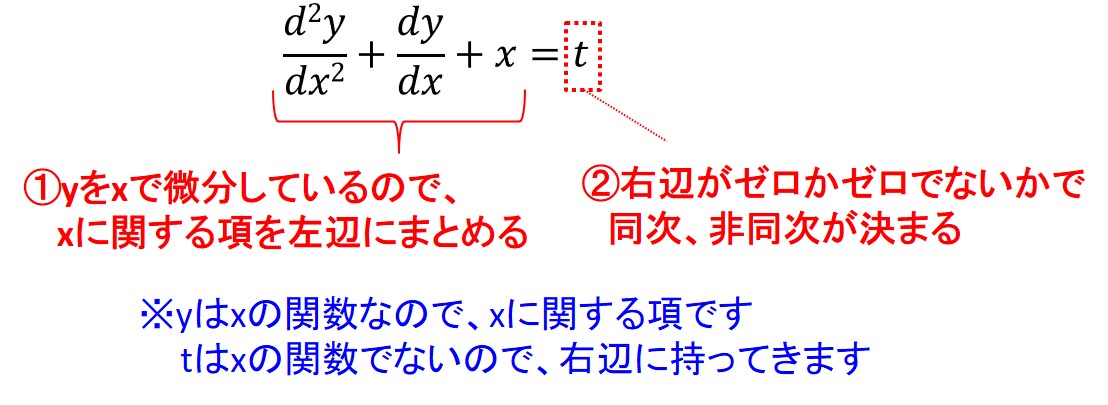
具体例
例を見てみましょう。
$$\frac{dy}{dx}=0$$
これは右辺がゼロなので同次方程式です。
$$\frac{d^2y}{dx^2}=a$$
これは右辺にaが残っていますので、非同次方程式となります。
では下の式はどうでしょう?
$$\frac{dx}{dt}=x$$
答えは同次方程式です。
これは\(x\)についての微分方程式なので、右辺の\(x\)を左辺に持ってくる必要があります。
$$\frac{dx}{dt}-x=0$$
これなら同次方程式とわかるのではないでしょうか?
微分に関する項を左辺に持ってきたとき、右辺がゼロかどうかで同次か非同次かが決まりますので、 この微分方程式は\(x\)について左辺に持ってくる必要があるわけです。
同次微分方程式と非同次微分方程式の解の関係
下記のような同次線形微分方程式を考えます。
$$\frac{dx}{dt}+x=0$$
この同次線形微分方程式の一般解をx=αとすると、
$$\frac{dα}{dt}+α=0$$
となります。
ここで同じ同次微分方程式の右辺にAという定数を与えて、非同次微分方程式にしてみます。 $$\frac{dx}{dt}+x=A$$
この非同次微分方程式の特殊解をβとすると
$$\frac{dβ}{dt}+β=A$$
\(\frac{dx}{dt}+x=A\)と上式の差を取ると、
$$\frac{d(x-β)}{dt}+x-β=0$$
\(X=x-β\)とすると、
$$\frac{dX}{dt}+X=0$$
と書けます。
これは元の同次方程式で$x$を$X$に書き換えただけですので、一般解は
$$X=α$$
となります。$X=x-β$なので、元の非同次微分方程式の一般解は、
$$x=α+β$$
このように、非同次微分方程式の解は、同次方程式の一般解αと非同次微分方程式の特殊解βの和で表すことができます。
これが非常に重要で、大抵の微分方程式の授業では、 同次方程式の一般解を求めて、非同次微分方程式は特殊解だけもとめて足してあげる、ということをしているわけですね。
まとめ
同次方程式と非同次方程式の違いについて解説しました。
左辺に微分に関する項をまとめたとき、右辺がゼロであれば同次方程式、 ゼロでなければ非同次方程式となります。
また、非同次微分方程式の一般解は、同次微分方程式の一般解と非同次微分方程式の特殊解の和となることをしっかりと覚えておきましょう。
微分方程式の初心者向けのおススメ教科書・参考書はこちら
