微分方程式を解くために、結局ラプラス変換するってなると、積分しないといけないんだったら面倒だよ


毎回ラプラス変換で積分すると時間がかかるから、ラプラス変換表を使うといいよ。
今回はラプラス変換で積分が面倒な人に向けて、ラプラス変換表について解説します。
私もラプラス変換を手計算で毎回やるのはしんどいですよ・・・
変換表といっても、メジャーなラプラス変換について結果をまとめた表です。
よく使うラプラス変換は暗記してしまえばよいですし、複雑なものは変換表を使って対応しましょう。
また、重要な関数については、筆者が計算したノートの画像を張り付けていますので、そちらで導出を確認してください。
そもそもラプラス変換って何?という人は、下記の過去記事を参考にしてください。
ポイント
- ラプラス変換について理解したけど、使い方がよくわからない人
- ラプラス変換表を知りたい人
- 重要な関数のラプラス変換の導出を知りたい人
ラプラス変換表
よく使う関数のラプラス変換を一覧にしたものをラプラス変換表と呼びます。
いろんなサイトにラプラス変換表がありますが、私がまとめたものを示しますね。
tのn乗の関数、δ関数など
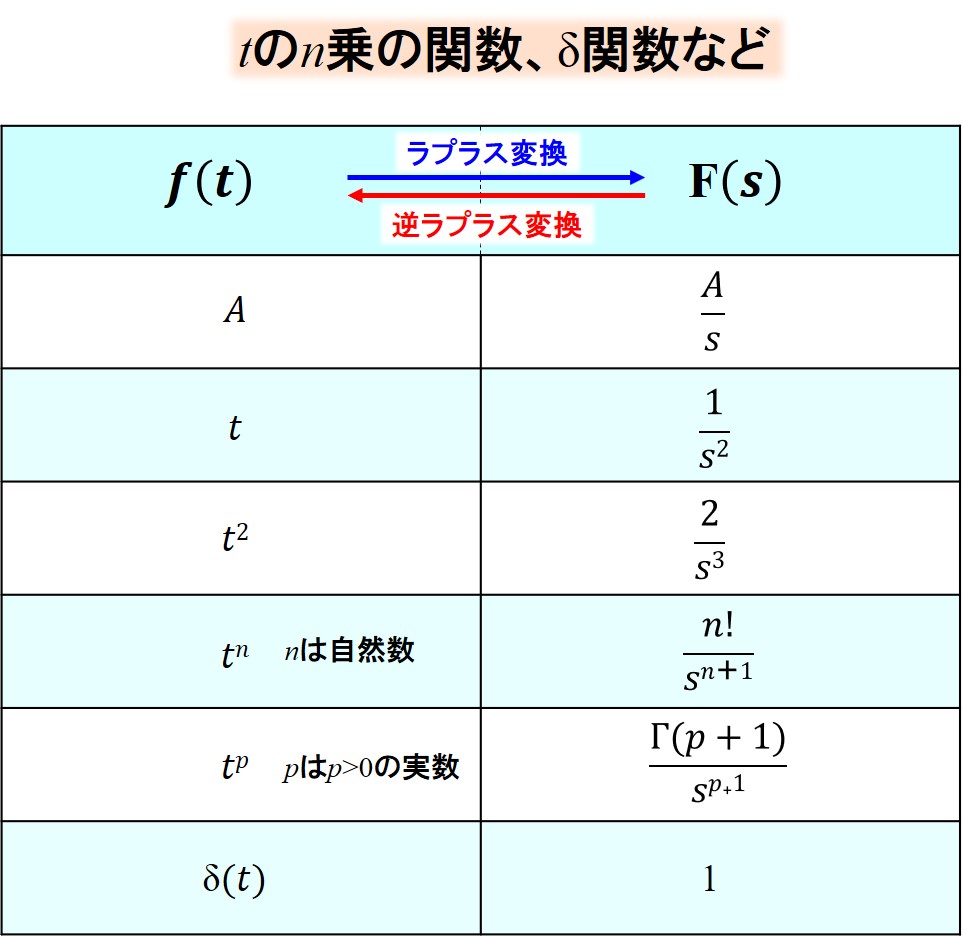
三角関数
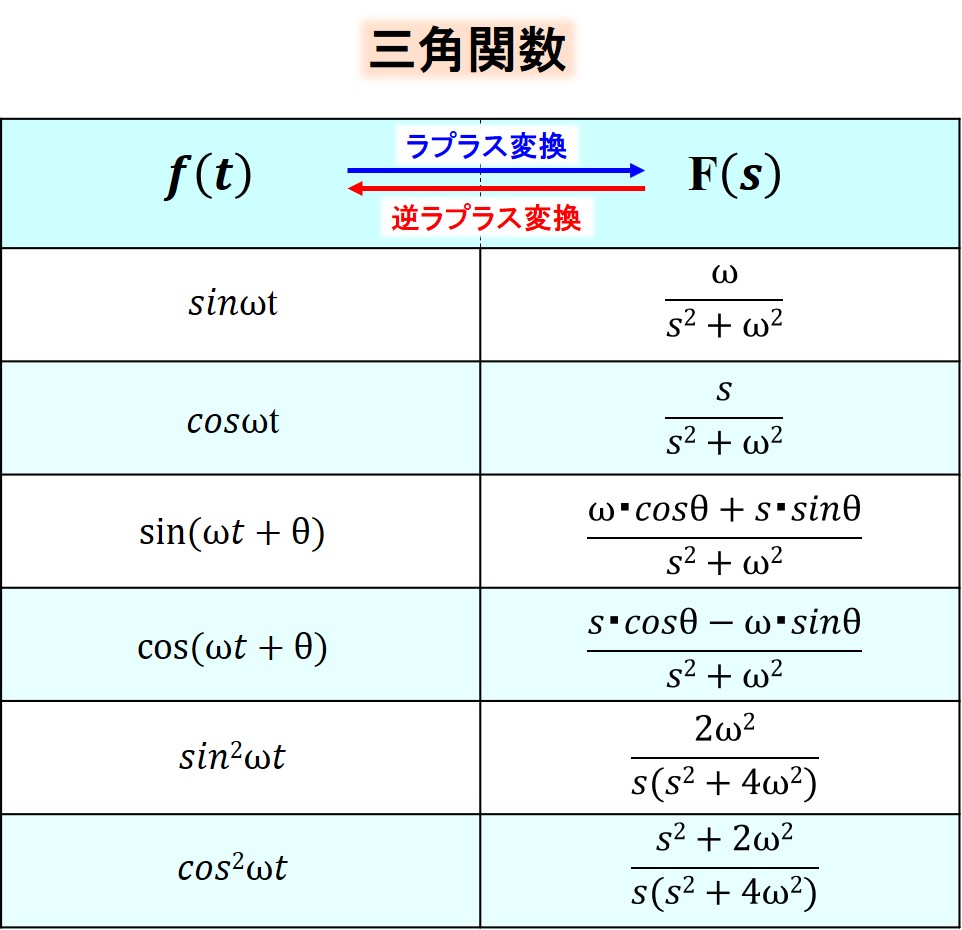
指数関数・tと指数関数、三角関数の積

指数関数と三角関数の積

双曲線関数

重要な関数のラプラス変換の導出
導出の際には、基本的に部分積分を使って計算していきます。
\(t\)の\(n\)乗の計算
まずは、定数\(A\)と\(t\)の\(n\)乗の計算です。
\(n\)乗は1乗と2乗の計算を示します。

三角関数の計算
\(sin\)と\(cos\)の計算を示します。
この計算にはオイラーの公式を利用して解きます。
\(f(t)=Asinωt\)

\(f(t)=Acosωt\)
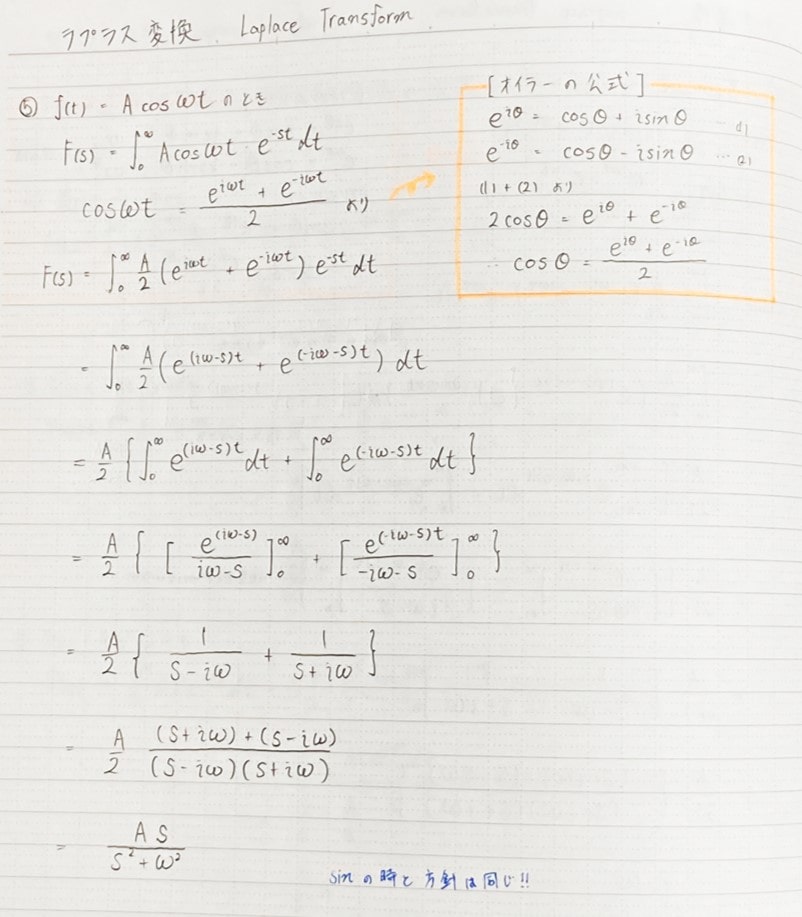
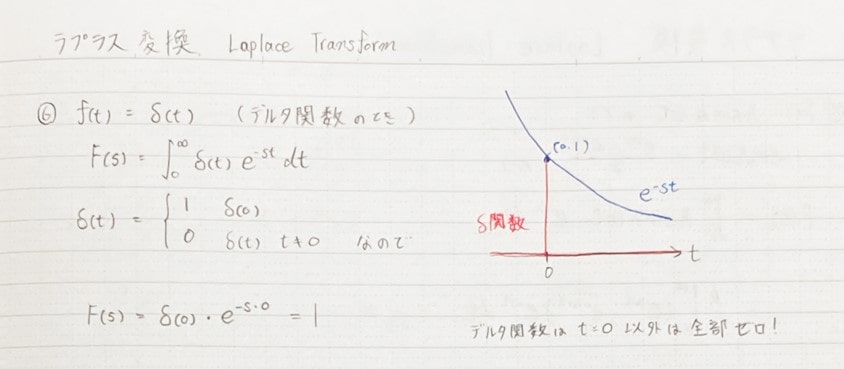
δ関数の計算
δ関数のラプラス変換です。
δ関数は\(t=0\)のときだけ1となり、ほかの\(t\)の値では0となりますので、\(t=0\)のときだけを考えればよいので簡単です。
双曲線関数の計算
\(sinh\)と\(cosh\)の計算結果を示します。
双曲線関数\(sinh\)や\(cosh\)は定義からeの関数で表すことができますので、指数関数の形で計算します。
\(f(t)=Asinhωt\)

\(f(t)=Acoshωt\)
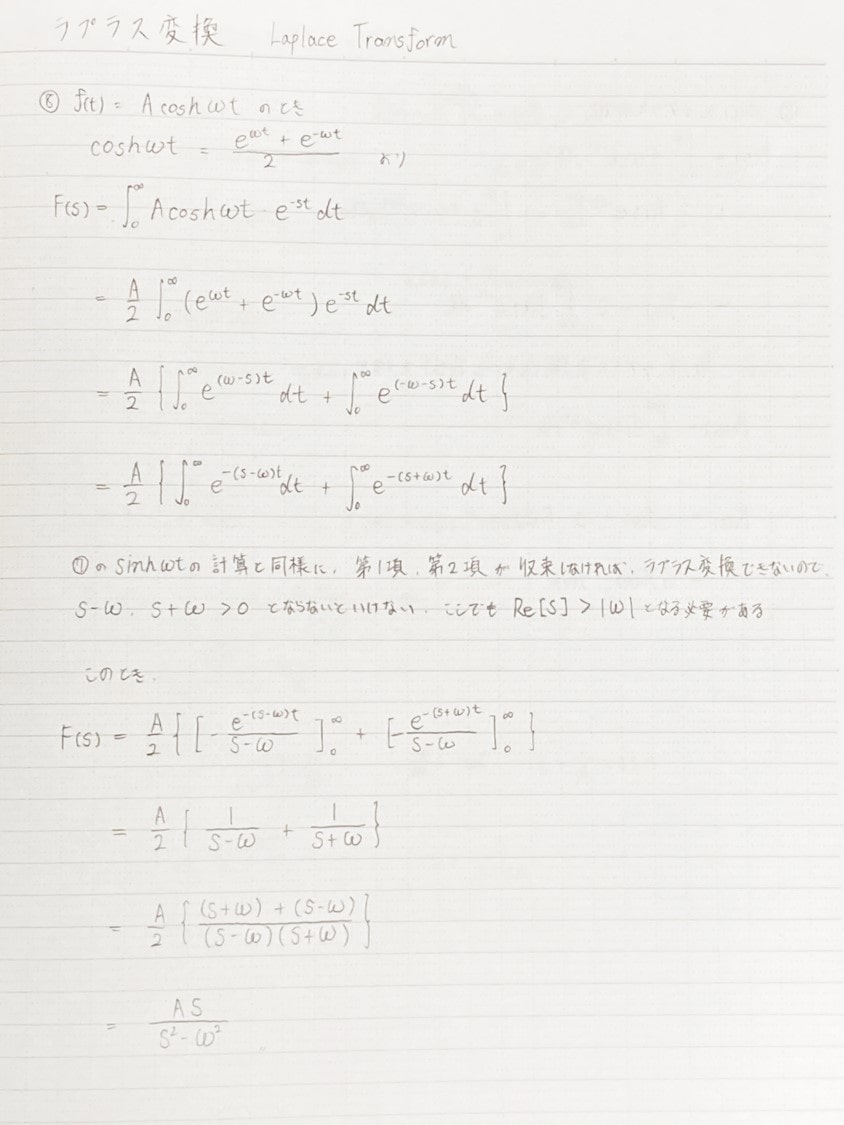
まとめ
今回はラプラス変換表の紹介をしました。
いちいちラプラス変換の結果を覚えてられない人は、ラプラス変換表を使って計算することになります。
大学のテストなどでは、簡単なラプラス変換をやらなければいけない可能性もありますので、しっかりと計算できるようにしておきましょう。
