
せん断力と曲げモーメントが微積の関係にあるって聞いたんだけど、どういうこと??
本日はそんな疑問にお答えします。
結論的には、下の表に示すように、外力、せん断力、曲げモーメント、たわみ角、たわみ量は全て微分、積分の関係にあります。
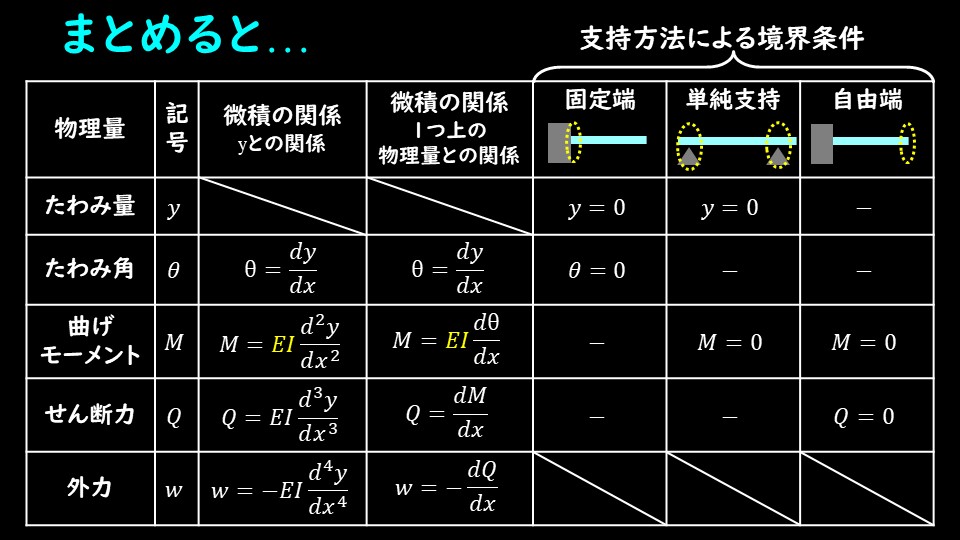
本記事では、外力、せん断力、曲げモーメントが微積分の関係にあることの証明をします。
動画でも解説していますので、参考にしていただければと思います。
モデル
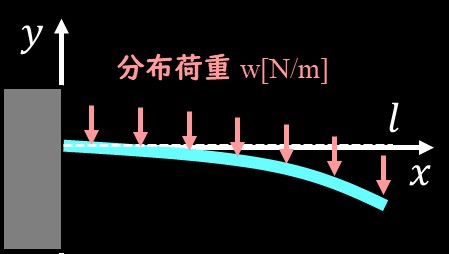
上図のような片持ち梁の等分布荷重を考えてみましょう。
この分布荷重が作用している微小領域を拡大し、力のつりあい、モーメントのつり合いを考えていきます。
力のつり合い
まずは微小領域に作用している外力を考えましょう。
微小領域の長さを\(dx\)とすると、分布荷重\(w(x)\)が作用しているので、\(wdx\)の荷重が作用していることになります。
この外力だけだと、この微小領域は下向きに飛んでいってしまうので、内力としてせん断力を考える必要があります。
左側に作用しているせん断力を\(Q\)とすると、右側の面に作用しているせん断力は\(dQ\)だけ変化したと考えて、\(Q+dQ\)と書くことができます。
これらの力のつり合いを考えると、
$$wdx-Q+Q+dQ=0$$
式を整理すると
$$w=-\frac{dQ}{dx}$$
となります。
このようにせん断力\(Q\)を微分すると、外力となることがわかります。
モーメントのつり合い
さて、それでは次にモーメントのつり合いを考えてみましょう。
微小領域の左側を支点に、モーメントのつり合いを考えます。
まず、外力によるモーメントですが、外力が作用している点は、微小領域中央とみなすことができるので、
$$M_P=wdx\frac{dx}{2}$$
となります。
次に、せん断力によるモーメントですが、左側の面は支点からの距離がゼロなので、ゼロとなります。
右側のせん断力によるモーメントですが、せん断力×距離で\((Q+dQ)dx\)となりますね。
最後に曲げモーメントとして、左側に\(M\)、右側に\(M+dM\)を付け加えて、モーメントのつり合いを考えます。
$$-wdx\frac{dx}{2}-(Q+dQ)dx-M+M+dM=0$$
ここで\(dQ=-wdx\)なので、
$$-Qdx+w\frac{dx^2}{2}+dM=0$$
と整理できます。\(dx\)は微小量なので、\(dx^2<<1\)となって、
$$-Qdx+dM=0$$
となります。式を整理すると、
$$Q=\frac{dM}{dx}$$
となり、せん断力は曲げモーメントを微分したもの、という式が導出されます。
以上で証明は終わりです。
曲げモーメントからたわみの式を導出する過程は過去の記事で紹介していますので、そちらを参考にしていただければと思います。
その結果を用いると、曲げモーメントは下記のように表すことができます。
$$M=EI\frac{d^2y}{dx^2}=EI\frac{dθ}{dx}$$
\(E\)はヤング率、\(I\)は断面2次モーメント、\(θ\)はたわみ角で、
$$θ=\frac{dy}{dx}$$
でしたね。材料力学では\(θ\)が非常に小さいと仮定して進めるので、上記のような関係式が成り立つわけです。
これらをまとめると、冒頭で示した表を得ることができます。
まとめ
材料力学の曲げ変形における、外力、せん断力、曲げモーメントが微積分で繋がっていることを説明させていただきました。
検算などにも使える非常に便利な関係ですので、覚えておくことをおすすめします。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
